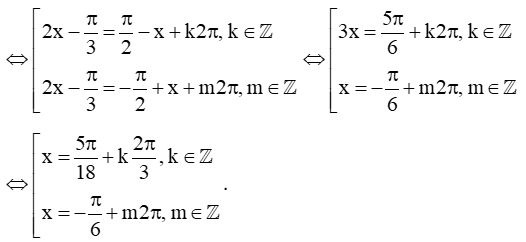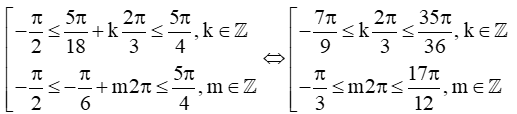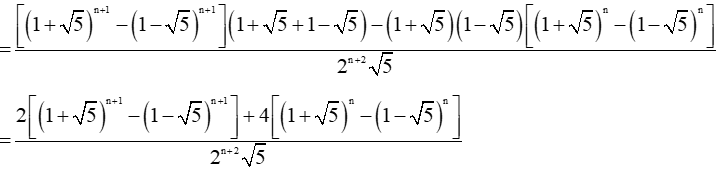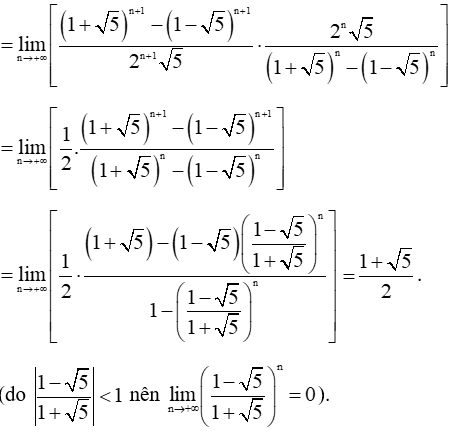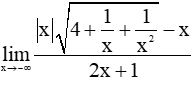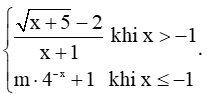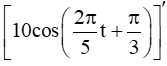Sách bài tập Toán lớp 11 Bài tập ôn tập cuối năm
A – Trắc nghiệm
Bài 1 trang 66 SBT Toán 11 Tập 2: Khẳng định nào sau đây là sai?
A. sinx - cosx = √2sin(x-π4).
B. sinx + cosx = √2sin(x+π4).
C. sinx + cosx = √2cos(x+π4).
D. cosx - sinx = √2cos(x-π4).
Lời giải:
Đáp án đúng là: C
sinx + cosx = √2(√22⋅sinx+√22⋅cosx) = √2(cosx⋅cosπ4+sinx⋅sinπ4)
= √2cos(x-π4). Vậy khẳng định C sai.
Bài 2 trang 66 SBT Toán 11 Tập 2: Hàm số y = cos2x3 là hàm số tuần hoàn với chu kì
A. 2π.
B. π.
C. 3π2.
D. 3π.
Lời giải:
Đáp án đúng là: D
Hàm số y = cos2x3 tuần hoàn với chu kì T=2π23=3π .
A. −π6 .
B. 5π6 .
C. 5π18 .
D. 17π18.
Lời giải:
Đáp án đúng là: D
Ta có cos(2x−π3)=sinx⇔cos(2x−π3)=cos(π2−x)
Có 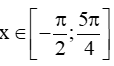
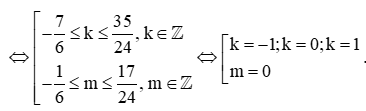
Với k = −1 thì x=−7π18 ;
Với k = 0 thì x=5π18 ;
Với k = 1 thì x=17π18 ;
Với m = 0 thì x=−π6 .
Vậy x=17π18 là nghiệm lớn nhất cần tìm.
A. −197.
B. −199.
C. −170.
D. 289.
Lời giải:
Đáp án đúng là: A
Vì u10 = u1 + 9d nên −17 = 1 + 9d ⇔ d = −2.
Số hạng thứ 100 của cấp số cộng là u100 = u1 + 99d = 1 + 99.(−2) = −197.
A. 1 536.
B. −1 536.
C. 3 072.
D. −3 072.
Lời giải:
Đáp án đúng là: B
Có u5 = u1.q4 = 48; u12 = u1.q11 = −6 144.
Do đó u5u12=q4q11=48−6144⇒1q7=−1128⇒q7 = -128 ⇒q = -2 .
Mà u5 = u1×q4 = 48 nên u1=48(−2)4=3.
Khi đó số hạng thứ mười của cấp số nhân là u10 = u1.q9 = 3.(−2)9 = −1 536.
A. 129 .
B. 119 .
C. 109 .
D. 2218 .
Lời giải:
Đáp án đúng là: B
Ta có x = 1,2222… = 1+210+2100+21000+...
Ta thấy 210+2100+21000+... là tổng cấp số nhân lùi vô hạn với u1=210;q=110 .
Do đó 210+2100+21000+...=2101−110=29 .
Vậy x = 1,2222…=1+210+2100+21000+...=1+29=119.
Bài 7 trang 67 SBT Toán 11 Tập 2: Trong các mệnh đề sau, mệnh đề sai là
A. limx→0−1x=−∞ .
B. limx→0+1x=+∞ .
C. limx→0−1x2=−∞ .
D. limx→0+13√x=+∞ .
Lời giải:
Đáp án đúng là: C
Ta có limx→0−1x2=+∞ nên đáp án C sai.
Bài 8 trang 67 SBT Toán 11 Tập 2: Giá trị của m để hàm số 
A. 3.
B. 1.
C. −3.
D. −1.
Lời giải:
Đáp án đúng là: D
+) Khi x > −1 thì f(x)=x2+3x+2x+1 liên tục.
+) Khi x < −1 thì f(x) = −2x + m liên tục.
Do đó hàm số liên tục trên ℝ khi và chỉ khi hàm số liên tục tại x = −1.
Ta xét tính liên tục của hàm số tại x = −1. Ta có:
f(– 1) = 2 + m;
limx→(−1)−f(x)=limx→(−1)−(−2x+m)=2+m;
limx→(−1)+f(x)=limx→(−1)+x2+3x+2x+1=limx→(−1)+(x+1)(x+2)x+1=limx→(−1)+(x+2)=1.
Để hàm số liên tục tại x = −1 khi và chỉ khi 2 + m = 1 ⇔ m = −1.
Vậy m = −1 là giá trị cần tìm.
Bài 9 trang 67 SBT Toán 11 Tập 2: Hàm số đồng biến trên toàn bộ tập số thực ℝ là
A. y = 2−x.
B. y=(πe)x .
C. y = lnx.
D. y = logx.
Lời giải:
Đáp án đúng là: B
+) Hàm số y = 2−x = (12)x có 0<12<1 nên hàm số y = 2−x nghịch biến trên ℝ.
+) Hàm số y=(πe)x có πe>1 nên hàm số y=(πe)x đồng biến trên ℝ.
+) Hàm số y = lnx đồng biến trên (0; +∞).
+) Hàm số y = logx đồng biến trên (0; +∞).
Bài 10 trang 67 SBT Toán 11 Tập 2: Tập nghiệm của bất phương trình (12)2x2−x+1≤(14)x là
A. 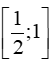
B. 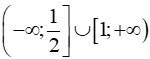
C. (12;1) .
D. (−∞;12)∪(1;+∞) .
Lời giải:
Đáp án đúng là: B
Ta có (12)2x2−x+1≤(14)x⇔(12)2x2−x+1≤(12)2x
⇔ 2x2 – x + 1 ≥ 2x ⇔ 2x2 – 3x + 1≥0
⇔ (2x – 1)(x – 1) ≥ 0 ⇔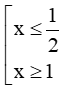
Vậy tập nghiệm của bất phương trình là 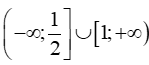
Bài 11 trang 68 SBT Toán 11 Tập 2: Đạo hàm của hàm số y=sin22x+ex2−1 là
A. y' .
B. y' = 2sin2x + 2x.
C. y' = 2sin4x + 2x .
D. y' = 4sin2xcos2x + .
Lời giải:
Đáp án đúng là: C
Ta có
= 2sin2x(sin2x)' + (x2 - 1)'
= 4sin2xcos2x + 2x = 2sin4x + 2.
Vậy y' = 2sin4x + 2x.
A. Gia tốc của chuyển động tại thời điểm t = 2 giây là a = 0 m/s2.
B. Vận tốc của chuyển động tại thời điểm t = 2 giây là v = −4 m/s.
C. Gia tốc của chuyển động tại thời điểm t = 3 giây là a = 12 m/s2.
D. Vận tốc của chuyển động tại thời điểm t = 3 giây là v = 0 m/s.
Lời giải:
Đáp án đúng là: C
Vận tốc của chuyển động tại thời điểm t là v(t) = s'(t) = 3t2 – 6t.
Gia tốc của chuyển động tại thời điểm t là a(t) = v'(t) = 6t – 6.
Khi đó vận tốc của chuyển động tại thời điểm t = 2 giây là v(2) = 3.22 – 6.2 = 0 m/s.
Gia tốc của chuyển động tại thời điểm t = 2 giây là a(2) = 6.2 – 6 = 6 m/s2.
Vận tốc của chuyển động tại thời điểm t = 3 giây là v(3) = 3.32 – 6.3 = 9 m/s.
Gia tốc của chuyển động tại thời điểm t = 3 giây là a(3) = 6.3 – 6 = 12 m/s2.
|
Thời gian (giờ) |
[0; 0,5) |
[0,5; 1) |
[1; 1,5) |
[1,5; 2) |
[2; 2,5) |
|
Số học sinh |
2 |
5 |
8 |
6 |
4 |
Thời gian (giờ) sử dụng mạng xã hội trung bình trong ngày của nhóm học sinh là
A. 1,0.
B. 1,25.
C. 1,35.
D. 1,5.
Lời giải:
Đáp án đúng là: C
Ta có cỡ mẫu n = 2 + 5 + 8 + 6 + 4 = 25.
Nhóm [0; 0,5) có giá trị đại diện là ;
Nhóm [0,5; 1) có giá trị đại diện là ;
Nhóm [1; 1,5) có giá trị đại diện là ;
Nhóm [1,5; 2) có giá trị đại diện là ;
Nhóm [2; 2,5) có giá trị đại diện là .
Thời gian sử dụng mạng xã hội trung bình trong ngày của nhóm học sinh là
(giờ).
Vậy thời gian sử dụng mạng xã hội trung bình trong ngày của nhóm học sinh là 1,35 giờ.
|
Thời gian (giờ) |
[0; 0,5) |
[0,5; 1) |
[1; 1,5) |
[1,5; 2) |
[2; 2,5) |
|
Số học sinh |
2 |
5 |
8 |
6 |
4 |
Nhóm chứa tứ phân vị thứ ba là nhóm
A. [0,5; 1).
B. [1; 1,5).
C. [1,5; 2).
D. [2; 2,5).
Lời giải:
Đáp án đúng là: C
Có cỡ mẫu n = 2 + 5 + 8 + 6 + 4 = 25.
Giả sử x1; x2; …; x25 là mẫu số liệu đã được xếp theo thứ tự không giảm.
Tứ phân vị thứ ba .
Do x19; x20 đều thuộc nhóm [1,5; 2) nên nhóm [1,5; 2) chứa Q3.
A. 14%.
B. 15%.
C. 13%.
D. 14,5%.
Lời giải:
Đáp án đúng là: A
Gọi biến cố A: “Học sinh học giỏi môn Ngữ văn”;
B: “Học sinh học giỏi môn Toán”;
AB: “Học sinh học giỏi cả hai môn”;
A B: “Học sinh học giỏi môn Ngữ Văn hoặc học giỏi môn Toán”.
Theo đề, có P(A) = 9%; P(B) = 12%; P(AB) = 7%.
Có P(A È B) = P(A) + P(B) – P(AB) = 9% + 12% − 7% = 14%.
Vậy tỉ lệ học sinh tỉnh X học giỏi môn Ngữ văn hoặc học giỏi môn Toán là 14%.
A. .
B. .
C. .
D. .
Lời giải:
Đáp án đúng là: B
Gọi biến cố A: “An lấy được viên bi xanh từ hộp I”;
B: “Bình lấy được viên bi đỏ từ hộp II”;
C: “Hai viên bi lấy ra có màu khác nhau”.
Khi đó C = AB.
Theo đề, ta suy ra P(A) = ; P() = 1- = ; P(B) = ; P() = 1- = .
Vì A, B độc lập nên , cũng độc lập.
Do đó P(C) = P(AB) = P(AB) + P()
= P(A).P(B)+P().P() = .
Vậy xác suất để hai viên bi lấy ra có màu khác nhau là .
A. .
B. .
C. .
D. .
Lời giải:
Đáp án đúng là: C
Xác suất để cả 4 đồng xu đều xuất hiện mặt ngửa là .
A. 60°.
B. 90°.
C. 150°.
D. 30°.
Lời giải:
Đáp án đúng là: B
Có 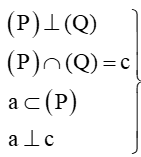
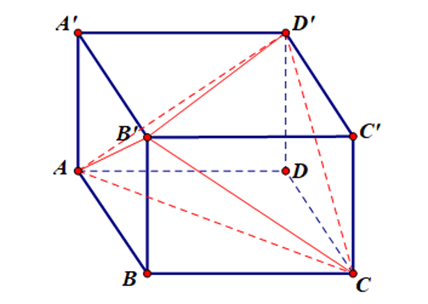
A. 90°.
B. 30°.
C. 60°.
D. 45°.
Lời giải:
Đáp án đúng là: C
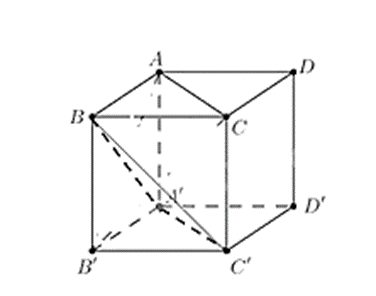
Vì ABCD.A'B'C'D' là hình lập phương nên các mặt là hình vuông.
Có AA' // CC' và AA' = CC' (vì chúng cùng song song và bằng BB') nên ACC'A' là hình bình hành, suy ra AC // A'C'.
Khi đó góc giữa hai đường thẳng AC và BC' bằng góc giữa hai đường thẳng A'C' và BC', mà (A'C', BC') = .
Xét tam giác BB'C' vuông tại B', có .
Xét tam giác A'B'C' vuông tại B', có .
Xét tam giác BB'A' vuông tại B', có .
Xét tam giác A'BC' có A'B = BC' = A'C' = a nên tam giác A'BC' đều, suy ra .
Vậy góc giữa hai đường thẳng AC và BC' bằng 60°.
A. .
B. .
C. .
D. .
Lời giải:
Đáp án đúng là: E. .
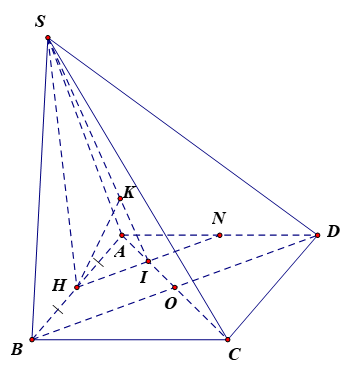
Vì tam giác SAB đều, H là trung điểm của AB nên SH là đường cao hay SH AB.
Do (SAB) (ABCD); (SAB) (ABCD) = AB mà SH AB nên SH (ABCD), suy ra SH AC.
Gọi N là trung điểm của AD.
Xét tam giác ABD có H là trung điểm của AB, N là trung điểm của AD nên HN là đường trung bình của tam giác ABD, suy ra HN // BD.
Do ABCD là hình vuông nên AC BD mà HN // BD nên HN AC.
Vì HN AC và SH AC nên AC (SHN), suy ra (SAC) (SHN).
Gọi AC HN = I, kẻ HK SI tại K.
Vì (SAC) (SHN), (SAC) (SHN) = SI mà HK SI nên HK (SAC).
Do đó d(H, (SAC)) = HK.
Gọi O là giao điểm của AC và BD.
Vì ABCD là hình vuông nên O là trung điểm của BD.
Xét tam giác ABD vuông tại A, có .
Vì O là trung điểm của BD nên BO = = .
Xét tam giác ABO có H là trung điểm của AB, HI // BO (do HN //BD) nên I là trung điểm của AO.
Vì I là trung điểm của AO, H là trung điểm của AB nên HI là đường trung bình của tam giác ABO, suy ra .
Vì tam giác SAB là tam giác đều cạnh a, SH là đường cao nên .
Vì SH (ABCD) nên SH HI hay tam giác SHI vuông tại H.
Xét tam giác SHI vuông tại H, HK là đường cao, có:
.
Vậy d(H, (SAC)) = .
A. .
B. .
C. .
D. .
Lời giải:
Đáp án đúng là: A
Gọi O là giao điểm của AC, BD.
Vì S.ABCD là hình chóp đều nên SO (ABCD), suy ra SO BD.
Do ABCD là hình vuông nên AC BD.
Vì SO BD và AC BD nên BD (SAC).
Kẻ OE SC tại E. Vì BD (SAC) nên BD OE. Do đó d(BD, SC) = OE.
Xét tam giác ABC vuông tại B, có .
Vì ABCD là hình vuông nên O là trung điểm của AC, suy ra AO = OC = = .
Vì SO (ABCD) nên SO AC.
Xét tam giác SOA vuông tại O, có SO = .
Xét tam giác SOC vuông tại O, có
.
Vậy d(BD, SC) = .
A. .
B. .
C. .
D. .
Lời giải:
Đáp án đúng là: B
Gọi O là tâm của tam giác A'B'C'.
Do AA'B'C' là hình tứ diện đều nên O là trọng tâm đồng thời là trực tâm của tam giác A'B'C' và AO (A'B'C').
Gọi A'O B'C' = H, suy ra A'H B'C'.
Xét tam giác A'B'C' đều cạnh a, A'H là đường cao nên A'H = , .
Vì A'O = A'H nên A'O = .
Vì AO (A'B'C') nên AO A'O hay tam giác AA'O vuông tại O.
Xét tam giác AA'O vuông tại O, có AO = .
Khi đó .
Vậy .
A. .
B. .
C. .
D. .
Lời giải:
Đáp án đúng là: A
Ta có VACB'D' = VABCD.A'B'C'D' – VA.A'B'D' – VB'.ABC – VC.C'D'B' – VD'.DAC.
Vì hình chữ nhật ABCD có AB = AD = a nên ABCD là hình vuông.
Do đó ABCD.A'B'C'D' là hình hộp chữ nhật có đáy là hình vuông.
Do A'B'C'D' là hình vuông nên SA'B'D' = SB'C'D' = .
Do ABCD là hình vuông nên SABC = SADC = .
Có VA.A'B'D' .
VB'.ABC .
VC.C'D'B' .
VD'.DAC .
VABCD.A'B'C'D' = AA'.AB.AD = a.a.a = a3.
Khi đó:
VACB'D' = VABCD.A'B'C'D' – VA.A'B'D' – VB'.ABC – VC.C'D'B' – VD'.DAC .
Vậy VACB'D .
A. .
B. .
C. .
D. .
Lời giải:
Đáp án đúng là: D
Gọi M là trung điểm của BC, suy ra AM là trung tuyến.
Do ABC là tam giác đều có AM là trung tuyến nên AM đồng thời là đường cao hay AM BC.
Vì SA (ABC) nên SA AM.
Do AM BC và SA AM nên d(SA, BC) = AM.
Vì ABC là tam giác đều có AM là đường cao nên AM = .
Vậy d(SA, BC) = .
B – Tự luận
Bài 25 trang 70 SBT Toán 11 Tập 2: Cho sinx = -, x . Tính giá trị cos.
Lời giải:
Có sin2x + cos2x = 1 nên .
Mà nên cosx < 0. Do đó cosx = -.
Lại có cos = cos2xcos+sin2xsin
= cos2x+sin2x
= (1-2sin2x) + sinxcosx
.
Vậy .
Bài 26 trang 70 SBT Toán 11 Tập 2: Chứng minh rằng:
a) sin3x = 4sinx sin(60° − x) sin(60° + x);
Lời giải:
a) Có sin(60° − x) sin(60° + x) = -(cos120o - cos(-2x))
= - = cos2x.
Do đó 4sinx sin(60° − x) sin(60° + x) = 4sinx = sinx + 2sinxcos2x
= sinx + sin3x + sin(−x) = sinx + sin3x – sinx = sin3x.
Vậy sin3x = 4sinx sin(60° − x) sin(60° + x).
b) Vế phải =
= tan2x = vế trái.
Vậy = tan2x.
a) un = 5n – 7; b) un = 9.2n; c) un = n2 – n + 1.
Lời giải:
a) + Có un + 1 = 5(n + 1) – 7 = 5n – 2.
Xét un + 1 – un = 5n – 2 – (5n – 7) = 5 với mọi n.
Do đó (un) là cấp số cộng với u1 = −2 và d = 5.
+ Có u1 = −2; u2 = 3; u3 = 8.
Vì nên (un) không là cấp số nhân.
b) + Có un + 1 = 9.2n + 1 = 18.2n.
Vì với mọi n nên (un) là cấp số nhân.
+ Có u1 = 18; u2 = 36; u3 = 72.
Vì u2 – u1 = 36 – 18 = 18 ≠ u3 – u2 = 72 – 36 = 36 nên (un) không là cấp số cộng.
c) Có u1 = 1; u2 = 3; u3 = 7.
Vì u2 – u1 = 3 – 1 ≠ u3 – u2 = 7 – 3 nên (un) không là cấp số cộng.
Vì nên (un) không là cấp số nhân.
Lời giải:
Ta có 5 năm là 20 quý.
Phương án 1: Ta thấy (un) là cấp số cộng với u1 = 64,5 và d = 10.
Tổng số tiền lương kĩ sư nhận được sau 5 năm là:
= 3 190 (triệu đồng).
Phương án 2: Ta thấy (un) là cấp số nhân với u1 = 24 và q = 1,2.
Tổng số tiền lương kĩ sư nhận được sau 5 năm là:
4 480,5 (triệu đồng).
Vậy kĩ sư nên chọn phương án nhận lương thứ 2.
Bài 29 trang 70 SBT Toán 11 Tập 2: Giả sử un là số hạng thứ n của dãy số (un) và .
b) Viết 11 số hạng đầu tiên của dãy Fibonacci và 10 tỉ số đầu tiên.
Lời giải:
a) Ta có an + 2 – bn + 2 = an + 1.a − bn + 1.b
= an + 1.a + an + 1.b − bn + 1.b − bn + 1.a − an + 1.b + bn + 1.a
= an + 1.(a + b) − bn + 1.(a + b) – ab(an − bn)
= (an + 1 − bn + 1).(a + b) – ab(an − bn) (*)
Có .
.
Áp dụng (*), ta có:
= un+1 + un.
Vậy un + 2 = un+1 + un. Do đó (un) là dãy Fibonacci.
b) Ta có bảng sau
|
n |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
|
un |
1 |
1 |
2 |
3 |
5 |
8 |
13 |
21 |
34 |
55 |
89 |
|
1 |
2 |
Ta có
Bài 30 trang 70 SBT Toán 11 Tập 2: Tính các giới hạn sau:
Lời giải:
a) (2x-5) = -9.
b) =
.
c) .
(do (x-4) = -2 < 0 và (x-2)2 = 0, (x-2)2>0, 2).
d) (do (2x) = -10 < 0 và (x+5) = 0, x + 5 < 0, ∀x < −5).
Bài 31 trang 71 SBT Toán 11 Tập 2: Tìm m để hàm số sau liên tục trên toàn bộ tập số thực ℝ:
f(x) =
Lời giải:
+) Với x > −1 thì f(x) = liên tục.
+) Với x < −1 thì f(x) = m.4−x + 1 liên tục.
Để hàm số liên tục trên toàn bộ tập số thực ℝ khi và chỉ khi hàm số liên tục tại x = −1.
Ta xét tính liên tục của hàm số tại x = −1. Ta có:
f(– 1) = 4m + 1;
;
.
Suy ra hàm số liên tục trên ℝ khi và chỉ khi 4m+1 = m = -.
Vậy m = - là giá trị cần tìm.
Bài 32 trang 71 SBT Toán 11 Tập 2: Giải các phương trình sau:
b) log3(x2 – x – 3) = log3(2x – 1) + 1.
Lời giải:
a) x2 – 3x = log344x x2 – 3x = 4xlog34 x2 – 3x − 4xlog34 = 0
x(x – 3 − 4log34) = 0 x = 0 hoặc x = 3 + 4log34.
Vậy tập nghiệm của phương trình là S = {0; 3 + 4log34}.
b) Điều kiện 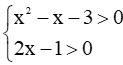
Ta có log3(x2 – x – 3) = log3(2x – 1) + 1
log3(x2 – x – 3) = log3(2x – 1) + log33
log3(x2 – x – 3) = log3[3(2x – 1)]
log3(x2 – x – 3) = log3(6x – 3)
x2 – x – 3 = 6x – 3 x2 – 7x = 0
x(x – 7) = 0 x = 0 hoặc x = 7.
Đối chiếu với điều kiện thì x = 7 thỏa mãn điều kiện.
Vậy nghiệm của phương trình là x = 7.
Lời giải:
Có f'(x) = (32x −1)' = (32x −1).ln3.(2x – 1)' = 2.ln3.32x −1.
g'(x) = (xln9)' = ln9.
Để f'(x) < g'(x) thì 2.ln3.32x −1 < ln9 2.ln3.32x −1 < ln32 2.ln3.32x −1 < 2.ln3
32x −1 < 1 2x – 1 < 0 x < .
Vậy nghiệm của bất phương trình là: x < .
Bài 34 trang 71 SBT Toán 11 Tập 2: Tính đạo hàm của các hàm số sau:
Lời giải:
a)
.
Vậy .
b)
Vậy .
Lời giải:
Giả sử hoành độ của điểm M là x0.
Vì tiếp tuyến của đồ thị hàm số y = 2x3 – 3x2 – 11x + 13 tại điểm M có hệ số góc là 1 nên y'(x0) = hoặc .
Với x0 = 2 thì y0 = −5; với x0 = −1 thì y0 = 19.
Vậy M(2; −5) hoặc M(−1; 19) là điểm cần tìm.
a) Tìm thời điểm đầu tiên để vật có li độ lớn nhất.
b) Tìm thời điểm đầu tiên để vật có vận tốc bằng 0.
c) Tìm thời điểm đầu tiên để vật có gia tốc bằng 0.
Lời giải:
a) Vì với mọi t.
Do đó, vật có li độ lớn nhất khi
.
Do t 0 nên thời điểm đầu tiên vật có li độ lớn nhất tương ứng với k = 1, tức là tại thời điểm (giây).
Vậy thời điểm đầu tiên vật có li độ lớn nhất là giây.
b) Ta có v(t) = x'(t) =
.
Vận tốc bằng 0 tức là
.
Do t 0 nên thời điểm đầu tiên vật có vận tốc bằng 0 tương ứng với k = 1, tức là tại thời điểm (giây).
Vậy thời điểm đầu tiên để vật có vận tốc bằng 0 là giây.
c) Ta có a(t) = v'(t) =
.
Gia tốc bằng 0 tức là
.
Do t 0 nên thời điểm đầu tiên vật có gia tốc bằng 0 tương ứng với k = 0, tức là tại thời điểm (giây).
Vậy thời điểm đầu tiên để vật có gia tốc bằng 0 là giây.
|
Mức giá (triệu đồng/m2) |
[10; 15) |
[15; 20) |
[20; 25) |
[25; 30) |
[30; 35) |
|
Số khách hàng |
15 |
25 |
38 |
29 |
13 |
a) Ước lượng mức giá có nhiều khách hàng lựa chọn nhất.
Lời giải:
a) Tổng số khách hàng là n = 15 + 25 + 38 + 29 + 13 = 120.
Nhóm chứa mốt là nhóm [20; 25) (vì nhóm này có tần số lớn nhất).
Ta có a3 = 20; m3 = 38; m2 = 25; m4 = 29, h = 5.
Áp dụng công thức tính Mo, ta được:
.
Vậy mức giá có nhiều khách lựa chọn nhất khoảng 22,95 triệu đồng/m2.
b) Nhóm chứa tứ phân vị thứ ba là nhóm [25; 30).
Ta có a4 = 25; a5 = 30; m1 = 15; m2 = 25; m3 = 38; m4 = 29.
Áp dụng công thức tính tứ phân vị thứ ba Q3, ta được:
.
Vậy công ty nên tập trung vào các bất động sản có mức giá ít nhất khoảng 27,07 triệu đồng/m2.
A: “Có ít nhất một xúc xắc xuất hiện mặt 6 chấm”.
B: “Tổng số chấm xuất hiện trên mặt của hai xúc xắc bằng 7”.
b) Hai biến cố A và B có độc lập hay không?
Lời giải:
a) Gọi A1 là biến cố: “Xúc xắc I ra mặt 6 chấm”, A2 là biến cố: “Xúc xắc II ra mặt 6 chấm”.
là biến cố: “Cả hai con xúc xắc đều không ra mặt 6 chấm”.
Khi đó A = A1 A2 và P(A) = 1-P() = 1 - P().P() = (do A1; A2 độc lập nên ; độc lập).
Theo đề có P(A1) = ; P(A2) = , suy ra P() = ; P() = .
Có P().P() = .
Do đó P(A) = 1-P() = .
B: “Tổng số chấm xuất hiện trên mặt của hai xúc xắc bằng 7”.
Các kết quả thuận lợi cho biến cố B là: (1, 6); (2, 5); (3, 4); (4, 3); (5, 2); (6, 1).
Do đó P(B) = .
Vậy .
b) AB là biến cố: “Tổng số chấm xuất hiện trên mặt của hai xúc xắc bằng 7 trong đó ít nhất có một xúc xắc xuất hiện mặt 6 chấm”.
Các kết quả thuận lợi cho biến cố AB là (6, 1); (1, 6).
Do đó . Lại có P(A).P(B) = .
Do P(AB) ≠ P(A).P(B) nên A, B không độc lập.
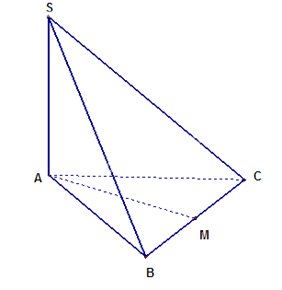
b) Tính góc giữa đường thẳng SC và mặt phẳng (ABCD).
c) Tính theo a khoảng cách từ điểm A đến mặt phẳng (SBC).
Lời giải:
a) Do ABCD là hình vuông nên BC AB
Mà SA BC (do SA (ABCD)) nên BC (SAB), suy ra (SBC) (SAB).
b) Vì SA (ABCD) nên AC là hình chiếu của SC trên mặt phẳng (ABCD).
Do đó, góc giữa đường thẳng SC và mặt phẳng (ABCD) bằng góc giữa hai đường thẳng SC và AC, mà (SC, AC) = .
Xét tam giác ABC vuông tại B, có AC = .
Vì SA (ABCD) nên SA AC hay tam giác SAC vuông tại A.
Xét tam giác SAC vuông tại A, có AC = SA = a nên tam giác SAC vuông cân tại A, suy ra .
Vậy góc giữa đường thẳng SC và mặt phẳng (ABCD) bằng 45°.
c) Kẻ AH SB tại H.
Vì (SBC) (SAB), (SBC) (SAB) = SB mà AH SB nên AH (SBC).
Khi đó d(A, (SBC)) = AH.
Vì SA (ABCD) nên SA AB hay tam giác SAB vuông tại A.
Xét tam giác SAB vuông tại A, AH là đường cao, có:
.
Vậy d(A, (SBC)) = .
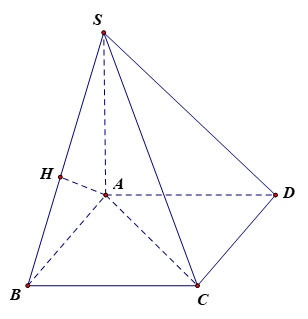
a) Tính theo a thể tích khối chóp S.ABCD.
b) Tính theo a khoảng cách giữa hai đường thẳng AD và SB.
Lời giải:
a) Gọi O là giao điểm của AC và BD, suy ra O là trung điểm của AC, BD.
Vì S.ABCD là hình chóp đều nên SO (ABCD).
Xét tam giác vuông ABC vuông tại B, có AC = .
Vì O là trung điểm của AC nên AO = OC = .
Vì SO (ABCD) nên SO AC.
Xét tam giác SOA vuông tại O, có SO = .
Khi đó .
Vậy .
b) Có ABCD là hình vuông nên AD // BC suy ra AD // (SBC).
Khi đó d(AD, SB) = d(AD, (SBC)) = d(A, (SBC)).
Đường thẳng AO cắt mặt phẳng (SBC) tại C và O là trung điểm của AC nên
d(A, (SBC)) = 2d(O, (SBC)).
Kẻ OM BC tại M, OH SM tại H.
Vì BC OM, BC SO (do SO (ABCD)) nên BC (SOM), suy ra (SBC) (SOM).
Mà OH SM nên OH (SBC). Do đó d(O, (SBC)) = OH.
Có OM // AB (vì cùng vuông góc với BC).
Xét tam giác ABC có O là trung điểm của AC, OM // AB nên M là trung điểm của BC, suy ra OM là đường trung bình. Do đó OM = .
Vì SO (ABCD) nên SO OM hay tam giác SOM vuông tại O.
Xét tam giác SOM vuông tại O, OH là đường cao có:
.
Vậy d(AD, SB) = 2OH = .
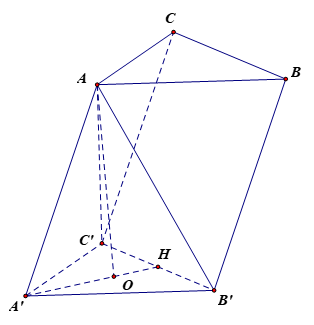
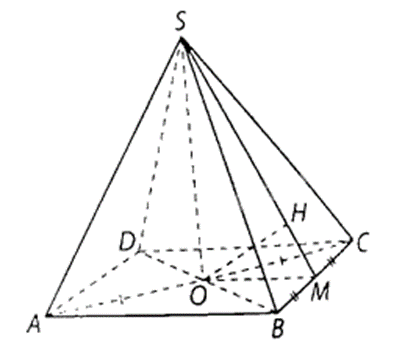
a) Chứng minh rằng BCC'B' là hình chữ nhật.
b) Tính theo a thể tích khối lăng trụ ABC.A'B'C'.
c) Tính góc giữa đường thẳng AA' và mặt phẳng (A'B'C').
Lời giải:
a) Kẻ AH B'C' tại H.
Do tam giác AB'C' cân tại A mà AH B'C' nên AH đồng thời là trung tuyến hay H là trung điểm của B'C'.
Do tam giác A'B'C' là tam giác đều mà A'H là trung tuyến nên A'H đồng thời là đường cao hay A'H B'C'.
Vì AH B'C' và A'H B'C' nên B'C' (A'AH), suy ra B'C' A'A.
Do ABB'A' là hình bình hành nên AA' // BB' mà B'C' A'A nên BB' B'C'.
Vì BCC'B' là hình bình hành có BB' B'C' nên BCC'B' là hình chữ nhật.
b) Vì (AB'C') (A'B'C'), (AB'C') (A'B'C') = B'C' mà AH B'C' nên AH (A'B'C').
Suy ra AH A'H hay tam giác AHA' vuông tại H.
Vì tam giác A'B'C' là tam giác đều cạnh a, đường cao A'H nên A'H = , .
Xét tam giác AHA' vuông tại H có: AH = .
Khi đó .
Vậy .
c) Vì AH (A'B'C') nên HA' là hình chiếu của AA' trên mặt phẳng (A'B'C').
Do đó góc giữa đường thẳng AA' và mặt phẳng (A'B'C') bằng góc giữa hai đường thẳng AA' và A'H, mà (AA', A'H) = .
Xét tam giác AA'H vuông tại H có .
Suy ra, .
Vậy góc giữa đường thẳng AA' và mặt phẳng (A'B'C') bằng 60°.
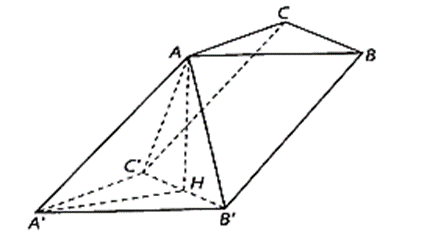
a) Tính theo a thể tích khối hộp chữ nhật.
b) Tính theo a khoảng cách giữa hai đường thẳng BD và CD'.
Lời giải:
a) Vì AA' (ABCD) nên AC là hình chiếu của A'C trên mặt phẳng (ABCD).
Do đó góc giữa đường thẳng A'C và mặt phẳng (ABCD) bằng góc giữa hai đường thẳng A'C và AC, mà (A'C, AC) = .
Vì ABCD là hình chữ nhật nên AB = CD = a; AD = BC = a.
Xét tam giác ABC vuông tại B, có AC = .
Xét tam giác A'AC vuông tại A, có AA' = AC.tan30° = .
Khi đó VABCD.A'B'C'D' = AA' . AB . AD = a.a.a = a3.
b) Có A'D' // BC và A'D' = BC (do cùng song song và bằng AD).
Do đó A'D'CB là hình bình hành, suy ra CD' // BA'. Do đó CD' // (A'DB).
Khi đó d(BD, CD') = d(CD', (A'DB)) = d(D', (A'DB)).
Vì AD' cắt mặt phẳng (A'BD) tại trung điểm của đoạn AD' nên
d(D', (A'DB)) = d(A, (A'DB)) = h.
Áp dụng kết quả bài 7.7 trang 28 SBT Toán tập 2, ta có:
.
Vậy d(BD, CD') .
a) Tính theo a thể tích khối tứ diện AA'MN.
b) Tính côsin góc nhị diện [A, MN, A'].
Lời giải:
a) Ta có d(N,(AMA'))..
Do CC' // AA' nên CC' // (AA'B'B) nên d(N, (AMA')) = d(C, (AA'B'B)).
Kẻ CH AB tại H.
Vì BB' (ABC) nên BB' CH mà CH AB nên CH (AA'B'B).
Do đó d(C, (AA'B'B)) = CH.
Xét tam giác ABC đều cạnh a, CH là đường cao có CH = ,
suy ra d(C, (AA'B'B)) = .
Vì ABB'A' là hình chữ nhật có d(M, AA') = AB = a.
Do đó d(M,AA').AA' = .a.2a = a2.
Vậy .
b) Gọi I là trung điểm của MN.
Vì M, N là trung điểm của BB' và CC' nên CN = C'N, BM = B'M.
Mà AA' = BB' = CC' = 2a nên CN = C'N = BM = B'M = a.
Vì ABC.A'B'C' là hình lăng trụ tam giác đều nên
AB = AC = BC = A'B' = A'C' = B'C' = a.
Xét tam giác CAN vuông tại C, có AN2 = AC2 + CN2 = a2 + a2 = 2a2.
Xét tam giác A'C'N vuông tại C', có A'N2 = A'C'2 + C'N2 = a2 + a2 = 2a2.
Xét tam giác A'B'M vuông tại B', có A'M2 = A'B'2 + B'M2 = a2 + a2 = 2a2.
Xét tam giác ABM vuông tại B, có AM2 = AB2 + BM2 = a2 + a2 = 2a2.
Do đó AN = A'N = A'M = AM.
Xét tam giác A'MN có A'M = A'N nên tam giác A'MN cân tại A' mà A'I là trung tuyến nên A'I đồng thời là đường cao hay A'I MN.
Xét tam giác AMN có AM = AN nên tam giác AMN cân tại A mà AI là trung tuyến nên AI đồng thời là đường cao hay AI MN.
Vì A'I MN và AI MN nên [A, MN, A'] = .
Vì I là trung điểm của MN mà MN = BC = a nên MI = IN = .
Xét tam giác A'MI vuông tại I, có .
Xét tam giác ANI vuông tại I, có .
Áp dụng định lí côsin trong tam giác AA'I, ta có:
.
Vậy côsin góc nhị diện [A, MN, A'] bằng -.
Xem thêm các bài giải SBT Toán lớp 11 Kết nối tri thức hay, chi tiết khác:


 là
là