Giải các phương trình sau: a) 3^(x^2-3x) = 4^4x; b) log3(x^2 – x – 3) = log3(2x – 1) + 1

Bài 32 trang 71 SBT Toán 11 Tập 2: Giải các phương trình sau:

a) $3^{x^2-3x}=4^{4x}$;

b) log₃(x² – x – 3) = log₃(2x – 1) + 1.

Trả lời

a) $3^{x^2-3x}=4^{4x}$$\iff$ x² – 3x = log₃4^4x $\iff$ x² – 3x = 4xlog₃4 $\iff$ x² – 3x − 4xlog₃4 = 0

$\iff$ x(x – 3 − 4log₃4) = 0 $\iff$ x = 0 hoặc x = 3 + 4log₃4.

Vậy tập nghiệm của phương trình là S = {0; 3 + 4log₃4}.

b) Điều kiện .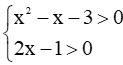

Ta có log₃(x² – x – 3) = log₃(2x – 1) + 1

$\iff$ log₃(x² – x – 3) = log₃(2x – 1) + log₃3

$\iff$ log₃(x² – x – 3) = log₃[3(2x – 1)]

$\iff$ log₃(x² – x – 3) = log₃(6x – 3)

$\iff$ x² – x – 3 = 6x – 3 $\iff$ x² – 7x = 0

$\iff$ x(x – 7) = 0 $\iff$ x = 0 hoặc x = 7.

Đối chiếu với điều kiện thì x = 7 thỏa mãn điều kiện.

Vậy nghiệm của phương trình là x = 7.

Xem thêm các bài giải SBT Toán lớp 11 Kết nối tri thức hay, chi tiết khác: