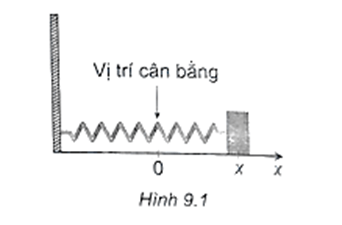
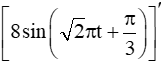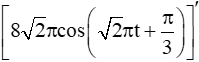Sách bài tập Toán lớp 11 Bài tập cuối chương 9
A. TRẮC NGHIỆM
Bài 9.22 trang 63 SBT Toán 11 Tập 2: Cho f(x) = cos2. Đạo hàm f'(0) bằng
A. 1.
B. −1.
C. 2cos.
D. -2cos.
Lời giải:
Đáp án đúng là: B
Có
.
.
Bài 9.23 trang 63 SBT Toán 11 Tập 2: Cho f(x) = -x3+x2+3x - 1. Đạo hàm f'(x) > 0 khi
A. x < −1.
B. x > 3.
C. −1 < x < 3.
D. x > −1.
Lời giải:
Đáp án đúng là: C
Có = −x2 + 2x + 3.
Để f'(x) > 0 thì −x2 + 2x + 3 > 0 (3 − x)(x + 1) > 0 −1 < x < 3.
Vậy f'(x) > 0 thì −1 < x < 3.
Bài 9.24 trang 63 SBT Toán 11 Tập 2: Đạo hàm của hàm số y = ln|1 – 2x| là
Lời giải:
Đáp án đúng là: C
Có y' = (ln|1 – 2x|)' = . Vậy .
Bài 9.25 trang 63 SBT Toán 11 Tập 2: Đạo hàm của hàm số là
A. .
B. .
C. .
D. .
Lời giải:
Đáp án đúng là: C
Có
.
Vậy .
Bài 9.26 trang 63 SBT Toán 11 Tập 2: Đạo hàm của hàm số là
A. .
B. .
C. .
D. .
Lời giải:
Đáp án đúng là: A
= = .
Vậy .
Bài 9.27 trang 63 SBT Toán 11 Tập 2: Đạo hàm của hàm số y = xsin2x là
A. y' = sin2x + 2xsinx.
B. y' = sin2x + xsin2x.
C. y' = sin2x + 2xcosx.
D. y' = sin2x + xcos2x.
Lời giải:
Đáp án đúng là: B
Có y' = (xsin2x)' = sin2x + x×(sin2x)' = sin2x + 2xsinxcosx = sin2x + xsin2x.
Vậy y' = sin2x + xsin2x.
Bài 9.28 trang 64 SBT Toán 11 Tập 2: Cho hàm số với g(0) = 3, g'(0) = −8. Đạo hàm f'(0) bằng
A. 10.
B. −8.
C. −5.
D. 5.
Lời giải:
Đáp án đúng là: C
.
Có (do g(0) = 3, g'(0) = −8).
Vậy f'(0) = −5.
Bài 9.29 trang 64 SBT Toán 11 Tập 2: Cho f(x) = xsinx và g(x) = . Giá trị là
A. −1.
B. sin1 + cos1.
C. 1.
D. −sin1 − cos1.
Lời giải:
Đáp án đúng là: A
Có f'(x) = (xsinx)' = sinx + xcosx, suy ra f'(1) = sin1 + cos1
,
suy ra g'(1) = = -sin1 - cos1.
Do đó = -1.
Vậy .
Bài 9.30 trang 64 SBT Toán 11 Tập 2: Cho f(x) = x. Tập nghiệm của phương trình f'(x) = 0 là
A. {1}.
B. {−1}.
C. {0; 1}.
D. {−1; 1}.
Lời giải:
Đáp án đúng là: D
Có .
Để f'(x) = 0 thì .
A. (−; 0).
B. (1; +).
C. (−; 0) (1; +).
D. (0; 1).
Lời giải:
Đáp án đúng là: D
Có f'(x) = (2x3 + 3x – 1)' = 6x2 + 3.
g'(x) = [3(x2 + x) + 2]' = 6x + 3.
Để f'(x) < g'(x) thì 6x2 + 3 < 6x + 3 6x2 − 6x < 0 6x(x − 1) < 0 0 < x < 1.
Vậy tập nghiệm của bất phương trình f'(x) < g'(x) là (0; 1).
A. S'(r) là diện tích nửa hình tròn đó.
B. S'(r) là chu vi đường tròn đó.
C. S'(r) là chu vi nửa đường tròn đó.
D. S'(r) là hai lần chu vi đường tròn đó.
Lời giải:
Đáp án đúng là: B
Ta có S(r) = . Do đó S'(r) = ()' = 2r là chu vi của đường tròn đó.
A. y = 6x + 4.
B. y = 6x − 4.
C. y = −2x − 4.
D. y = −2x + 4.
Lời giải:
Đáp án đúng là: A
Có y' = [x(x – 1)2 + x2 + 1]' = (x – 1)2 + 2x(x – 1) + 2x
= x2 – 2x + 1 + 2x2 – 2x + 2x = 3x2 – 2x + 1.
Có y'(−1) = 3×(−1)2 – 2×(−1) + 1 = 6.
Phương trình tiếp tuyến của đồ thị hàm số y = x(x – 1)2 + x2 + 1 tại điểm A(−1; −2) có dạng: y = y'(−1)×(x + 1) – 2 = 6×(x + 1) – 2 = 6x + 6 – 2 = 6x + 4.
Vậy y = 6x + 4 là tiếp tuyến cần tìm.
A. y = 3x − 25.
B. y = −3x + 25.
C. .
D. .
Lời giải:
Đáp án đúng là: C
Hệ số góc của tiếp tuyến của đồ thị hàm số có dạng:
k = y' = = 2x2 – 8x + 5.
Có k = 2x2 – 8x + 5 = 2(x2 – 4x) + 5 = 2(x2 – 4x + 4) – 3 = 2(x – 2)2 – 3 − 3.
Dấu “=” xảy ra khi x – 2 = 0 hay x = 2.
Do đó hệ số góc nhỏ nhất của tiếp tuyến là −3 khi x = 2; y = .
Phương trình tiếp tuyến của đồ thị hàm số là y = -3(x-2)+ = -3x+.
Vậy y = -3x + là tiếp tuyến cần tìm.
A. k = 5.
B. k = 2.
C. k = −2.
D. k = −5.
Lời giải:
Đáp án đúng là: D
Có
.
Hệ số góc của tiếp tuyến của đồ thị hàm số tại điểm có hoành độ x = −1 là:
k = y'(-1) = = -5.
Vậy k = −5 là hệ số góc cần tìm.
A. y = 3x – 5.
B. y = 3x – 7.
C. y = 3x + 5.
D. y = 3x + 7.
Lời giải:
Đáp án đúng là: B
Hệ số góc của tiếp tuyến của đồ thị hàm số có dạng:
k = y' = (−x3 + 6x2 – 9x + 1)' = −3x2 + 12x – 9.
Có k = −3x2 + 12x – 9 = −3(x2 – 4x) – 9 = −3(x2 – 4x + 4) + 3 = −3(x − 2)2 + 3 ≤ 3.
Dấu “=” xảy ra khi x – 2 = 0 hay x = 2.
Do đó hệ số góc lớn nhất của tiếp tuyến của đồ thị hàm số là 3 khi x = 2; y = −1.
Phương trình tiếp tuyến của đồ thị hàm số là y = 3(x – 2) – 1= 3x – 7.
Vậy y = 3x – 7 là tiếp tuyến cần tìm.
Bài 9.37 trang 65 SBT Toán 11 Tập 2: Cho f(x) = (x2 – x)e−x. Giá trị f"(0) là
A. 4.
B. −4.
C. 0.
D. −1.
Lời giải:
Đáp án đúng là: A
Có f'(x) = [(x2 – x)e−x]' = (2x −1)e−x − (x2 – x)e−x = (−x2 + 3x – 1)e−x.
f"(x) = [(−x2 + 3x – 1)e−x]' = (−2x + 3)e−x − (−x2 + 3x – 1)e−x = (x2 – 5x + 4)e−x.
Khi đó f"(0) = (02 – 5×0 + 4)e−0 = 4. Vậy f"(0) = 4.
Bài 9.38 trang 65 SBT Toán 11 Tập 2: Cho hàm số y = excosx. Đẳng thức đúng là
A. y" – 2y' – 2y = 0.
B. y" – 2y' + 2y = 0.
C. y" + 2y' – 2y = 0.
D. y" + 2y' + 2y = 0.
Lời giải:
Đáp án đúng là: B
Có y' = (excosx)' = excosx − exsinx
⇒ y' = y − exsinx ⇒ exsinx = y – y'.
y" = (excosx − exsinx)' = excosx − exsinx – (exsinx + excosx) = −2exsinx = −2(y – y').
Do đó y" = −2(y – y') y" = −2y + 2y' y" – 2y' + 2y = 0.
A. 88,5 m/s.
B. 86,7 m/s.
C. 89,4 m/s.
D. 90 m/s.
Lời giải:
Đáp án đúng là: A
Vận tốc của vật tại thời điểm t là v(t) = h'(t) = (400 – 4,9t2)' = −9,8t.
Khi vật chạm đất tức là h(t) = 0 400 – 4,9t2 = 0 giây.
Giá trị tuyệt đối của vận tốc của vật khi nó chạm đất là 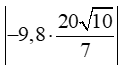
A. 4,5 cm/s2.
B. 5,5 cm/s2.
C. 6,3 cm/s2.
D. 7,1 cm/s2.
Lời giải:
Đáp án đúng là: C
Vận tốc của vật tại thời điểm t là v(t) = s'(t) =
.
Gia tốc của vật tại thời điểm t là a(t) = v'(t) =
.
Tại thời điểm vận tốc bằng 0 tức là
.
Do mà nên
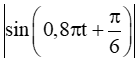
Giá trị tuyệt đối của gia tốc tại thời điểm vận tốc bằng 0 là
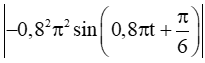
Vậy giá trị tuyệt đối của gia tốc gần 6,3 cm/s2.
A. 140 m/s2.
B. 120 m/s2.
C. 130 m/s2.
D. 100 m/s2.
Lời giải:
Đáp án đúng là: A
Ta có v(t) = s'(t) = 4t3 – 12t2 – 40t + 20.
a(t) = v'(t) = 12t2 – 24t – 40.
Thời điểm mà vận tốc v = 20 m/s tức là 4t3 – 12t2 – 40t + 20 = 20
4t3 – 12t2 – 40t = 0 t = 5 (thỏa mãn) hoặc t = 0 (loại) hoặc t = −2 (loại).
Gia tốc của vật tại thời điểm t = 5 giây là a(5) = 12.52 – 24.5 – 40 = 140 m/s2.
Vậy gia tốc của vật tại thời điểm mà vận tốc v = 20 m/s là 140 m/s2.
B. TỰ LUẬN
Bài 9.42 trang 65 SBT Toán 11 Tập 2: Tính đạo hàm các hàm số sau:
a)
b) y = 2x + log3(1 – 2x);
c) ;
d) y = sin2x + cos23x.
Lời giải:
a) y' =
/
Vậy .
b) y' = [2x + log3(1 – 2x)]' = .
Vậy .
c)
.
Vậy .
d) y' = (sin2x + cos23x)' = cos2x×(2x)' + 2cos3x×(cos3x)'
= 2cos2x – 6cos3xsin3x = 2cos2x – 3sin6x.
Vậy y' = 2cos2x – 3sin6x.
Bài 9.43 trang 65 SBT Toán 11 Tập 2: Cho hàm số f(x) = x + .
a) Tìm tập xác định của hàm số đã cho.
b) Tính đạo hàm f'(x) và tìm tập xác định của f'(x).
Lời giải:
a) Điều kiện 4 – x2 0 −2 ≤ x ≤ 2.
Vậy tập xác định của hàm số là [−2; 2].
b) Có f'(x) = (x+)' = 1 +
.
Điều kiện để f'(x) xác định là 4 – x2 > 0 −2 < x < 2.
Vậy tập xác định của f'(x) là (−2; 2).
c) Có f'(x) = 0 thì
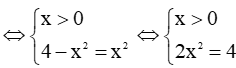
Kết hợp với điều kiện ở câu b, ta có là giá trị cần tìm.
Lời giải:
+) Với x < 0 thì f(x) = x2 – x. Có f'(x) = 2x – 1.
+) Với x > 0 thì f(x) = −x3 + mx. Có f'(x) = −3x2 + m.
Hàm số có đạo hàm tại mọi x ℝ khi và chỉ khi tồn tại f'(0).
Ta đi tính đạo hàm bên trái và đạo hàm bên phải tại điểm x = 0.
Có .
.
Do vậy hàm số có đạo hàm tại mọi x ℝ khi và chỉ khi m = −1.
Vậy m = −1 là giá trị cần tìm.
Lời giải:
Có f'(x) = (x3 + ax2 + 3x + 1)' = 3x2 + 2ax + 3.
Để f'(x) > 0 với mọi x ℝ thì 3x2 + 2ax + 3 > 0 với mọi x ℝ, điều này xảy ra khi và chỉ khi ' = a2 – 9 < 0 −3 < a < 3.
Vậy −3 < a < 3 là giá trị cần tìm.
Lời giải:
Giả sử là điểm thuộc đồ thị (C).
Vì tiếp tuyến tại điểm M song song với đường thẳng có phương trình y = 2x – 1 nên hệ số góc của tiếp tuyến là k = y'(x0) = 2.
Có y'(x0) = .
Vì y'(x0) = 2 nên x0 = 0 hoặc x0 = 2.
+ Với x0 = 0 thì M(0; −1). Khi đó ta có phương trình tiếp tuyến là: y = 2x − 1 trùng với đường thẳng đề cho nên M(0; −1) không thỏa mãn.
+ Với x0 = 2 thì M(2; −1). Khi đó ta có phương trình tiếp tuyến là: y = 2(x – 2) – 1 hay y = 2x – 5.
Vậy M(2; −1) là điểm cần tìm.
Lời giải:
Hoành độ giao điểm của đồ thị hàm số y = (x2 – 1)2 – 3 và đồ thị hàm số y = 10 – x2 là nghiệm của phương trình: (x2 – 1)2 – 3 = 10 – x2
x4 – 2x2 + 1 – 3 = 10 – x2
x4 – x2 – 12 = 0
(x2 + 3)(x2 – 4) = 0
x2 – 4 = 0 (do x2 + 3 > 0 với mọi x)
x = 2 hoặc x = −2.
Với x = 2, ta có tọa độ giao điểm A(2; 6).
Với x = −2, ta có tọa độ giao điểm B(−2; 6).
Có y' = [(x2 – 1)2 – 3]' = 2(x2 – 1)(x2 – 1)' = 4x(x2 – 1).
+) Viết phương trình tiếp tuyến của đồ thị hàm số tại A(2; 6).
Hệ số góc của tiếp tuyến là k = y'(2) = 4×2×(22 – 1) = 24.
Do đó phương trình tiếp tuyến của đồ thị hàm số tại A(2; 6) là:
y = 24(x – 2) + 6 hay y = 24x – 42.
+) Viết phương trình tiếp tuyến của đồ thị hàm số tại B(−2; 6).
Hệ số góc của tiếp tuyến là k = y'(−2) = 4×(−2)×[(−2)2 – 1] = −24.
Do đó phương trình tiếp tuyến của đồ thị hàm số tại B(−2; 6) là:
y = −24(x + 2) + 6 hay y = −24x – 42.
Vậy y = 24x – 42 và y = −24x – 42 là hai tiếp tuyến cần tìm.
Lời giải:
Vận tốc của vật tại thời điểm t là
v(t) = x'(t) =
Gia tốc của vật tại thời điểm t là
a(t) = v'(t) =
.
Vận tốc của vật tại thời điểm t = 5 giây là
m/s.
Gia tốc của vật tại thời điểm t = 5 giây là
m/s2.
Tại thời điểm đó vật đang chuyển động theo hướng từ phải sang trái (hướng tới vách chắn cố định).
Xem thêm các bài giải SBT Toán lớp 11 Kết nối tri thức hay, chi tiết khác:


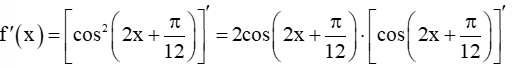
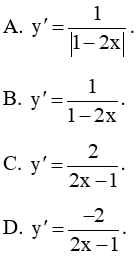
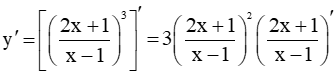
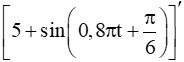
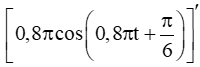
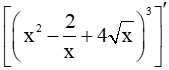
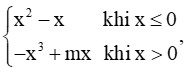 với m là tham số. Tìm m để hàm số có đạo hàm tại mọi x ℝ.
với m là tham số. Tìm m để hàm số có đạo hàm tại mọi x ℝ.