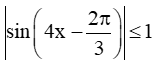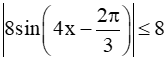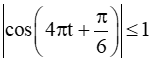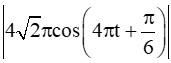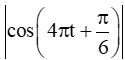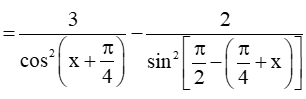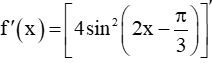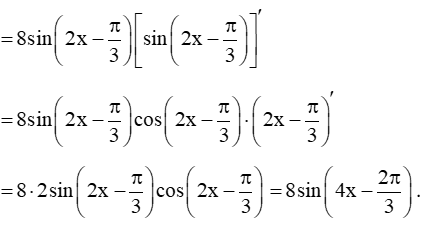Sách bài tập Toán lớp 11 Bài 32: Các quy tắc tính đạo hàm
Bài 9.8 trang 60 SBT Toán 11 Tập 2: Tính đạo hàm của các hàm số sau:
a) y = (x + 1)2(x2 – 1);
b) .
Lời giải:
a) Ta có: y' = ((x + 1)2)'(x2 – 1) + (x + 1)2(x2 – 1)'
= 2(x + 1)(x2 – 1) + 2x(x + 1)2
= 2x3 – 2x + 2x2 – 2 + 2x3 + 4x2 + 2x = 4x3 + 6x2 – 2.
Vậy y' = 4x3 + 6x2 – 2.
b)
.
Bài 9.9 trang 60 SBT Toán 11 Tập 2: Tính đạo hàm của các hàm số sau:
a) ;
b) .
Lời giải:
a)
.
Vậy .
b)
.
Bài 9.10 trang 60 SBT Toán 11 Tập 2: Cho hàm số và . Tính f'(0) – g'(1).
Lời giải:
Có
.
Khi đó .
Có .
Khi đó .
Do đó f'(0) – g'(1) = . Vậy f'(0) – g'(1) = 0.
Bài 9.11 trang 60 SBT Toán 11 Tập 2: Tính đạo hàm của hàm số .
Lời giải:
Có
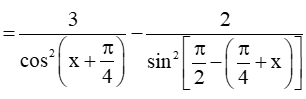
Bài 9.12 trang 60 SBT Toán 11 Tập 2: Cho hàm số . Tính đạo hàm f'(x) và chứng tỏ f'(x) = 0 với mọi x ℝ.
Lời giải:
Có
= -sin2x + 2cossin2x = -sin2x + sin2x = 0.
Vậy f'(x) = 0 với mọi x ℝ.
Bài 9.13 trang 60 SBT Toán 11 Tập 2: Cho hàm số f(x) = 4sin2. Chứng minh rằng |f'(x)| ≤ 8 với mọi x ℝ. Tìm x để f'(x) = 8.
Lời giải:
+ Có 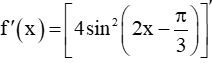
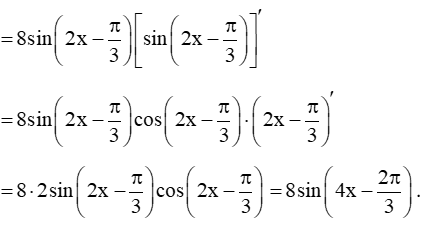
Vì 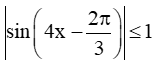 với mọi x ℝ nên
với mọi x ℝ nên 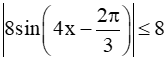 với mọi x ℝ .
với mọi x ℝ .
Vậy |f'(x)| ≤ 8 với mọi x ℝ.
+ Có f'(x) = 8 8sin=8
(k ℤ)
(k ℤ)
(k ℤ).
Vậy f'(x) = 8 khi với k ℤ.
Bài 9.14 trang 60 SBT Toán 11 Tập 2: Biết y là hàm số của x thỏa mãn phương trình xy = 1 + lny. Tính y'(0).
Lời giải:
Đạo hàm hai vế của phương trình đã cho, ta có
(xy)' = (1 + lny)' y + xy' =
y = - xy' y = y'.
y = y' y' = .
Tại x = 0 thay vào phương trình xy = 1 + lny ta được lny = −1 y = e−1.
Do đó .
Vậy .
Bài 9.15 trang 60 SBT Toán 11 Tập 2: Một vật được phóng thẳng đứng lên trên từ mặt đất với vận tốc ban đầu là v0 (m/s) (bỏ qua sức cản của không khí) thì độ cao h của vật (tính bằng mét) sau t giây được cho bởi công thức (g là gia tốc trọng trường). Tính vận tốc khi vật chạm đất.
Lời giải:
Vận tốc của vật tại thời điểm t là v(t) = h'(t) = = vo - gt.
Tại thời điểm vật chạm đất thì h = 0 (t > 0) tức là vot - gt2 = 0
.
Vận tốc khi vật chạm đất là (m/s).
Vậy vận tốc khi vật chạm đất là −v0 m/s.
Bài 9.16 trang 60 SBT Toán 11 Tập 2: Chuyển động của một hạt trên một dây rung được cho bởi công thức , trong đó s tính bằng centimét và t tính bằng giây. Tính vận tốc của hạt sau t giây. Vận tốc cực đại của hạt là bao nhiêu? (Làm tròn kết quả đến chữ số thập phân thứ nhất).
Lời giải:
Vận tốc của hạt sau t giây là v(t) = s'(t) =
.
Vì 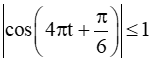 nên
nên 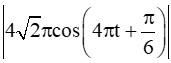 4 hay |v(t)|4.
4 hay |v(t)|4.
Do đó vận tốc cực đại của hạt là 417,8 m/s đạt được khi 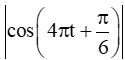 = 1
= 1
, với k ℕ*.
Vậy vận tốc cực đại của hạt khoảng 17,8 m/s khi ,với k ℕ*.
Xem thêm các bài giải SBT Toán lớp 11 Kết nối tri thức hay, chi tiết khác:
Câu hỏi liên quan
Có y' = (3tan(x + pi/4) - 2cot(pi/4 - x))
Xem thêm
Có f'(x) = (cos^2 x + cos^2*(2pi/3 + x) + cos^2*(2pi/3 - x))'
Xem thêm
Vận tốc của hạt sau t giây là v(t) = s'(t) = (10+căn 2 sin(4pit + pi/6))'
Xem thêm
Đạo hàm hai vế của phương trình đã cho, ta có
Xem thêm
+ Có f'(x) = [4sin^2(2x-pi/3)]'
Xem thêm
Vận tốc của vật tại thời điểm t là v(t) = h'(t) = (v0t - 1/2gt^2) = vo - gt.
Xem thêm
Có f'(x) = (x / căn (4-x^2))' = x' * căn (4-x^2) - x * (căn (4-x^2))' / 4-x^2
Xem thêm
a) Ta có: y' = ((x + 1)^2)'(x^2 – 1) + (x + 1)^2(x^2 – 1)'
Xem thêm
Xem tất cả hỏi đáp với chuyên mục: Các quy tắc tính đạo hàm (SBT KNTT)
Được cập nhật 21/11/2023
316 lượt xem