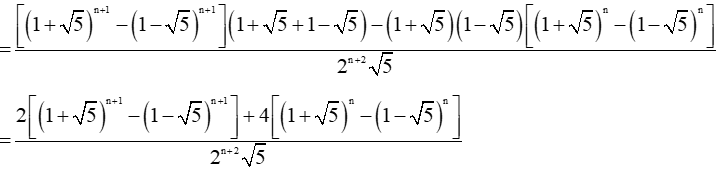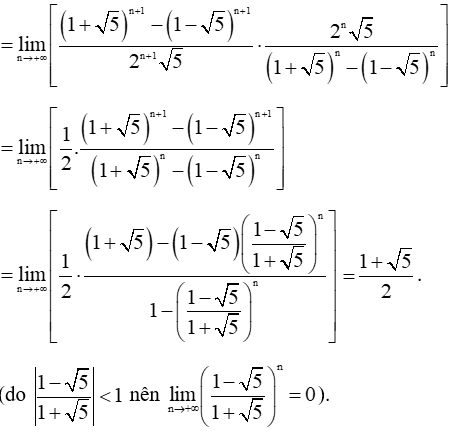Giả sử un là số hạng thứ n của dãy số (un) và un = (1 + căn 5)^n - (1 - căn 5)^n / 2^n * căn 5

Bài 29 trang 70 SBT Toán 11 Tập 2: Giả sử u_n là số hạng thứ n của dãy số (u_n) và $u_n=\frac{{\left(1+\sqrt{5}\right)}^n-{\left(1-\sqrt{5}\right)}^n}{2^n\sqrt{5}}$.

a) Chứng tỏ rằng u₁ = 1, u₂ = 1 và u_{n + 2} = u_{n + 1} + u_n với mọi n $\in$ ℕ^*. Từ đó suy ra (u_n) là dãy số Fibonacci.

b) Viết 11 số hạng đầu tiên của dãy Fibonacci và 10 tỉ số $\frac{u_{n+1}}{u_n}$ đầu tiên.

Tính $\underset{n\to +\infty }{\lim }\frac{u_{n+1}}{u_n}$.

Trả lời

a) Ta có a^{n + 2} – b^{n + 2} = a^{n + 1}.a − b^{n + 1}.b

= a^{n + 1}.a + a^{n + 1}.b − b^{n + 1}.b − b^{n + 1}.a − a^{n + 1}.b + b^{n + 1}.a

= a^{n + 1}.(a + b) − b^{n + 1}.(a + b) – ab(aⁿ − bⁿ)

= (a^{n + 1} − b^{n + 1}).(a + b) – ab(aⁿ − bⁿ) (*)

Có $u_1=\frac{{\left(1+\sqrt{5}\right)}^1-{\left(1-\sqrt{5}\right)}^1}{2^1\sqrt{5}}$$=\frac{2\sqrt{5}}{2\sqrt{5}}=1$.

$u_2=\frac{{\left(1+\sqrt{5}\right)}^2-{\left(1-\sqrt{5}\right)}^2}{2^2\sqrt{5}}$$=\frac{4\sqrt{5}}{4\sqrt{5}}=1$.

Áp dụng (*), ta có:

$u_{n+2}=\frac{{\left(1+\sqrt{5}\right)}^{n+2}-{\left(1-\sqrt{5}\right)}^{n+2}}{2^{n+2}\sqrt{5}}$

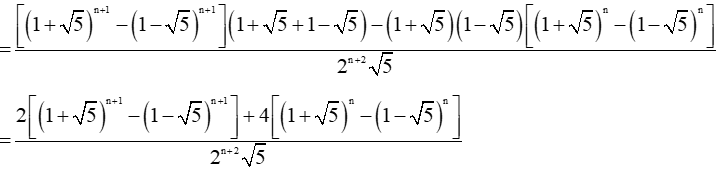
$=\frac{{\left(1+\sqrt{5}\right)}^{n+1}-{\left(1-\sqrt{5}\right)}^{n+1}}{2^{n+1}\sqrt{5}}+\frac{{\left(1+\sqrt{5}\right)}^n-{\left(1-\sqrt{5}\right)}^n}{2^n\sqrt{5}}$ = u_n+1 + u_n.

Vậy u_{n + 2} = u_n+1 + u_n. Do đó (u_n) là dãy Fibonacci.

b) Ta có bảng sau

Ta có $\underset{n\to +\infty }{\lim }\frac{u_{n+1}}{u_n}$$=\underset{n\to +\infty }{\lim }\frac{\frac{{\left(1+\sqrt{5}\right)}^{n+1}-{\left(1-\sqrt{5}\right)}^{n+1}}{2^{n+1}\sqrt{5}}}{\frac{{\left(1+\sqrt{5}\right)}^n-{\left(1-\sqrt{5}\right)}^n}{2^n\sqrt{5}}}$

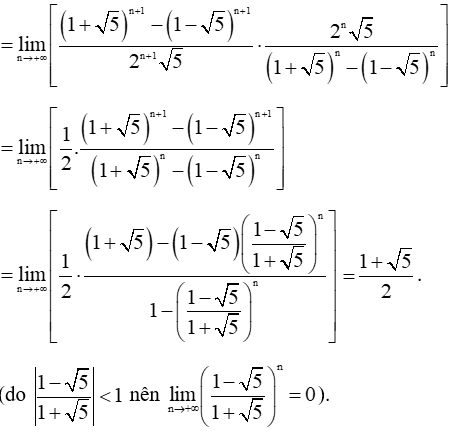
Xem thêm các bài giải SBT Toán lớp 11 Kết nối tri thức hay, chi tiết khác: