Cho hình chóp S.ABCD có mặt phẳng (SAB) vuông góc với mặt đáy (ABCD), tam giác SAB đều

Bài 20 trang 69 SBT Toán 11 Tập 2: Cho hình chóp S.ABCD có mặt phẳng (SAB) vuông góc với mặt đáy (ABCD), tam giác SAB đều, đáy ABCD là hình vuông cạnh bằng a. Gọi H là trung điểm của cạnh AB. Khoảng cách từ điểm H đến mặt phẳng (SAC) bằng

A. $\frac{a\sqrt{30}}{5}$ .

B. $\frac{a\sqrt{30}}{10}$ .

C. $\frac{a\sqrt{6}}{10}$ .

D. $\frac{a\sqrt{6}}{5}$ .

Trả lời

Đáp án đúng là: E. $\frac{a\sqrt{21}}{14}$ .

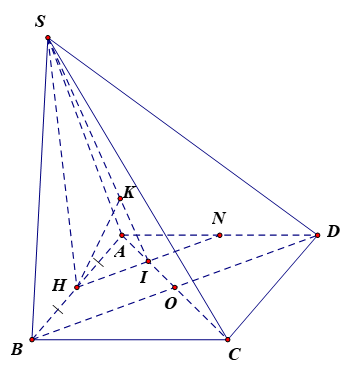
Vì tam giác SAB đều, H là trung điểm của AB nên SH là đường cao hay SH $\perp$ AB.

Do (SAB) $\perp$ (ABCD); (SAB) $\cap$ (ABCD) = AB mà SH $\perp$ AB nên SH $\perp$ (ABCD), suy ra SH $\perp$ AC.

Gọi N là trung điểm của AD.

Xét tam giác ABD có H là trung điểm của AB, N là trung điểm của AD nên HN là đường trung bình của tam giác ABD, suy ra HN // BD.

Do ABCD là hình vuông nên AC $\perp$ BD mà HN // BD nên HN $\perp$ AC.

Vì HN $\perp$ AC và SH $\perp$ AC nên AC $\perp$ (SHN), suy ra (SAC) $\perp$ (SHN).

Gọi AC $\cap$ HN = I, kẻ HK $\perp$ SI tại K.

Vì (SAC) $\perp$ (SHN), (SAC) $\cap$ (SHN) = SI mà HK $\perp$ SI nên HK $\perp$ (SAC).

Do đó d(H, (SAC)) = HK.

Gọi O là giao điểm của AC và BD.

Vì ABCD là hình vuông nên O là trung điểm của BD.

Xét tam giác ABD vuông tại A, có $BD=\sqrt{A{B}^2+A{D}^2}=\sqrt{a^2+a^2}=a\sqrt{2}$ .

Vì O là trung điểm của BD nên BO = $\frac{BD}{2}$= $\frac{a\sqrt{2}}{2}$.

Xét tam giác ABO có H là trung điểm của AB, HI // BO (do HN //BD) nên I là trung điểm của AO.

Vì I là trung điểm của AO, H là trung điểm của AB nên HI là đường trung bình của tam giác ABO, suy ra $HI=\frac{BO}{2}=\frac{a\sqrt{2}}{4}$ .

Vì tam giác SAB là tam giác đều cạnh a, SH là đường cao nên $SH=\frac{a\sqrt{3}}{2}$ .

Vì SH $\perp$ (ABCD) nên SH $\perp$ HI hay tam giác SHI vuông tại H.

Xét tam giác SHI vuông tại H, HK là đường cao, có:

$\frac{1}{H{K}^2}=\frac{1}{S{H}^2}+\frac{1}{H{I}^2}$$=\frac{4}{3a^2}+\frac{16}{2a^2}$$=\frac{28}{3a^2}$$\Rightarrow HK=\frac{a\sqrt{21}}{14}$.

Vậy d(H, (SAC)) = $\frac{a\sqrt{21}}{14}$ .

Xem thêm các bài giải SBT Toán lớp 11 Kết nối tri thức hay, chi tiết khác: