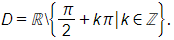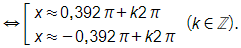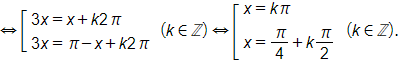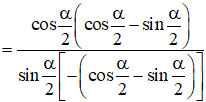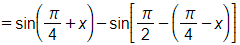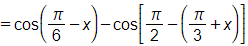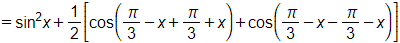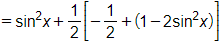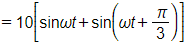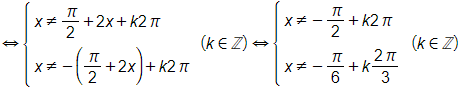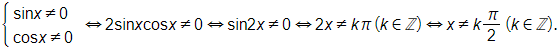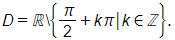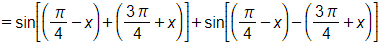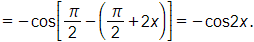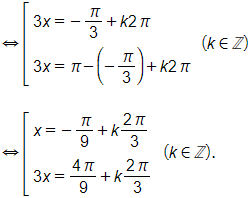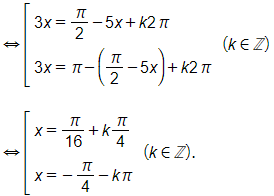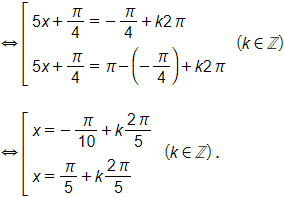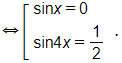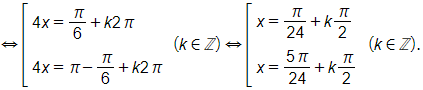Giải SBT Toán lớp 11 Bài tập cuối chương 1 trang 25
A. TRẮC NGHIỆM
Bài 1.31 trang 25 SBT Toán 11 Tập 1: Đổi số đo góc α = 105° sang rađian ta được
A. .
B. .
C. .
D. .
Lời giải:
Đáp án đúng là: C
Ta có α = 105° = rad.
A. Có số nguyên k để .
B. .
C. .
D. .
Lời giải:
Đáp án đúng là: A
Vì có vô số góc lượng giác tia đầu Ou, tia cuối Ov nên ta loại trừ đáp án B, C, D (do chưa thể xác định được khoảng cụ thể của góc α.
Mà là góc tù nên .
Vậy tồn tại số nguyên k để .
Bài 1.33 trang 25 SBT Toán 11 Tập 1: Giá trị bằng
A. .
B. .
C. .
D. .
Lời giải:
Đáp án đúng là: C
Ta có .
Bài 1.34 trang 25 SBT Toán 11 Tập 1: Cho . Mệnh đề nào sau đây đúng?
A. sin α < 0; cos α > 0.
B. sin α > 0; cos α > 0.
C. sin α < 0; cos α < 0.
D. sin α > 0; cos α < 0.
Lời giải:
Đáp án đúng là: D
Vì nên α thuộc góc phần tư thứ II, do đó sin α > 0, cos α < 0.
Bài 1.35 trang 25 SBT Toán 11 Tập 1: Trong các đẳng thức sau, đẳng thức nào sai?
A. .
B. .
C. .
D. .
Lời giải:
Đáp án đúng là: D
Theo mối quan hệ giữa giá trị lượng giác của hai góc phụ nhau, ta có:
; nên đáp án A và C đúng.
Ta có 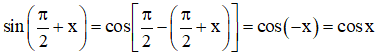
Lại có 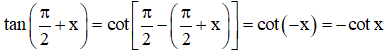
Bài 1.36 trang 26 SBT Toán 11 Tập 1: Trong các đẳng thức sau, đẳng thức nào đúng?
A. sin(180° – a) = – cos a.
B. sin(180° – a) = – sin a.
C. sin(180° – a) = sin a.
D. sin(180° – a) = cos a.
Lời giải:
Đáp án đúng là: C
Theo mối quan hệ giữa giá trị lượng giác của hai góc bù nhau, ta có: sin(180° – a) = sin a.
Bài 1.37 trang 26 SBT Toán 11 Tập 1: Biết sin x = . Giá trị của cos2 x bằng
A. .
B. .
C. .
D. .
Lời giải:
Đáp án đúng là: D
Ta có sin2 x + cos2 x = 1, suy ra cos2 x = 1 – sin2 x = .
Bài 1.38 trang 26 SBT Toán 11 Tập 1: Biết cot x = . Giá trị của biểu thức bằng
A. .
B. .
C. 13.
D. .
Lời giải:
Đáp án đúng là: C
Vì cot x = nên sin x ≠ 0, ta chia cả tử và mẫu của biểu thức cho sin x, ta được:
.
Bài 1.39 trang 26 SBT Toán 11 Tập 1: Trong các đẳng thức sau, đẳng thức nào sai?
A. .
B. .
C. .
D. .
Lời giải:
Đáp án đúng là: B
Công thức biến đổi tổng thành tích:
.
.
.
.
Vậy đáp án B sai.
Bài 1.40 trang 26 SBT Toán 11 Tập 1: Trong các đẳng thức sau, đẳng thức nào sai?
A. sin 2a = 2sin a cos a.
B. cos 2a = cos2 a – sin2 a.
C. cos 2a = 1 – 2sin2 a.
D. tan 2a = .
Lời giải:
Đáp án đúng là: D
Công thức nhân đôi:
sin 2a = 2sin a cos a.
cos 2a = cos2 a – sin2 a = 1 – 2sin2 a.
tan 2a = .
Vậy đáp án D sai.
Bài 1.41 trang 26 SBT Toán 11 Tập 1: Tập xác định của hàm số là
Lời giải:
Đáp án đúng là: D
Biểu thức xác định khi 1 – cos x ≥ 0.
Vì – 1 ≤ cos x ≤ 1 nên 1 – cos x ≥ 0 với mọi x ∈ ℝ.
Vậy tập xác định của hàm số là D = ℝ.
Bài 1.42 trang 26 SBT Toán 11 Tập 1: Khẳng định nào sau đây đúng?
A. Hàm số y = cos x nghịch biến trên khoảng (– π; 0) và đồng biến khoảng (0; π).
B. Hàm số y = cos x đồng biến trên các khoảng (– π; 0) và (0; π).
C. Hàm số y = cos x nghịch biến trên các khoảng (– π; 0) và (0; π).
D. Hàm số y = cos x đồng biến trên khoảng (– π; 0) và nghịch biến trên khoảng (0; π).
Lời giải:
Đáp án đúng là: D
Hàm số y = cos x đồng biến trên mỗi khoảng (– π + k2π; k2π) và nghịch biến trên mỗi khoảng (k2π; π + k2π), k ∈ ℤ.
Do đó, hàm số y = cos x đồng biến trên khoảng (– π; 0) và nghịch biến trên khoảng (0; π).
Bài 1.43 trang 27 SBT Toán 11 Tập 1: Khẳng định nào sau đây sai?
A. Tập xác định của hàm số y = tan x là
B. Hàm số y = tan x đồng biến trên các khoảng với mọi k ∈ ℤ.
C. Tập giá trị của hàm số y = tan x là .
D. Hàm số y = tan x là hàm số tuần hoàn với chu kì π.
Lời giải:
Đáp án đúng là: C
Theo lí thuyết, ta có các đáp án A, B, D đúng.
Lại có tập giá trị của hàm số y = tan x là ℝ nên đáp án C sai.
Bài 1.44 trang 27 SBT Toán 11 Tập 1: Hàm số nào dưới đây có đồ thị nhận trục tung làm trục đối xứng?
A. y = cos x.
B. y = sin3 x .
C. y = sin x.
D. y = tan x.
Lời giải:
Đáp án đúng là: A
Hàm số y = cos x là hàm số chẵn nên đồ thị của nó nhận trục tung làm trục đối xứng.
Bài 1.45 trang 27 SBT Toán 11 Tập 1: Mệnh đề nào sau đây sai?
A. Hàm số y = sin x tuần hoàn với chu kì 2π.
B. Hàm số y = cos x tuần hoàn với chu kì 2π.
C. Hàm số y = tan x tuần hoàn với chu kì 2π.
D. Hàm số y = cot x tuần hoàn với chu kì π.
Lời giải:
Đáp án đúng là: C
Hàm số y = tan x tuần hoàn với chu kì π nên đáp án C sai.
Bài 1.46 trang 27 SBT Toán 11 Tập 1: Mệnh đề nào sau đây sai?
A. Hàm số y = sin x cos 2x là hàm số tuần hoàn.
B. Hàm số y = sin x cos 2x là hàm số lẻ.
C. Hàm số y = x sin x là hàm số tuần hoàn.
D. Hàm số y = x sin x là hàm số chẵn.
Lời giải:
Đáp án đúng là: C
Xét từng đáp án:
+) Hàm số y = sin x cos 2x có tập xác định D = ℝ.
- Ta có ∀ x ∈ D thì x + 2π ∈ D và x – 2π ∈ D, hơn nữa
f(x + 2π) = sin(x + 2π) cos(2x + 2π) = sin x cos 2x = f(x).
Vậy hàm số y = sin x cos 2x là hàm số tuần hoàn nên đáp án A đúng.
- Ta có ∀ x ∈ D thì – x ∈ D và f(– x) = sin(– x) . cos(– 2x) = – sin x . cos 2x = – f(x).
Do đó hàm số y = sin x cos 2x là hàm số lẻ nên đáp án B đúng.
+) Hàm số y = x sin x có tập xác định D = ℝ.
Ta có ∀ x ∈ D thì – x ∈ D và f(– x) = (– x) . sin(– x) = x sin x = f(x).
Do đó hàm số y = x sin x là hàm số chẵn nên đáp án D đúng.
Vậy đáp án C sai.
Bài 1.47 trang 27 SBT Toán 11 Tập 1: Mệnh đề nào dưới đây đúng?
A. cos x = – 1 ⇔ x = π + k2π (k ∈ ℤ).
B. sin x = 0 ⇔ x = k2π (k ∈ ℤ).
C. tan x = 0 ⇔ x = k2π (k ∈ ℤ).
D. cos x = 0 ⇔ x = + k2π (k ∈ ℤ).
Lời giải:
Đáp án đúng là: A
Xét từng đáp án:
+) cos x = – 1 ⇔ x = π + k2π (k ∈ ℤ) nên đáp án A đúng.
+) sin x = 0 ⇔ x = kπ (k ∈ ℤ) nên đáp án B sai, từ đó suy ra đáp án C sai.
+) cos x = 0 ⇔ x = + kπ (k ∈ ℤ) nên đáp án D sai.
Bài 1.48 trang 27 SBT Toán 11 Tập 1: Số nghiệm của phương trình trên đoạn ![Số nghiệm của phương trình 2cosx = căn bậc hai 3 trên đoạn [0;5π/2] là](https://vietjack.com/sbt-toan-11-kn/images/bai-1-48-trang-27-sbt-toan-lop-11-tap-1.PNG)
A. 1.
B. 4.
C. 3.
D. 2.
Lời giải:
Đáp án đúng là: C
Ta có .
Vì ![Số nghiệm của phương trình 2cosx = căn bậc hai 3 trên đoạn [0;5π/2] là](https://vietjack.com/sbt-toan-11-kn/images/bai-1-48-trang-27-sbt-toan-lop-11-tap-1-1.PNG)
+ Với thì , mà k ∈ ℤ, từ đó suy ra k ∈ {0; 1}.
+ Với thì , mà k ∈ ℤ, từ đó suy ra k = 1.
Vậy phương trình có 3 nghiệm trên đoạn ![Số nghiệm của phương trình 2cosx = căn bậc hai 3 trên đoạn [0;5π/2] là](https://vietjack.com/sbt-toan-11-kn/images/bai-1-48-trang-27-sbt-toan-lop-11-tap-1.PNG)
A. S = 2π.
B. S = 0.
C. S = 4π.
D. S = 3π.
Lời giải:
Đáp án đúng là: A
Ta có 3cos x – 1 = 0
Mà x ∈ (0; 2π) nên x ≈ 0,392π hoặc x ≈ – 0,392π + 2π.
Vậy tổng các nghiệm cần tìm là S = 0,392π + (– 0,392π + 2π) = 2π.
Lời giải:
Đáp án đúng là: A
Giá trị của hai hàm số y = sin3x và y = sin x bằng nhau khi và chỉ khi sin 3x = sin x
B. TỰ LUẬN
a) ; b) ; c) – 1 380°.
Lời giải:
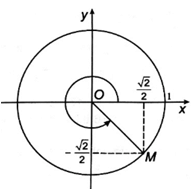
a) Ta có . Góc được biểu diễn bởi điểm trên đường tròn lượng giác (hình dưới).
Vậy và .
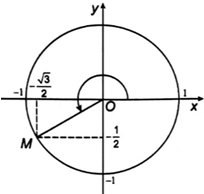
b) Ta có . Góс được biểu diễn bởi điểm > trên đường tròn lượng giác (hình dưới).
Vậy ; và .
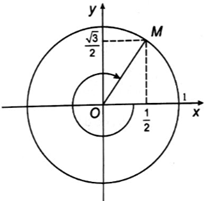
c) Ta có – 1 380° = − 4 . 360° + 60°. Góc –1 380° được biểu diễn bởi điểm trên đường tròn lượng giác (hình dưới).
Vậy sin(– 1 380°) = ; cos(– 1 380°) = ; tan(– 1 380°) = và cot(– 1 380°) = .
Lời giải:
+) Trong 15 phút thì mũi kim phút vạch nên một cung tròn có độ dài bằng độ dài đường tròn, do đó độ dài của cung này bằng
.
+) Trong 15 phút thì mũi kim giờ vạch nên một cung tròn có độ dài bằng đường tròn, do đó độ dài của cung này bằng
.
Lời giải:
Góc ở tâm chắn cung kinh tuyến nối huyện Quản Bạ tỉnh Hà Giang và huyện Cái Nước tỉnh Cà Mau có số đo bằng 23° – 9° = 14°.
Vậy độ dài cung kinh tuyến đó bằng .
Bài 1.54 trang 28 SBT Toán 11 Tập 1: Cho cos α = , sin α > 0; sin β = , . Hãy tính cos 2α, sin 2α, cos 2β, sin 2β, cos (α + β), sin (α – β).
Lời giải:
Ta có cos 2α = 2 cos2 α – 1 = .
Ta có sin2 α = 1 – cos2 a = = .
Lại do sin α > 0 nên sin α = .
Suy ra sin 2α = 2 sin α cos α = .
Ta có cos 2β = 1 – 2 sin2 β = = .
Ta có cos2 β = 1 – sin2 β = = .
Lại do nên cos β < 0, do đó .
Suy ra sin 2β = 2 sin β cos β = .
Ta có
cos(α + β) = cos α cos β – sin α sin β = .
sin(α – β) = sin α cos β – cos α sin β = .
Bài 1.55 trang 28 SBT Toán 11 Tập 1: Rút gọn các biểu thức sau
a) ;
b) ;
c) ;
d) .
Lời giải:
a)
.
b)
.
c)
.
d)
.
Bài 1.56 trang 28 SBT Toán 11 Tập 1: Chứng minh các biểu thức sau không phụ thuộc vào x:
a) ;
b) ;
c) ;
d) .
Lời giải:
a) Cách 1:
.
Vậy biểu thức A không phụ thuộc vào biến x.
Cách 2:
.
Vậy biểu thức A không phụ thuộc vào biến x.
b)
.
Vậy biểu thức B không phụ thuộc vào biến x.
c)
.
Vậy biểu thức C không phụ thuộc vào biến x.
d)
.
Vậy biểu thức D không phụ thuộc vào biến x.
Bài 1.57 trang 29 SBT Toán 11 Tập 1: Hai sóng âm có phương trình lần lượt là
f1(t) = C sin ωt và f2(t) = C sin(ωt + α).
Hai sóng này giao thoa với nhau tạo ra một âm kết hợp có phương trình
f(t) = f1(t) + f2(t) = C sin ωt + C sin(ωt + α).
a) Sử dụng công thức cộng chỉ ra rằng hàm f(t) có thể viết được dưới dạng f(t) = A sin ωt + B cos ωt, ở đó A, B là hai hằng số phụ thuộc vào α.
b) Khi C = 10 và , hãy tìm biên độ và pha ban đầu của sóng âm kết hợp, tức là tìm hai hằng số k và φ sao cho f(t) = k sin(ωt + φ).
Lời giải:
a) Ta có f(t) = f1(t) + f2(t)
= C sin ωt + C sin(ωt + α)
= C sin ωt + C(sin ωt cos α + cos ωt sin α)
= C sin ωt + C sin ωt cos α + C cos ωt sin α
= C(1 + cos α) sin ωt + C sin α cos ωt.
Vậy f(t) = C(1 + cos α) sin ωt + C sin α cos ωt với A = C(1 + cos α) và B = C sin α.
b) Khi C = 10 và ta có
.
Vậy biên độ và pha ban đầu của sóng âm kết hợp lần lượt là và .
Bài 1.58 trang 29 SBT Toán 11 Tập 1: Tìm tập xác định của các hàm số sau:
a) ;
b) ;
c) ;
d) y = tan x + cot x.
Lời giải:
a) Biểu thức có nghĩa khi x – 1 ≠ 0 hay x ≠ 1.
Vậy tập xác định của hàm số là 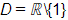
b) Biểu thức có nghĩa khi cos x – cos 3x ≠ 0 hay cos x ≠ cos 3x
⇔ 3x ≠ ± x + k2π (k ∈ ℤ) ⇔ x ≠ k(k ∈ ℤ). .
Vậy tập xác định của hàm số là 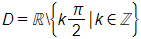
c) Biểu thức có nghĩa khi cos x + sin 2x ≠ 0 ⇔ cos x ≠ – sin 2x
⇔ cos x ≠ sin (– 2x)
Vậy tập xác định của hàm số là 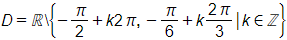
d) Biểu thức tan x + cot x có nghĩa khi
Vậy tập xác định của hàm số là 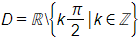
Bài 1.59 trang 29 SBT Toán 11 Tập 1: Tìm giá trị lớn nhất và giá trị nhỏ nhất của p
a) y = sin x – cos x;
b) y = sin x + sin;
c) y = sin4 x + cos4 x;
d) y = cos 2x + 2cos x – 1.
Lời giải:
a) Ta có y = sin x – cos x = .
Vì nên , với mọi .
Vậy giá trị lớn nhất của hàm số là , đạt được khi
>.
Giá trị nhỏ nhất của hàm số là , đạt được khi
.
b) Ta có y = sin x + sin
.
Ta có .
Vậy giá trị lớn nhất của hàm số là 1, đạt được khi và giá trị nhỏ nhất của hàm số là – 1, đạt được khi .
c) Ta có y = sin4 x + cos4 x = (sin2 x + cos2 x)2 – 2sin2 x cos2 x
= 1 – 2 (sin x cos x)2 = =
= = = .
Vì – 1 ≤ cos 4x ≤ 1 nên , do đó
hay .
Vậy giá trị lớn nhất của hàm số là 1, đạt được khi cos 4x = 1 ⇔ 4x = k2π (k ∈ ℤ)
.
Giá trị nhỏ nhất của hàm số là , đạt được khi cos 4x = – 1 ⇔ 4x = π + k2π (k ∈ ℤ)
.
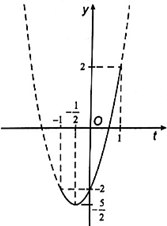
d) Ta có y = cos 2x + 2cos x − 1
= (2cos2 x – 1) + 2cos x – 1
= 2cos2 x + 2cos x – 2
= 2t2 + 2t – 2 với t = cos x ∈ [– 1; 1].
Xét hàm số y = 2t2 + 2t – 2 trên đoạn [– 1; 1]. Hàm số này có đồ thị như trong hình vẽ dưới đây.
Từ đồ thị ở hình trên ta suy ra được giá trị lớn nhất của hàm số đã cho là 2, đạt được khi cos x = 1 ⇔ x = k2π (k ∈ ℤ) và giá trị nhỏ nhất của hàm số là , đạt được khi .
Bài 1.60 trang 29 SBT Toán 11 Tập 1: Xét tính chẵn lẻ của các hàm số sau:
a) y = sin3 x – cot x;
b) ;
c) y = sin 2x + cos x;
d) .
Lời giải:
a) Tập xác định của hàm số y = sin3 x – cot x là D = ℝ \ {kπ | k ∈ ℤ}.
Nếu kí hiệu f(x) = sin3 x + cot x thì với mọi x ∈ D ta có: – x ∈ D và
f(– x) = sin3 (–x) – cot(– x) = – sin3 x + cot x = – (sin3 x – cot x) = – f(x).
Vậy hàm số đã cho là hàm số lẻ.
b) Tập xác định của hàm số là
Nếu kí hiệu thì với mọi x ∈ D ta có: – x ∈ D và
Vậy hàm số đã cho là hàm số chẵn.
c) Tập xác định của hàm số y = sin 2x + cos x là D = ℝ.
Nếu kí hiệu f(x) = sin 2x + cos x thì với mọi x ∈ D ta có: – x ∈ D và
f(– x) = sin [2(– x)] + cos (– x) = – sin 2x + cos x ≠ ± f(x).
Vậy hàm số đã cho là hàm số không chẵn cũng không lẻ.
d) Tập xác định của hàm số là D = ℝ.
Ta có
Nếu kí hiệu thì với mọi x ∈ D ta có: – x ∈ D và f(– x) = – cos (– 2x) = – cos 2x = f(x).
Vậy hàm số đã cho là hàm số chẵn.
Bài 1.61 trang 29 SBT Toán 11 Tập 1: Xét tính tuần hoàn của các hàm số sau:
a) y = sin + cos 3x;
b) y = cos 5x + tan.
Lời giải:
a) Hàm số y = sin tuần hoàn với chu kì T1 = , hàm số y = cos 3x tuần hoàn với chu kì T2 = . Ta có .
Ta chỉ ra rằng hàm số f(x) = = sin + cos 3x tuần hoàn như sau:
.
Vậy hàm số đã cho là hàm số tuần hoàn với chu kì T = 4π.
b) Hàm số y = cos 5x tuần hoàn với chu kì T1 = null, hàm số y = tan hoàn với chu kì .
Ta có .
Ta có thể chỉ ra hàm số f(x) = cos5x + tan tuần hoàn như sau
.
Vậy hàm số đã cho là hàm số tuần hoàn với chu kì T = 6π.
Bài 1.62 trang 29 SBT Toán 11 Tập 1: Giải các phương trình sau:
a) ;
b) ;
c) sin 3x – cos 5x = 0;
d) tan 3x tan x = 1.
Lời giải:
a) Ta có
b) Ta có
⇔ + 10° = – 30° + k180° (k ∈ ℤ)
⇔ x = – 120° + k540° (k ∈ ℤ).
c) Ta có sin 3x – cos 5x = 0
⇔ sin 3x = cos 5x
d) Điều kiện cos 3x ≠ 0 và cos x ≠ 0 ⇔ cos3x ≠ 0 .
Ta có tan 3x tan x = 1
⇔ tan 3x = cot x
.
Ta thấy thoả mãn điều kiện.
Vậy nghiệm của phương trình là .
Bài 1.63 trang 30 SBT Toán 11 Tập 1: Giải các phương trình sau:
a) sin 5x + cos 5x = – 1;
b) cos 3x – cos 5x = sin x;
c) 2 cos2 x + cos 2x = 2;
d) sin4 x + cos4 x = sin2 2x.
Lời giải:
a) Ta có sin 5x + cos 5x = – 1
b) Ta có cos 3x – cos 5x = sin x
+ Với sin x = 0 ta được x = kπ (k ∈ ℤ).
+ Với
c) Ta có 2 cos2 x + cos 2x = 2
⇔ (2 cos2 x – 1) + cos 2x = 1
⇔ cos 2x + cos 2x = 1
⇔ 2cos 2x = 1
⇔ cos 2x =
⇔ cos 2x =
⇔ 2x =
.
d) Ta có sin4 x + cos4 x = sin2 2x
(do sin2 2x + cos2 2x = 1)
.
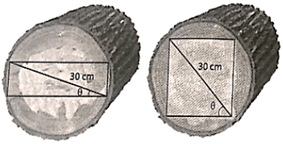
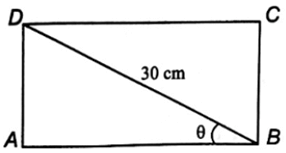
a) Chứng minh rằng diện tích mặt cắt của thanh xà gồ được tính bởi công thức
S(θ) = 450 sin 2θ (cm2),
ở đó góc θ được chỉ ra trong hình vẽ dưới đây.
b) Tìm góc θ để diện tích mặt cắt của thanh xà gồ là lớn nhất.
Lời giải:
a) Mặt cắt của thanh xà gồ (hình dưới) là hình chữ nhật có hai kích thước là
AB = 30cos θ và BC = 30sin θ.
Vậy diện tích mặt cắt là S = AB ∙ BC = 30cos θ ∙ 30sin θ = 450sin 2θ.
b) Vì – 1 ≤ sin 2θ ≤ 1 nên ta có S = 450sin 2θ ≤ 450.
Vậy diện tích mặt cắt của thanh xà gồ lớn nhất khi sin 2θ = 1 hay góc θ = 45°.
ở đó P(t) là huyết áp tính theo đơn vị mmHg (milimét thuỷ ngân) và thời gian t tính theo giây.
a) Trong khoảng từ 0 đến 1 giây, hãy xác định số lần huyết áp là 100 mmHg.
b) Trong khoảng từ 0 đến 1 giây, hãy xác định số lần huyết áp là 120 mmHg
Lời giải:
a) Huyết áp là 100 mmHg khi
.
Xét 0 < t < 1 . Suy ra k ∈ {1; 2} vì k ∈ ℤ.
Vậy trong khoảng từ 0 đến 1 giây, có 2 lần huyết áp là 100 mmHg.
b) Huyết áp là 120 mmHg khi
.
Xét 0 < t < 1 . Suy ra k = 0 vì k ∈ ℤ.
Vậy trong khoảng từ 0 đến 1 giây, có 1 lần huyết áp là 120 mmHg.
a) Huyết áp là 100 mmHg khi
.
Xét 0 < t < 1 . Suy ra k ∈ {1; 2} vì k ∈ ℤ.
Vậy trong khoảng từ 0 đến 1 giây, có 2 lần huyết áp là 100 mmHg.
b) Huyết áp là 120 mmHg khi
.
Xét 0 < t < 1 . Suy ra k = 0 vì k ∈ ℤ.
Vậy trong khoảng từ 0 đến 1 giây, có 1 lần huyết áp là 120 mmHg.
Xem thêm các bài giải SBT Toán lớp 11 Kết nối tri thức hay, chi tiết khác: