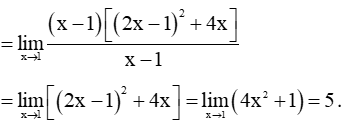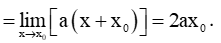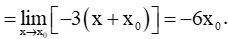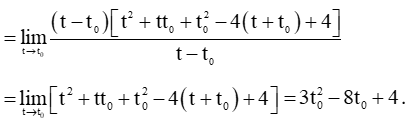Giải SBT Toán 11 (Kết nối tri thức) Bài 31: Định nghĩa và ý nghĩa của đạo hàm

Sách bài tập Toán lớp 11 Bài 31: Định nghĩa và ý nghĩa của đạo hàm

Bài 9.1 trang 57 SBT Toán 11 Tập 2: Tính (bằng định nghĩa) đạo hàm của hàm số y = 2x² + 3x – 1 tại điểm x₀ = 1.

Lời giải:

Tại điểm x₀ = 1 ta có y₀ = 2×1² + 3×1 – 1 = 4.

Với x ≠ 1, ta có $\frac{y-4}{x-1}=\frac{2x^2+3x-1-4}{x-1}$$=\frac{2x^2+3x-5}{x-1}$

$=\frac{\left(2x+5\right)\left(x-1\right)}{x-1}=2x+5$ .

Do đó y'(1) = $\underset{x\to 1}{\lim }\frac{y-4}{x-1}=$$\underset{x\to 1}{\lim }$(2x+5) = 7. Vậy y'(1) = 7.

Bài 9.2 trang 57 SBT Toán 11 Tập 2: Cho hàm số f(x) = x(2x – 1)². Tính f'(0) và f'(1).

Lời giải:

+ Có f'(0) = $\underset{x\to 0}{\lim }\frac{f\left(x\right)-f\left(0\right)}{x-0}$$=\underset{x\to 0}{\lim }\frac{x{\left(2x-1\right)}^2}{x}$$=\underset{x\to 0}{\lim }$(2x-1)² = 1.

Vậy f'(0) = 1.

+ Có f'(1) = $\underset{x\to 1}{\lim }\frac{f\left(x\right)-f\left(1\right)}{x-1}$$=\underset{x\to 1}{\lim }\frac{x{\left(2x-1\right)}^2-1}{x-1}$

$=\underset{x\to 1}{\lim }\frac{\left(x-1\right){\left(2x-1\right)}^2+{\left(2x-1\right)}^2-1}{x-1}$

$=\underset{x\to 1}{\lim }\frac{\left(x-1\right){\left(2x-1\right)}^2+\left(2x-1-1\right)\left(2x-1+1\right)}{x-1}$

$=\underset{x\to 1}{\lim }\frac{\left(x-1\right){\left(2x-1\right)}^2+4x\left(x-1\right)}{x-1}$

Vậy f'(1) = 5.

Bài 9.3 trang 57 SBT Toán 11 Tập 2: Cho hàm số f(x) = 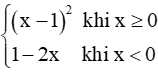 . Tính f'(0).

Lời giải:

Ta có f(0) = (0 – 1)² = 1.

Ta có $\underset{x\to 0^{+}}{\lim }\frac{f\left(x\right)-f\left(0\right)}{x-0}$$=\underset{x\to 0^{+}}{\lim }\frac{{\left(x-1\right)}^2-1}{x}$$=\underset{x\to 0^{+}}{\lim }\frac{x^2-2x}{x}$$=\underset{x\to 0^{+}}{\lim }$(x-2) = -2 ;

$\underset{x\to 0^{-}}{\lim }\frac{f\left(x\right)-f\left(0\right)}{x-0}$$=\underset{x\to 0^{-}}{\lim }\frac{1-2x-1}{x}$$=\underset{x\to 0^{-}}{\lim }\frac{-2x}{x}=-2$.

Suy ra $\underset{x\to 0}{\lim }\frac{f\left(x\right)-f\left(0\right)}{x-0}=\underset{x\to 0^{+}}{\lim }\frac{f\left(x\right)-f\left(0\right)}{x-0}=\underset{x\to 0^{-}}{\lim }\frac{f\left(x\right)-f\left(0\right)}{x-0}=-2$ .

Vậy f'(0) = −2.

Bài 9.4 trang 57 SBT Toán 11 Tập 2: Tính đạo hàm của hàm số:

a) y = ax² (a là hằng số) tại điểm x₀ bất kì.

b) $y=\frac{1}{x-1}$ tại điểm x₀ bất kì, x₀ ≠ 1.

Lời giải:

a) Đặt y = f(x) = ax².

Ta có y'(x₀) = $\underset{x\to x_0}{\lim }\frac{f\left(x\right)-f\left(x_0\right)}{x-x_0}$$=\underset{x\to x_0}{\lim }\frac{a{x}^2-a{x}_0^2}{x-x_0}$

$=\underset{x\to x_0}{\lim }\frac{a\left(x^2-x_0^2\right)}{x-x_0}$$=\underset{x\to x_0}{\lim }\frac{a\left(x-x_0\right)\left(x+x_0\right)}{x-x_0}$

Vậy y'(x₀) = 2ax₀.

b) Đặt y = f(x) = $\frac{1}{x-1}$.

Ta có y'(x₀) = $\underset{x\to x_0}{\lim }\frac{f\left(x\right)-f\left(x_0\right)}{x-x_0}$$=\underset{x\to x_0}{\lim }\frac{\frac{1}{x-1}-\frac{1}{x_0-1}}{x-x_0}$

$=\underset{x\to x_0}{\lim }\frac{\frac{x_0-1-\left(x-1\right)}{\left(x-1\right)\left(x_0-1\right)}}{x-x_0}$$=\underset{x\to x_0}{\lim }\frac{\frac{\left(x_0-x\right)}{\left(x-1\right)\left(x_0-1\right)}}{x-x_0}$

$=\underset{x\to x_0}{\lim }\frac{-1}{\left(x-1\right)\left(x_0-1\right)}$$=\frac{-1}{{\left(x_0-1\right)}^2}$.

Vậy $y^{\text{'}}\left(x_0\right)=\frac{-1}{{\left(x_0-1\right)}^2}$ , x₀ ≠ 1.

Bài 9.5 trang 57 SBT Toán 11 Tập 2: Tìm tọa độ điểm M trên đồ thị hàm số y = x³ + 1, biết hệ số góc của tiếp tuyến của đồ thị hàm số tại M bằng 3.

Lời giải:

Giả sử M(a; a³ + 1) là điểm thuộc đồ thị hàm số y = x³ + 1.

Đặt y = f(x) = x³ + 1. Có y'(a) = $\underset{x\to a}{\lim }\frac{f\left(x\right)-f\left(a\right)}{x-a}$

$=\underset{x\to a}{\lim }\frac{x^3+1-\left(a^3+1\right)}{x-a}$$=\underset{x\to a}{\lim }\frac{x^3-a^3}{x-a}$

$=\underset{x\to a}{\lim }\frac{\left(x-a\right)\left(x^2+ax+a^2\right)}{x-a}$

$=\underset{x\to a}{\lim }\left(x^2+ax+a^2\right)=3a^2$.

Theo đề bài, ta có y'(a) = 3 nên 3a² = 3 $\iff$ a = 1 hoặc a = −1.

Với a = 1 thì M(1; 2);

Với a = −1 thì M(−1; 0).

Vậy M(1; 2) và M(−1; 0) là tọa độ điểm cần tìm.

Bài 9.6 trang 57 SBT Toán 11 Tập 2: Viết phương trình tiếp tuyến của đồ thị hàm số y = −3x², biết tiếp tuyến đó song song với đường thẳng có phương trình y = 6x + 5.

Lời giải:

Đặt y = f(x) = −3x². Với x₀ bất kì, ta có:

y'(x₀) = $\underset{x\to x_0}{\lim }\frac{f\left(x\right)-f\left(x_0\right)}{x-x_0}$$=\underset{x\to x_0}{\lim }\frac{-3x^2+3x_0^2}{x-x_0}$

$=\underset{x\to x_0}{\lim }\frac{-3\left(x^2-x_0^2\right)}{x-x_0}$$=\underset{x\to x_0}{\lim }\frac{-3\left(x-x_0\right)\left(x+x_0\right)}{x-x_0}$

Khi đó hệ số góc của tiếp tuyến có dạng k = y'(x₀) = −6x₀ (x = x₀ là hoành độ tiếp điểm).

Do tiếp tuyến song song với đường thẳng có phương trình y = 6x + 5 nên hệ số góc của tiếp tuyến là k = 6. Do đó −6x₀ = 6 $\iff$ x₀ = −1.

Với x₀ = −1 thì y(−1) = −3.

Khi đó, ta có phương trình tiếp tuyến là: y + 3 = 6(x + 1) hay y = 6x + 3.

Vậy y = 6x + 3 là phương trình tiếp tuyến cần tìm.

Bài 9.7 trang 57 SBT Toán 11 Tập 2: Vị trí của một vật chuyển động thẳng được cho bởi phương trình s = t³ – 4t² + 4t, trong đó t tính bằng giây và s tính bằng mét. Tính vận tốc của vật tại các thời điểm t = 3 giây và t = 5 giây.

Lời giải:

Ta có vận tốc của vật tại thời điểm t₀ bất kì là

v(t₀) = s'(t₀) = $\underset{t\to t_0}{\lim }\frac{s\left(t\right)-s\left(t_0\right)}{t-t_0}$

$=\underset{t\to t_0}{\lim }\frac{t^3-4t^2+4t-\left(t_0^3-4t_0^2+4t_0\right)}{t-t_0}$

$=\underset{t\to t_0}{\lim }\frac{\left(t^3-t_0^3\right)-4\left(t^2-t_0^2\right)+4\left(t-t_0\right)}{t-t_0}$

$=\underset{t\to t_0}{\lim }\frac{\left(t-t_0\right)\left(t^2+t{t}_0+t_0^2\right)-4\left(t-t_0\right)\left(t+t_0\right)+4\left(t-t_0\right)}{t-t_0}$

Vận tốc của vật tại thời điểm t = 3 giây là v(3) = 3×3² − 8×3 + 4 = 7 m/s.

Vận tốc của vật tại thời điểm t = 5 giây là v(5) = 3×5² − 8×5 + 4 = 39 m/s.

Xem thêm các bài giải SBT Toán lớp 11 Kết nối tri thức hay, chi tiết khác: