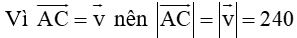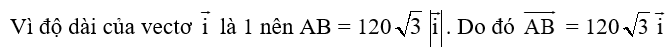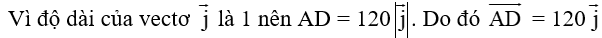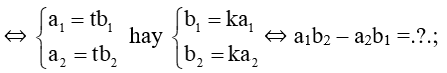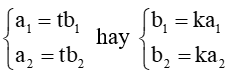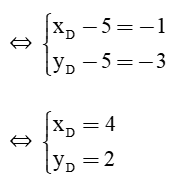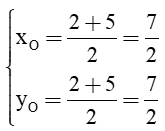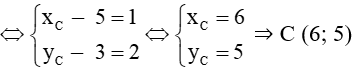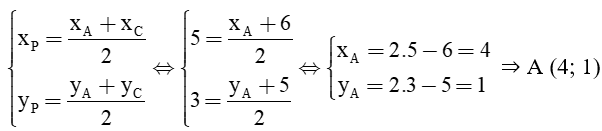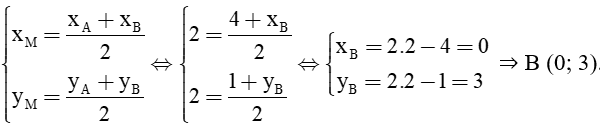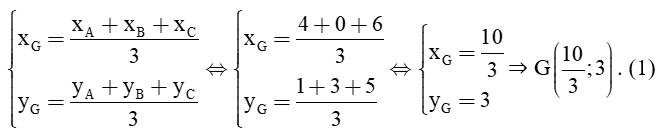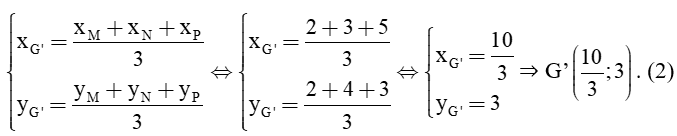Giải Toán 10 Bài 1: Toạ độ của vectơ
Lời giải:
Đặt hệ trục tọa độ Oxy như hình vẽ:
Vị trí của quân mã A là tọa độ của điểm A trên hệ trục tọa độ Oxy. Tọa độ điểm A(2,5; 2,5).
Vị trí quân mã B là tọa độ của điểm B trên hệ trục tọa độ Oxy. Tọa độ điểm B(4,5; 3,5).
Vị trí quân mã C là tọa độ của điểm C trên hệ trục tọa độ Oxy. Tọa độ điểm C(5,5; 2,5).
Vị trí quân mã D là tọa độ của điểm D trên hệ trục tọa độ Oxy. Tọa độ điểm D(1,5; 7,5).
1. Toạ độ của vectơ đối với một hệ trục toạ độ
Lời giải:
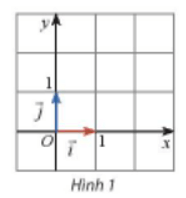
Vectơ →i có phương trùng với trục Ox, chiều trùng với chiều dương của Ox và độ lớn là 1.
Vectơ →j có phương trùng với trục Oy, chiều trùng với chiều dương của Oy và độ lớn là 1.
Lời giải:
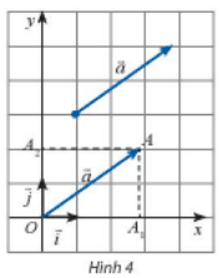
Xét bình hành OA1AA2, có:
→OA=→OA1+→OA2(quy tắc hình bình hành)
⇒ →OA=x→i+y→j
Mà →OA=→a nên →a=x→i+y→j.
Vậy →a=x→i+y→j.
Lời giải:
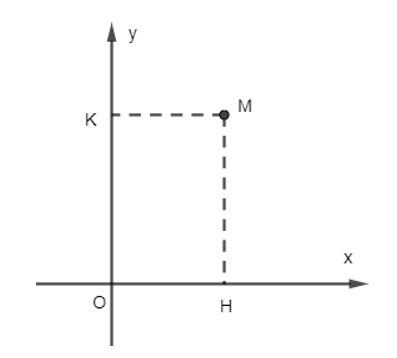
Giả sử M(x; y).
Kẻ MH ⊥ Ox, và MK ⊥ Oy.
⇒→OH=x→i,→OK=y→j
Xét tứ giác OHMK có ^MHO=^MKO=^HOK=90°
Suy ra OHMK là hình chữ nhật hay cũng chính là hình bình hành, khi đó ta có:
Do đó = (x; y).
Vậy tọa độ vectơ (x; y).
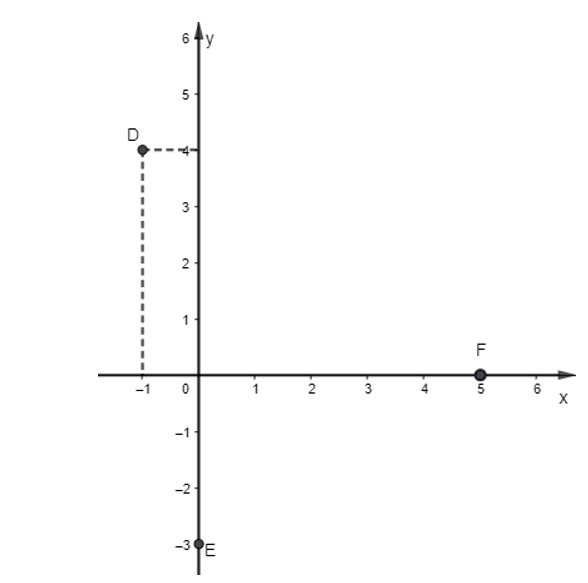
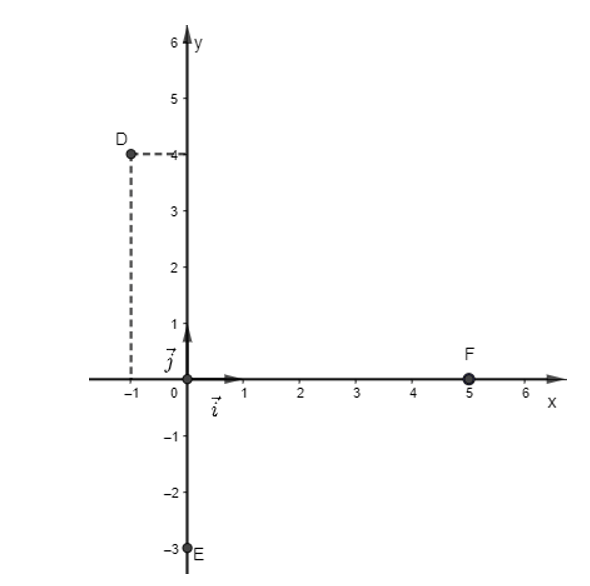
a) Vẽ các điểm D, E, F trên mặt phẳng Oxy.
b) Tìm tọa độ của các vectơ .
c) Vẽ và tìm tọa độ hai vectơ đơn vị và lần lượt trên hai trục tọa độ Ox và Oy.
Lời giải:
a) Các điểm D, E, F được biểu diễn trên mặt phẳng Oxy như sau:
b) Tọa độ vectơ được gọi là tọa độ của điểm D nên .
Tọa độ vectơ được gọi là tọa độ của điểm E nên .
Tọa độ vectơ được gọi là tọa độ của điểm F nên .
c) Hai vectơ đơn vị và được biểu diễn lần lượt trên hai trục tọa độ Ox và Oy là:
Tọa độ của vectơ và .
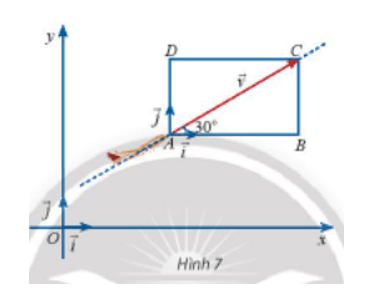
a) Tính độ dài mỗi cạnh của hình chữ nhật ABCD.
b) Biểu diễn vectơ vận tốc theo hai vectơ và .
c) Tìm tọa độ vectơ của .
Lời giải:
a)
Xét tam giác ABC vuông tại B, có:
AB = cos30°.AC = 120
BC = sin30°.AC = 120
Vậy AB = DC = 120 và AD = BC = 120.
b) Vectơ cùng phương và cùng chiều với vectơ .
Vectơ cùng phương và cùng chiều với vectơ .
Xét hình chữ nhật ABCD, có:
(quy tắc hình bình hành)
⇒
⇒ .
c) Vì nên tọa độ của vectơ .
2. Biểu thức toạ độ của các phép toán vectơ
a) Biểu diễn từng vectơ , ; k theo hai vectơ , .
b) Tìm . theo tọa độ của hai vectơ , .
Lời giải:
a) Ta có:
;
;
.
b) Ta có:
. =
= a1b1 + a2b2 (vì và ).
Thực hành 2 trang 41 Toán lớp 10 Tập 2: Cho hai vectơ = (-6; 1) và = (0; 2).
a) Tìm tọa độ của các vectơ , , , .
b) Tính các tích vô hướng , .
Lời giải:
a) Ta có:
= (-6 + 0; 1 + 2) = (-6; 3);
= (-6 – 0; 1 – 2) = (-6; -1);
= 10(-6; 1) = (-60; 10);
= -4(0; 2) = (0; -8).
b) Tính các tích vô hướng:
= (-6).0 + 1.2 = 2;
= -60.0 + 10.(-8) = -80.
Lời giải:
Ta có: = (10 + 3,5; -8 + 0) = (13,5; -8).
Vậy tọa độ của vectơ tổng hai vận tốc và là (13,5; -8).
3. Áp dụng của toạ độ vectơ
Lời giải:
Ta có tọa độ của vectơ chính là tọa độ của điểm A nên ta có (xA; yA).
Tọa độ của vectơ chính là tọa độ của điểm B nên ta có (xB; yB).
Khi đó: = (xB – xA; yB – yA).
Thực hành 3 trang 42 Toán lớp 10 Tập 2: Cho E((9; 9), F(8; -7), G(0; -6). Tìm tọa độ của các vectơ .
Lời giải:
Ta có tọa độ của các vectơ như sau:
= (9 – 8; 9 – (-7)) = (1; 16);
= (0 – 8; - 6 – (-7)) = (-8; 1);
= (0 – 9; -6 – 9) = (-9; -15).
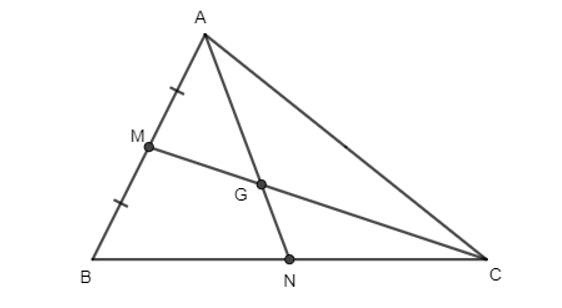
a) Biểu thị vectơ theo hai vectơ và .
b) Biểu thị vectơ theo hai vectơ , và .
c) Từ các kết quả trên, tìm tọa độ điểm M và G theo tọa độ của các điểm A, B, C.
Lời giải:
a)
Vì M là trung điểm của AB nên ta có:
⇔ .
b) Ta có
Mà
Do đó
Hay
c) Tọa độ của là tọa độ của điểm M nên = (xM; yM);
Tọa độ của là tọa độ của điểm A nên = (xA; yA);
Tọa độ của là tọa độ của điểm B nên = (xB; yB);
Vì nên ta có .
Vậy .
Tọa độ của là tọa độ của điểm G nên = (xG; yG);
Tọa độ của là tọa độ của điểm A nên = (xA; yA);
Tọa độ của là tọa độ của điểm B nên = (xB; yB);
Tọa độ của là tọa độ của điểm C nên = (xC; yC);
Vì nên ta có .
Vậy .
a) Tìm tọa độ trung điểm M của cạnh QS.
b) Tìm tọa độ trọng tâm G của tam giác QRS.
Lời giải:
a) Gọi tọa độ của điểm M là M(xM; yM). Vì M là trung điểm của QS nên ta có:
và .
Vậy M(6; 3).
b) Gọi tọa độ của điểm G là G(xG; yG). Vì G là trọng tâm của QRS nên ta có:
và .
Vậy G.
a) ⇔ ⇔ a1.b1 + a2.b2 = .?.;
b) và cùng phương
c)
d) = (xB – xA; yB – yA) ⇒ AB = ;
e) cos (, khác ).
Lời giải:
a) ⇔ ⇔ a1.b1 + a2.b2 = 0
b) và cùng phương
⇔
⇔ a1b2 – a2b1 = 0;
c) Ta có:
Ta điền .
d) = (xB – xA; yB – yA)
⇒ AB = ;
e) cos (, khác ).
a) Tìm tọa độ điểm H là chân đường cao của tam giác DEF kẻ từ D.
b) Giải tam giác DEF.
Lời giải:
a) Gọi H(xH; yH).
Ta có: , ,
Vì H thuộc EF nên và cùng phương.
Khi đó:
⇒
Vì DH EF nên
⇔ (-yH + 6).(-4) + (yH – 2).4 = 0
⇔ 4yH – 24 + 4yH – 8 = 0
⇔ 8yH = 32
⇔ yH = 4
⇒ xH = - 4 + 8 = 4
Vậy H(4; 4).
b) Ta có:
⇒ DE = ;
⇒ EF = ;
⇒ DF = ;
Ta lại có EF2 = = 32 và DE2 + DF2 = 42 + 42 = 32
Suy ra EF2 = DE2 + DF2
Theo định lí Py – ta – go đảo ta có: ∆DEF vuông tại D
Mà DE = DF nên tam giác DEF vuông cân tại D.
Suy ra .
Vậy DE = DF = 4, EF = 4, .
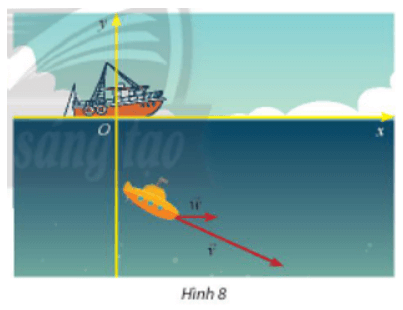
a) Tính số đo của .
b) Cho biết một đơn vị trên hệ trục tọa độ tương ứng với 1km. Tính khoảng cách từ con tàu đến mỗi hòn đảo.
Lời giải:
a) Ta có: và
Khi đó 60.42 + 10.(-43) = 2 090
Ta lại có:
cos
= cos
⇒ ≈ 55,24°.
Vậy ≈ 55,24°.
b) Ta có:
⇒ AB = ≈ 60,83.
⇒ AC = ≈ 60,11.
Vì một đơn vị trên hệ trục tọa độ tương ứng với 1km nên khoảng cách từ vị trí của con tàu tới đảo B là 60,83 km và tới đảo C là 60,11 km.
Bài tập
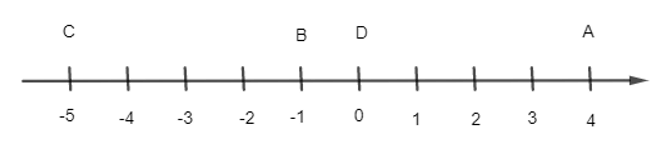
a) Vẽ trục và biểu diễn các điểm đã cho trên trục đó.
b) Hai vectơ và cùng hướng hay ngược hướng?
Lời giải:
a) Các điểm A, B, C, D được biểu diễn trên trục số là:
b) Quan sát hình vẽ ta thấy:
Hai vectơ và ngược hướng nhau.
Bài 2 trang 45 Toán lớp 10 Tập 2: Chứng minh rằng:
a) = (4; -6) và = (-2; 3) là hai vectơ ngược hướng.
b) = (-2; 3) và = (-8; 12) là hai vectơ cùng hướng.
c) = (0; 4) và = (0; -4) là hai vectơ đối nhau.
Lời giải:
a) Ta có: . Do đó = -2
Vì – 2 < 0 nên ngược hướng với .
b) Ta có: . Do đó =
Vì nên cùng hướng với .
c) Ta có = -. Do đó và là hai vectơ đối nhau.
Bài 3 trang 45 Toán lớp 10 Tập 2: Tìm tọa độ của các vectơ sau:
Lời giải:
a) Ta có: nên tọa độ của vectơ (2; 7).
Vậy (2; 7).
b) Ta có nên tọa độ của (-1; 3).
Vậy (-1; 3).
c) Ta có nên tọa độ của (4; 0).
Vậy (4; 0).
d) Ta có nên tọa độ của (0; -9).
Vậy (0; -9).
a) Thuộc trục hoành;
b) Thuộc trục tung;
c) Thuộc đường phân giác của góc phần tư thứ nhất.
Lời giải:
a) Các điểm thuộc trục hoành sẽ có tung độ bằng 0. Do đó chỉ có điểm B thỏa mãn. Vậy điểm B thuộc trục hoành.
b) Các điểm thuộc trục tung sẽ có hoành độ bằng 0. Do đó chỉ có điểm C thỏa mãn. Vậy điểm C thuộc trục tung.
c) Các điểm thuộc phân giác của góc phần tư thứ nhất sẽ có khoảng cách đến hai trục tọa độ bằng nhau hay chính là điểm đó có hoành độ bằng tung độ. Do đó có điểm D thỏa mãn. Vậy D là điểm thuộc đường phân giác của góc phần tư thứ nhất.
Bài 5 trang 45 Toán lớp 10 Tập 2: Cho điểm M(x0; y0). Tìm tọa độ:
a) Điểm H là hình chiếu vuông góc của điểm M trên trục Ox;
b) Điểm M’ đối xứng với điểm M qua trục Ox;
c) Điểm K là hình chiếu vuông góc của điểm M trên trục Oy;
d) Điểm M’’ là điểm đối xứng với điểm M qua trục Oy;
e) Điểm C đối xứng với M qua gốc tọa độ.
Lời giải:
a) Vì điểm H là hình chiếu vuông góc của điểm M trên trục Ox nên tọa độ của điểm H là (x0; 0).
b) Vì điểm M’ đối xứng với điểm M qua trục Ox nên hoành độ điểm M và M’ bằng nhau, còn tung độ điểm M bằng và tung độ điểm M’ đối nhau.
Do đó tọa độ điểm M’ là (x0; -y0).
Vậy M’(x0; -y0).
c) Vì điểm K là hình chiếu vuông góc của điểm M trên trục Oy nên hoành độ của điểm K bằng 0 và tung điểm K là tung độ của điểm M. Do đó tọa độ điểm K là (0; y0).
Vậy tọa độ điểm K(0; y0).
d) Vì điểm M’’ là điểm đối xứng với điểm M qua trục Oy nên tung độ của điểm M’’ bằng tung độ của điểm M, còn hoành độ điểm M’’ và hoành độ điểm M là hai số đối của nhau. Do đó tọa độ điểm M’’ là (-x0; y0).
Vậy M’’(x0; - y0).
e) Vì điểm C đối xứng với M qua gốc tọa độ nên hoành độ và tung độ của điểm C là số đối của lần lượt hoành độ và tung độ của điểm M. Do đó tọa độ điểm C là (-x0; -y0).
Vậy C(-x0; -y0).
Bài 6 trang 45 Toán lớp 10 Tập 2: Cho ba điểm A(2; 2), B(3; 5), C(5; 5).
a) Tìm tọa độ điểm D sao cho ABCD là một hình bình hành.
b) Tìm tọa độ giao điểm hai đường chéo của một hình bình hành ABCD.
Lời giải:
a) Gọi D(xD; yD)
Ta có: = (-1; -3);
Để ABCD là một hình bình hành thì
Vậy D(4; 2).
b) Gọi O là giao điểm hai đường chéo của hình bình hành ABCD. Suy ra O là trung điểm của AC.
Khi đó tọa độ điểm O là:
⇒ O.
Vậy O.
c) Ta có: (-1; -3) ⇒ BA = .
(-3; -3) ⇒ CA = .
(2; 0) ⇒ BC = .
Áp dụng định lí cosin, ta có:
cosA =
⇒ ≈ 26,56°
⇒ sinA =
Áp dụng định lí sin, ta có:
⇒ = 45°.
Ta lại có:
Vậy BA = , CA , BC = 2, ≈ 26,56°, , = 45°.
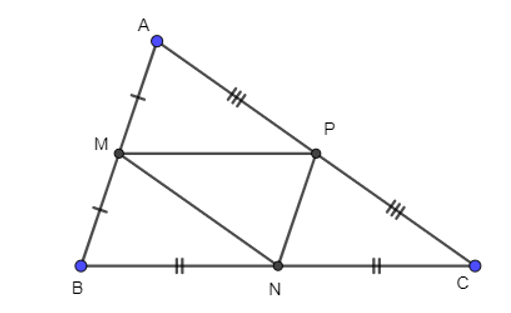
a) Tìm tọa độ các đỉnh của tam giác ABC.
b) Chứng minh rằng trọng tâm của tam giác ABC và MNP trùng nhau.
c) Giải tam giác ABC.
Lời giải:
a) Gọi A(xA; yA), B(xB; yB), C(xC; yC).
Xét tam giác ABC, có:
M là trung điểm của AB
N là trung điểm của AC
Suy ra MN là đường trung bình của tam giác ABC
⇒ MN//AC hay MN //CP và MN // PA và MN = AP = PC = AC
Ta có: , (xC – 5; yC – 3)
Mà
Vì P là trung điểm của AC nên ta có tọa độ P thỏa mãn hệ phương trình:
Vì M là trung điểm của AB nên ta có tọa độ M thỏa mãn hệ phương trình:
Vậy tọa độ các đỉnh của tam giác ABC lần lượt là: A(4; 1), B(0; 3) và C(6; 5).
b) Xét tam giác ABC, có A(4; 1), B(0; 3) và C(6; 5):
Gọi G là trọng tâm của tam giác ABC. Khi đó tọa độ trọng tâm của tam giác ABC là:
Xét tam giác MNP, có M(2; 2), N(3; 4), P(5; 3).
Gọi G là trọng tâm của tam giác MNP. Khi đó tọa độ trọng tâm của tam giác MNP là:
Từ (1) và (2) suy ra G và G’ trùng nhau.
Vậy tam giác ABC và tam giác MNP trùng trọng tâm.
c) Ta có: ⇒ AB = = ;
⇒ AC = = ;
⇒ BC = .
Xét tam giác ABC:
Áp dụng hệ quả của định lí cosin, ta có:
cosA =
⇒ .
Do AB = AC = nên ∆ABC vuông cân tại A
⇒ .
Vậy tam giác ABC, có AB = AC = , BC = , và .
Bài 8 trang 45 Toán lớp 10 Tập 2: Cho hai điểm A(1; 3), B(4; 2).
a) Tìm tọa độ điểm D nằm trên trục Ox sao cho DA = DB.
c) Chứng minh rằng OA vuông góc với AB và từ đó tính diện tích tam giác OAB.
Lời giải:
a) Vì D thuộc trục Ox nên tung độ của D bằng 0. Gọi D(d; 0).
Ta có: = (d – 1; -3) ⇒ AD = ;
= (d – 4; -2) ⇒ BD = ;
Vì AD = BD nên
⇒ d2 – 2d + 10 = d2 – 8d + 20
⇒ 6d = 10
⇒ d =
Vậy .
b) Ta có: = (1; 3) ⇒ OA = ;
= (4; 2) ⇒ OB = ;
= (3; -1) ⇒ AB = .
Chu vi tam giác OAB là:
OA + OB + AB = + + = 2+
Vậy chu vi tam giác OAB là 2+ .
c) Ta có . = 1.3 + 3.(-1) = 3 – 3 = 0.
Do đó OA ⊥ AB
Suy ra tam giác OAB vuông tại A.
Diện tích tam giác OAB là:
.OA.AB = .
Vậy diện tích tam giác OAB là 5.
Bài 9 trang 45 Toán lớp 10 Tập 2: Tính góc giữa hai vectơ và trong các trường hợp sau:
Lời giải:
a) Áp dụng công thức tính góc giữa hai vectơ và , ta có:
cos(; ) =
⇒ (; ) = 90°
Vì vậy góc giữa hai vectơ và bằng 90°.
b) Áp dụng công thức tính góc giữa hai vectơ và , ta có:
cos(; ) =
⇒ (; ) = 45°
Vì vậy góc giữa hai vectơ và bằng 45°.
c) Áp dụng công thức tính góc giữa = (-2; -), = (3; ), ta được:
cos(; ) =
⇒ (; ) = 150°
Vì vậy góc giữa hai vectơ và bằng 150°.
Lời giải:
Ta có = (1; 7) ⇒ AB = ;
= (-7; 1) ⇒ AD = ;
= (1; 7) ⇒ DC = .
= (-7; 1) ⇒ BC = .
Khi đó AB = AD = DC = BC nên ABCD là hình thoi.
Ta lại có: . = 1.(-7) + 7.1 = 0
Suy ra AB ⊥ AD hay .
Vậy ABCD là hình vuông.
Lời giải:
Vectơ tổng hai vận tốc và là:
= (-222; -46)
Khi đó độ dài của hai vectơ là 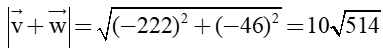
Vậy độ dài tổng hai vẫn tốc và là (km).
Xem thêm lời giải bài tập SGK Toán lớp 10 Chân trời sáng tạo hay, chi tiết khác:
Bài 2: Đường thẳng trong mặt phẳng toạ độ