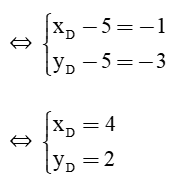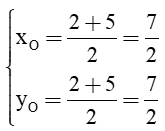Cho ba điểm A(2; 2), B(3; 5), C(5; 5). a) Tìm tọa độ điểm D sao cho ABCD là một hình bình hành
779
13/06/2023
Bài 6 trang 45 Toán lớp 10 Tập 2: Cho ba điểm A(2; 2), B(3; 5), C(5; 5).
a) Tìm tọa độ điểm D sao cho ABCD là một hình bình hành.
b) Tìm tọa độ giao điểm hai đường chéo của một hình bình hành ABCD.
c) Giải tam giác ABC.
Trả lời
a) Gọi D(xD; yD)
Ta có: = (-1; -3);
Để ABCD là một hình bình hành thì
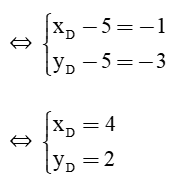
Vậy D(4; 2).
b) Gọi O là giao điểm hai đường chéo của hình bình hành ABCD. Suy ra O là trung điểm của AC.
Khi đó tọa độ điểm O là: 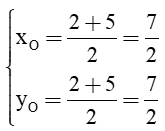
⇒ O.
Vậy O.
c) Ta có: (-1; -3) ⇒ BA = .
(-3; -3) ⇒ CA = .
(2; 0) ⇒ BC = .
Áp dụng định lí cosin, ta có:
cosA =
⇒ ≈ 26,56°
⇒ sinA =
Áp dụng định lí sin, ta có:
⇒ = 45°.
Ta lại có:
Vậy BA = , CA , BC = 2, ≈ 26,56°, , = 45°.
Xem thêm lời giải bài tập SGK Toán lớp 10 Chân trời sáng tạo hay, chi tiết khác:
Bài 3: Nhị thức Newton
Bài tập cuối chương 8
Bài 1: Toạ độ của vectơ
Bài 2: Đường thẳng trong mặt phẳng toạ độ
Bài 3: Đường tròn trong mặt phẳng toạ độ
Bài 4: Ba đường conic trong mặt phẳng tọa độ