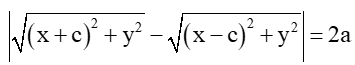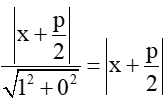Giải SGK Toán 10 (Chân trời sáng tạo) Bài 4: Ba đường conic trong mặt phẳng tọa độ

Giải Toán 10 Bài 4: Ba đường conic trong mặt phẳng tọa độ

1. Elip

Hoạt động khám phá 1 trang 64 Toán lớp 10 Tập 2: Lấy một tấm bìa, ghim hai cái đỉnh lên đó tại hai điểm F₁ và F₂. Lấy một vòng dây kín không đàn hồi có độ dài lớn hơn hai lần đoạn F₁F₂. Quàng vòng dây đó qua hai chiếc đinh và kéo căng tại một điểm M nào đó. Tựa đầu bút chì vào trong vòng dây tại điểm M rồi di chuyển sao cho dây luôn luôn căng. Đầu bút chì vạch lên tấm bìa một đường mà ta gọi là đường elip. Cho biết 2c là khoảng cách F₁F₂ và 2a + 2c là độ dài của vòng dây. Tính tổng hai khoảng cách F₁M và F₂M.

Lời giải:

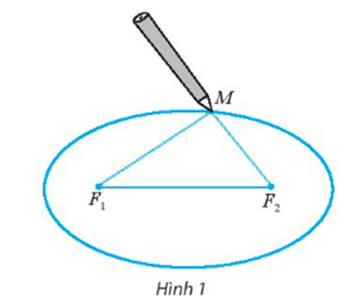
Ta có F₁M + F₂M + F₁F₂ là độ dài sợi dây

Do đó F₁M + F₂M + F₁F₂ = 2a + 2c

⇔ F₁M + F₂M = 2a + 2c – F₁F₂

⇔ F₁M + F₂M = 2a + 2c – 2c

⇔ F₁M + F₂M = 2a.

Vậy F₁M + F₂M = 2a.

Hoạt động khám phá 2 trang 64 Toán lớp 10 Tập 2: Cho Elip (E) có các tiêu điểm F₁ và F₂ và đặt F₁F₂ = c. Chọn hệ trục tọa độ Oxy sao cho F₁(-c; 0) và F₂(c; 0). Xét điểm M(x; y).

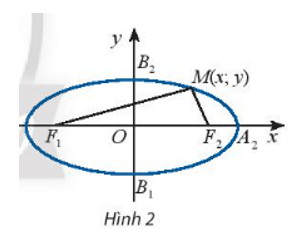
a) Tính F₁M và F₂M theo x, y và c.

b) Giải thích phát biểu sau:

M(x; y) ∈ (E) ⇔ $\sqrt{{\left(x+c\right)}^2+y^2}+\sqrt{{\left(x-c\right)}^2+y^2}=2a$.

Lời giải:

a) Ta có: $\overrightarrow{F_{1}M}\left(x+c;y\right)$ ⇒ $F_{1}M=\sqrt{{\left(x+c\right)}^2+y^2}$

$\overrightarrow{F_{2}M}\left(x-c;y\right)$ ⇒ $F_{2}M=\sqrt{{\left(x-c\right)}^2+y^2}$

Vậy $F_{1}M=\sqrt{{\left(x+c\right)}^2+y^2}$ và $F_{2}M=\sqrt{{\left(x-c\right)}^2+y^2}$.

b)

+) Ta có: Elip (E) là tập hợp các điểm M trong mặt phẳng sao cho F₁M + F₂M = 2a.

Nếu M thuộc elip (E) thì F₁M + F₂M = 2a hay $\sqrt{{\left(x+c\right)}^2+y^2}+\sqrt{{\left(x-c\right)}^2+y^2}=2a$.

+) Nếu điểm M(x; y) có tọa độ thỏa mãn $\sqrt{{\left(x+c\right)}^2+y^2}+\sqrt{{\left(x-c\right)}^2+y^2}=2a$ hay F₁M + F₂M = 2a thì M là điểm thỏa mãn F₁M + F₂M = 2a.

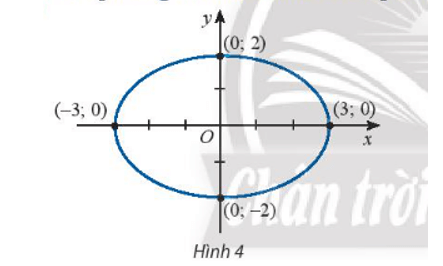
Thực hành 1 trang 65 Toán lớp 10 Tập 2: Viết phương trình chính tắc của elip trong Hình 4.

Lời giải:

+) Hình 4:

Ta có: a = 3, b = 2

Khi đó phương trình chính tắc của elip là:

$\frac{x^2}{3^2}+\frac{y^2}{2^2}=1$

⇔ $\frac{x^2}{9}+\frac{y^2}{4}=1$

Vậy phương trình chính tắc của elip là: $\frac{x^2}{9}+\frac{y^2}{4}=1$.

Vận dụng 1 trang 65 Toán lớp 10 Tập 2: Một đường hầm có mặt cắt hình nửa elip cao 4m, rộng 10m (Hình 5). Viết phương trình chính tắc của elip đó.

Lời giải:

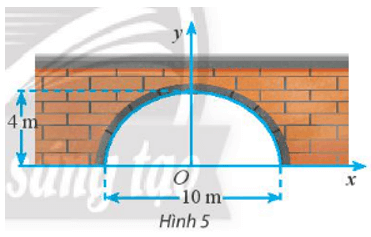
Theo hình vẽ ta thấy: 2a = 10 ⇔ a = 5 và b = 4.

Khi đó phương trình chính tắc của elip là:

$\frac{x^2}{5^2}+\frac{y^2}{4^2}=1$

⇔ $\frac{x^2}{25}+\frac{y^2}{16}=1$.

Vậy phương trình chính tắc của elip cần tìm là: $\frac{x^2}{25}+\frac{y^2}{16}=1$.

2. Hypebol

Hoạt động khám phá 3 trang 65 Toán lớp 10 Tập 2: Lấy một tấm bìa, trên đó đánh dấu hai điểm F₁ và F₂. Lấy một cây thước thẳng với mép thước AB có chiều dài d và một đoạn dây không đàn hồi có chiều dài l sao cho d – l = 2a nhỏ hơn khoảng cách F₁F₂ (Hình 6a).

Đính một đầu dây vào đầu A của thước, dùng đinh ghim đầu dây còn lại vào điểm F₂. Đặt thước sao cho đầu B của thước trùng với điểm F₁ và đoạn thẳng BA có thể quay quanh F₁. Tựa đầu bút chì M vào đoạn dây, di chuyển điểm M trên tấm bìa và giữ sao cho dây luôn căng, đoạn AM ép sát vào thước, khi đó M sẽ vạch ra trên tấm bìa một đường (H) (xem Hình 6b).

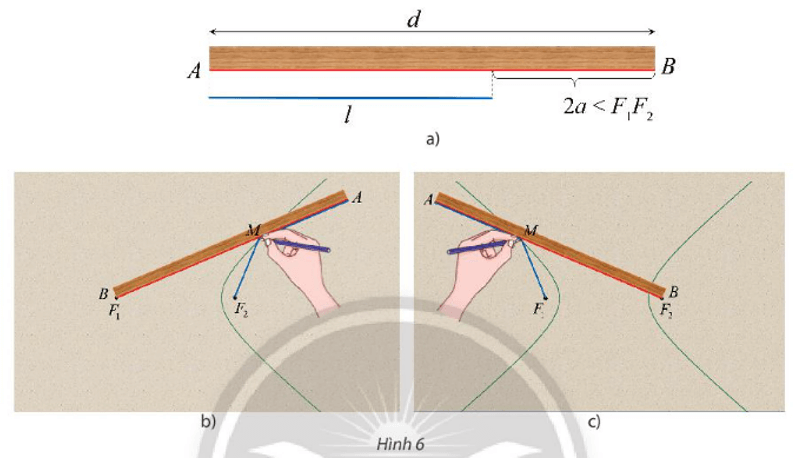
a) Chứng tỏ rằng khi M di động, ta luôn có MF₁ – MF₂ = 2a.

b) Vẫn đính một đầu dây vào đầu A của thước nhưng đổi chỗ cố định đầu dây còn lại vào F₁, đầu B của thước trùng với F₂ sao cho đoạn thẳng BA có thể quay quanh F₂ và làm tương tự như lần đầu để đầu bút chì M vẽ được một nhánh khác của đường H (Hình 6c). Tính MF₂ – MF₁.

Lời giải:

a) Ta có:

MF₁ + MA = AB = d (1)

MF₂ + MA = l (2)

Lấy vế với vế của (1) trừ cho (2) ta được: (MF₁ + MA) – (MF₂ + MA) = d – l

⇔ MF₁ + MA – MF₂ – MA = d – l

⇔ MF₁ – MF₂ = d – l

Mà d – l = 2a.

⇒ MF₁ – MF₂ = 2a.

Vậy MF₁ – MF₂ = 2a.

b) Ta có:

MF₂ + MA = AB = d (3)

MF₁ + MA = l (4)

Lấy vế với vế của (3) trừ cho (4) ta được: (MF₂ + MA) – (MF₁ + MA) = d – l

⇔ MF₂ + MA – MF₁ – MA = d – l

⇔ MF₂ – MF₁ = d – l

Mà d – l = 2a.

⇒ MF₂ – MF₁ = 2a.

Vậy MF₂ – MF₁ = 2a.

Hoạt động khám phá 4 trang 66 Toán lớp 10 Tập 2: Cho hypebol (H) có các tiêu điểm F₁ và F₂ và đặt F₁F₂ = 2c. Điểm M thuộc hypecbol (H) khi và chỉ khi |F₁M – F₂M| = 2a. Chọn hệ trục tọa độ Oxy sao cho F₁(-c; 0) và F₂(c; 0). Xét điểm M(x; y).

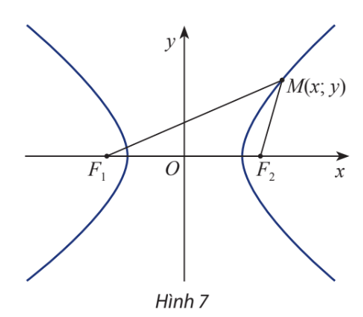
a) Tính F₁M và F₂M theo x, y và c.

b) Giải thích các phát biểu sau:

M(x; y) ∈ (H) ⇔ 

Lời giải:

a) Ta có: $\overrightarrow{F_{1}M}\left(x+c;y\right)$ ⇒ $F_{1}M=\sqrt{{\left(x+c\right)}^2+y^2}$

$\overrightarrow{F_{2}M}\left(x-c;y\right)$ ⇒ $F_{2}M=\sqrt{{\left(x-c\right)}^2+y^2}$

Vậy $F_{1}M=\sqrt{{\left(x+c\right)}^2+y^2}$ và $F_{2}M=\sqrt{{\left(x-c\right)}^2+y^2}$.

b) +) Ta có: Elip (E) là tập hợp các điểm M trong mặt phẳng sao cho F₁M + F₂M = 2a.

Nếu M thuộc elip (E) thì F₁M + F₂M = 2a hay $\sqrt{{\left(x+c\right)}^2+y^2}+\sqrt{{\left(x-c\right)}^2+y^2}=2a$.

+) Nếu điểm M(x; y) có tọa độ thỏa mãn $\sqrt{{\left(x+c\right)}^2+y^2}+\sqrt{{\left(x-c\right)}^2+y^2}=2a$ hay F₁M + F₂M = 2a thì M là điểm thỏa mãn F₁M + F₂M = 2a.

Thực hành 2 trang 67 Toán lớp 10 Tập 2: Viết phương trình chính tắc của hypebol có tiêu cự bằng 10 và độ dài trục ảo bằng 6.

Lời giải:

Tiêu cự của hypebol là: 2c = 10 ⇔ c = 5 và độ dài trục ảo là 2b = 6 ⇔ b = 3.

Ta có: $\sqrt{a^2+b^2}=c$

⇔ a² + b² = c²

⇔ a² = c² – b² = 5² – 3² = 25 – 9 = 16

⇔ a = 4

Khi đó phương trình chính tắc của hypebol có tiêu cự bằng 10 và độ dài trục ảo bằng 6 là:

$\frac{x^2}{4^2}-\frac{y^2}{3^2}=1$

⇔ $\frac{x^2}{16}-\frac{y^2}{9}=1$.

Vậy phương trình chính tắc của hypebol cần tìm là: $\frac{x^2}{16}-\frac{y^2}{9}=1$.

Vận dụng 2 trang 67 Toán lớp 10 Tập 2: Một tháp làm nguội của một nhà máy có mặt cắt là một hypebol có phương trình $\frac{x^2}{{27}^2}-\frac{y^2}{{40}^2}=1$ (Hình 9). Cho biết chiều cao của tháp là 120m và khoảng cách từ nóc tháp đến tâm đối xứng của hypebol bằng một nửa khoảng cách từ tâm đối xứng đến đáy. Tính bán kính đường tròn nóc và bán kính đường tròn đáy của tháp.

Lời giải:

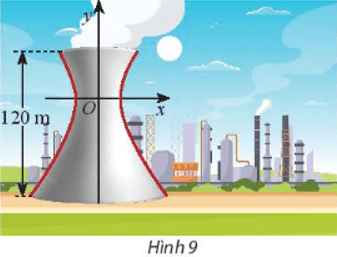
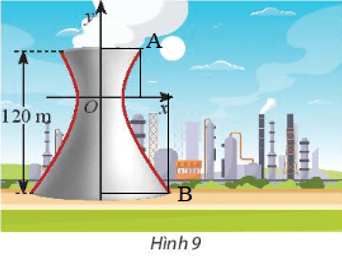
Gọi khoảng cách từ nóc tháp đến tâm đối xứng của hypebol là h thì khoảng cách từ tâm đối xứng đến đáy là 2h.

Khi đó chiều cao của tháp là: h + 2h = 3h

Mà chiều cao của tháp là 120m nên ta có: 3h = 120 ⇔ h = 120 : 3 = 40 (m).

Gọi A và B là hai điểm như hình vẽ.

Ta có khoảng cách từ nóc tháp đến tâm đối xứng của hypebol cũng chính là khoảng cách từ điểm A đến trục hoành hay là tung độ của điểm A.

⇒ y_A = 40.

Vì A thuộc hypebol nên tọa độ điểm A thỏa mãn phương trình $\frac{x^2}{{27}^2}-\frac{y^2}{{40}^2}=1$

⇒ $\frac{x_A^2}{{27}^2}-\frac{y_A^2}{{40}^2}=1$

⇔ $\frac{x_A^2}{{27}^2}-\frac{{40}^2}{{40}^2}=1$

⇔ $\frac{x_A^2}{{27}^2}-1=1$

⇔ $\frac{x_A^2}{{27}^2}=2$

⇔ $x_A^2={2.27}^2$

⇔ $x_A=27\sqrt{2}$

⇒ $A\left(27\sqrt{2};40\right)$

Mặt khác điểm A thuộc đường tròn nóc nên khoảng cách từ A đến tâm đường tròn là bán kính của đường tròn và bằng 27$\sqrt{2}$.

Ta có khoảng cách từ nóc tháp đến tâm đối xứng của hypebol cũng chính là khoảng cách từ điểm B đến trục hoành hay là tung độ của điểm B.

⇒ y_B = 2h = 2.40 = 80.

Vì B thuộc hypebol nên tọa độ điểm B thỏa mãn phương trình $\frac{x^2}{{27}^2}-\frac{y^2}{{40}^2}=1$

⇒ $\frac{x_B^2}{{27}^2}-\frac{y_B^2}{{40}^2}=1$

⇔ $\frac{x_B^2}{{27}^2}-\frac{{80}^2}{{40}^2}=1$

⇔ $\frac{x_B^2}{{27}^2}-4=1$

⇔ $\frac{x_B^2}{{27}^2}=5$

⇔ $x_B^2={5.27}^2$

⇔ $x_B=27\sqrt{5}$

⇒ $B\left(27\sqrt{5};80\right)$

Mặt khác điểm B thuộc đường tròn nóc nên khoảng cách từ B đến tâm đường tròn là bán kính của đường tròn và bằng 27$\sqrt{5}$.

Vậy bán kính đường tròn nóc là 27$\sqrt{2}$ và bán kính đường tròn đáy là 27$\sqrt{5}$.

3. Parabol

Hoạt động khám phá 5 trang 68 Toán lớp 10 Tập 2: Trong mặt phẳng Oxy, cho điểm $F\left(0;\frac{1}{2}\right)$, đường thẳng ∆: y + $\frac{1}{2}$ = 0 và điểm M(x; y). Để tìm hệ thức giữa x và y sao cho M cách đều F và ∆, một học sinh đã làm như sau:

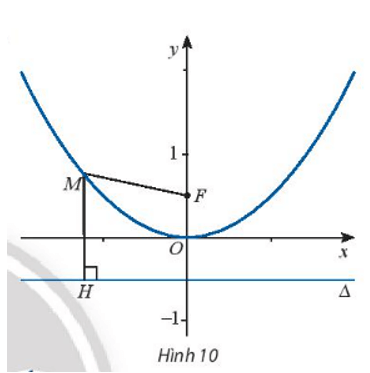
- Tính MF và MH (với H là hình chiếu của M lên ∆):

MF = $\sqrt{x^2+{\left(y-\frac{1}{2}\right)}^2}$ , MH = .

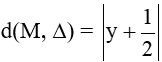
- Điều kiện để M cách đều F và ∆:

MF = d(M, ∆) ⇔

⇔ $x^2+{\left(y-\frac{1}{2}\right)}^2={\left(y+\frac{1}{2}\right)}^2$

⇔ x² = 2y

⇔ y = $\frac{1}{2}$x² (*)

Hãy cho biết tên đồ thị (P) của hàm số (*) vừa tìm được.

Lời giải:

Hàm số (*) vừa tìm được là hàm bậc hai và đồ thị của hàm số (*) là hàm Parabol.

Hoạt động khám phá 6 trang 68 Toán lớp 10 Tập 2: Cho parabol (P) có tiêu điểm F và đường chuẩn ∆. Gọi khoảng cách từ tiêu điểm đến đường chuẩn là p, hiển nhiên p > 0.

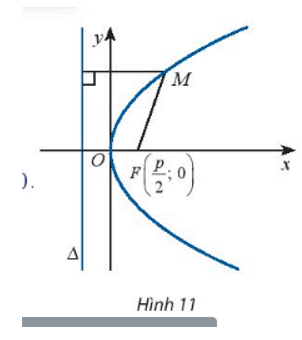
Chọn hệ trục tọa độ Oxy sao cho $F\left(\frac{p}{2};0\right)$ và ∆: x + $\frac{p}{2}$ = 0. Xét điểm M(x; y).

a) Tính MF và d(M. ∆).

b) Giải thích phát biểu sau:

M(x; y) ∈ (P) ⇔ .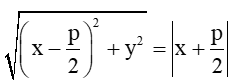

Lời giải:

a) Ta có: $\overrightarrow{FM}=\left(x-\frac{p}{2};y\right)$ ⇒ MF = $\sqrt{{\left(x-\frac{p}{2}\right)}^2+y^2}$

Khoảng cách từ điểm M đến đường thẳng ∆ là:

d(M, ∆) = 

b) +) Ta có M(x; y) ∈ (P) cần chứng minh .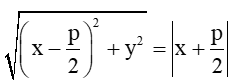

Vì M(x; y) ∈ (P) nên M cách đều F và ∆

⇒ MF = d(M, ∆) hay 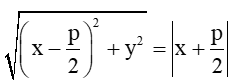 (1).

+) Ta có điểm M(x; y) thỏa mãn 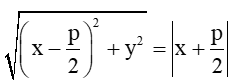 thì M(x; y) ∈ (P).

Ta có 

⇒ MF = d(M, ∆)

Nghĩa là điểm M thỏa mãn cách đều tiêu điểm F và đường chuẩn ∆. Do đó điểm M thuộc parabol (P) (2)

Từ (1) và (2) suy ra điều phải chứng minh.

Thực hành 3 trang 70 Toán lớp 10 Tập 2: Viết phương trình chính tắc của parabol (P) có đường chuẩn ∆: x + 1 = 0.

Lời giải:

Ta có đường chuẩn ∆: x + 1 = 0 nên $\frac{p}{2}=1$ ⇔ p = 2.

Khi đó phương trình chính tắc của parabol (P) là: y² = 2px

⇔ y² = 2.2.x

⇔ y² = 4x.

Vậy phương trình chính tắc của parabol cần tìm là y² = 4x.

Vận dụng 3 trang 70 Toán lớp 10 Tập 2: Một cổng chào có hình parabol cao 10m và bề rộng của cổng tại chân cổng là 5m. Tính bề rộng của cổng tại chỗ cách đỉnh 2m.

Lời giải:

Ta vẽ parabol biểu diễn cho cổng chào như sau:

Gọi phương trình của parabol là y² = 2px.

Ta có chiều cao của cổng là OH = 10, bề rộng của cổng là AB = 5.

Khi đó A(10; 2,5), thay tọa độ điểm A vào parabol y² = 2px, ta được:

2,5² = 2p.10

⇔ $\frac{25}{4}$ = 20p

⇔ p = $\frac{25}{4.20}=\frac{5}{16}$

Suy ra parabol có phương tình y² = 2.$\frac{5}{16}$.x ⇔ y² = $\frac{5}{8}$.x

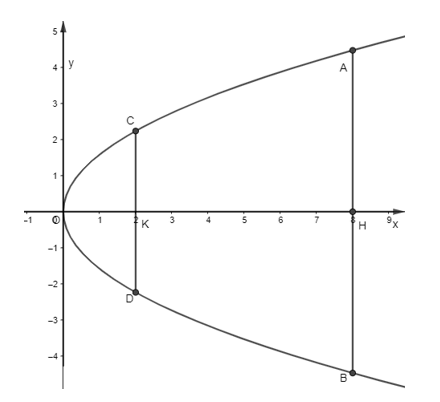
Tại vị trí điểm K cách đỉnh 2m bề rộng của cổng là đoạn CD.

Gọi C(2; y_C) (y_C > 0)

Vì C thuộc parabol nên tọa độ của C thỏa mãn y² = $\frac{5}{8}$.x nên ta có:

$y_C^2$ = $\frac{5}{8}$.2

⇔ $y_C^2$ = $\frac{5}{4}$

⇔ y_C = $\frac{\sqrt{5}}{2}$

⇒ C = (0; $\frac{\sqrt{5}}{2}$).

Khi đó CD = 2|y_C|= 2.$\frac{\sqrt{5}}{2}$ = $\sqrt{5}$ .

Vậy bề rộng của cộng tại chỗ cách đỉnh 2m là $\sqrt{5}$m.

Bài tập

Bài 1 trang 70 Toán lớp 10 Tập 2: Viết phương trình chính tắc của:

a) Elip có trục lớn bằng 20 và trục nhỏ bằng 16;

b) Hypebol có tiêu cự 2c = 20 và độ dài trục thực 2a = 12;

c) Parabol có tiêu điểm F$\left(\frac{1}{2};0\right)$.

Lời giải:

a) Độ dài trục lớn của elip là 2a = 20 ⇔ a = 20 : 2 = 10;

Độ dài trục nhỏ của elip là: 2b = 16 ⇔ b = 16 : 2 = 8;

Khi đó phương trình chính tắc của elip cần tìm là:

$\frac{x^2}{{10}^2}+\frac{y^2}{8^2}=1$

⇔ $\frac{x^2}{100}+\frac{y^2}{64}=1$

Vậy phương trình chính tắc của elip là: $\frac{x^2}{100}+\frac{y^2}{64}=1$.

b) Ta có tiêu cự của hypebol là 2c = 20 ⇔ c = 20 : 2 = 10;

Độ dài trục thực 2a = 12 ⇔ a = 12 : 2 = 6;

Ta lại có: a² + b² = c²

⇔ b² = c² – a²

⇔ b² = 10² – 6²

⇔ b² = 100 – 36

⇔ b² = 64

⇔ b = 8

Khi đó phương trình chính tắc của elip là: $\frac{x^2}{6^2}-\frac{y^2}{8^2}=1\iff \frac{x^2}{36}-\frac{y^2}{64}=1$

c) Parabol có tiêu điểm F$\left(\frac{1}{2};0\right)$ nghĩa là $\frac{p}{2}=\frac{1}{2}$ ⇔ p = 1.

Khi đó phương trình chính tắc của parabol là: y² = 2.1.x ⇔ y² = 2x.

Bài 2 trang 70 Toán lớp 10 Tập 2: Viết phương trình chính tắc của các đường conic dưới đây. Gọi tên và tìm tọa độ các tiêu điểm của chúng.

a) (C₁): 4x² + 16y² = 1;

b) (C₂): 16x² – 4y² = 144;

c) (C₃): x= $\frac{1}{8}$y².

Lời giải:

a) Xét phương trình: 4x² + 16y² = 1

⇔ $\frac{x^2}{\frac{1}{4}}+\frac{y^2}{\frac{1}{16}}=1$

⇔ $\frac{x^2}{{\left(\frac{1}{2}\right)}^2}+\frac{y^2}{{\left(\frac{1}{4}\right)}^2}=1$

Đây là phương trình chính tắc của elip với a = $\frac{1}{2}$ và b = $\frac{1}{4}$.

Ta có: b² + c² = a²

⇔ c² = ${\left(\frac{1}{2}\right)}^2-{\left(\frac{1}{4}\right)}^2=\frac{1}{4}-\frac{1}{16}=\frac{3}{16}$

⇔ c = $\frac{\sqrt{3}}{4}$

Khi đó tọa độ các tiêu điểm của elip là F₁$\left(\frac{\sqrt{3}}{4};0\right)$ và F₂$\left(-\frac{\sqrt{3}}{4};0\right)$.

Vậy phương trình đã cho biểu diễn cho elip và có tọa độ các tiêu điểm lần lượt là F₁$\left(\frac{\sqrt{3}}{4};0\right)$ và F₂$\left(-\frac{\sqrt{3}}{4};0\right)$.

b) Xét phương trình 16x² – 4y² = 144

⇔ $\frac{16x^2}{144}-\frac{4y^2}{144}=1$

⇔ $\frac{x^2}{\frac{144}{16}}-\frac{y^2}{\frac{144}{4}}=1$

⇔ $\frac{x^2}{3^2}-\frac{y^2}{6^2}=1$

Đây là phương trình chính tắc của hypebol với a = 3 và b = 6.

Ta có: a² + b² = c²

⇔ c² = 3² + 6² = 9 + 36 = 45

⇔ c = $3\sqrt{5}$

Khi đó tọa độ các tiêu điểm của hypebol là F₁$\left(3\sqrt{5};0\right)$ và F₂$\left(-3\sqrt{5};0\right)$.

Vậy phương trình đã cho biểu diễn cho hypebol và có tọa độ các tiêu điểm lần lượt là F₁$\left(3\sqrt{5};0\right)$ và F₂$\left(-3\sqrt{5};0\right)$.

c) Ta có: x= $\frac{1}{8}$y²⇔ y² = 8x

Ta thấy phương trình (C₃) có dạng y² = 2px nên (C₃) là phương trình của parabol và p = 4.

⇒ Tọa độ tiêu điểm của (C₃) là F(2; 0).

Vậy parabol (C₃): x= $\frac{1}{8}$y² có tiêu điểm là F = (2; 0).

Bài 3 trang 70 Toán lớp 10 Tập 2: Để cắt một bảng hiệu quảng cáo hình elip có trục lớn là 80 cm và trục nhỏ là 40 cm từ một tấm ván ép hình chữ nhật có kích thước 80 cm × 40 cm, người ta vẽ hình elip đó lên ván ép như hướng dẫn sau:

Chuẩn bị:

- Hai cái đinh, một vòng dây kín không đàn hồi, bút chì.

Thực hiện:

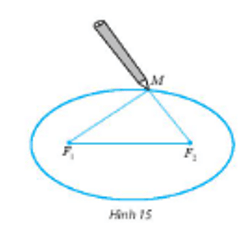
- Xác định vị trí (hai tiêu điểm của elip) và ghim hai cái đinh lên hai điểm đó trên tấm ván.

- Quàng vòng dây qua hai chiếc đinh và kéo căng tại một điểm M nào đó. Tựa đầu bút chì vào trong vòng dây tại điểm M rồi di chuyển sao cho dây luôn căng. Đầu bút chì vạch lên tấm bìa một đường elip. (xem minh họa trong Hình 15).

Phải ghim hai cái đinh cách các mép tấm ván ép bao nhiêu xentimét và lấy vòng dây có độ dài là bao nhiêu?

Lời giải:

Ta có: hình elip có độ dài trục lớn là 80 cm nên 2a = 80 ⇔ a = 40

Độ dài trục nhỏ là 40 cm nên 2b = 40 ⇔ b = 20

⇒ c = $\sqrt{a^2-b^2}$ = $\sqrt{{40}^2-{20}^2}$= $20\sqrt{3}$(cm).

⇒ 2c = 2.20$\sqrt{3}$= 40$\sqrt{3}$

⇒ F₁F₂ = 2c = 40$\sqrt{3}$

Do đó hai cái đinh cách mép chiều dài của tấm ván là 20 cm, cách mép chiều rộng của tấm ván là (80 − $40\sqrt{3}$) : 2 ≈5,36 cm.

Độ dài vòng dây là MF₁ + MF₂ + F₁F₂ = 2a + 2c = 2.40 + 2.$20\sqrt{3}$ ≈ 74,64 cm.

Vậy hai cái đinh cách mép chiều dài của tấm ván khoảng 20 cm, cách mép chiều rộng của tấm ván 5,36 cm và Độ dài vòng dây là 74,64 cm.

Bài 4 trang 71 Toán lớp 10 Tập 2: Một nhà vòm chứa máy bay có mặt cắt hình nửa elip cao 8m, rộng 20m (Hình 16).

a) Chọn hệ tọa độ thích hợp và viết phương trình của elip nói trên.

b) Tính khoảng cách theo phương thẳng đứng từ một điểm cách chân tường 5m lên nóc nhà vòm

Lời giải:

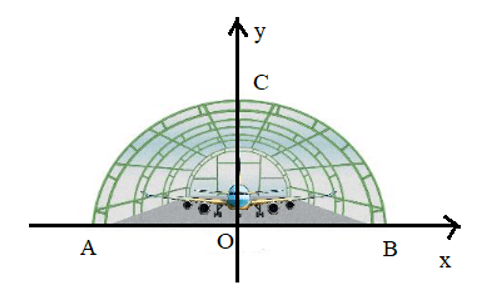
Đặt hệ trục tọa độ như sau:

Theo hình vẽ ta thấy AB là độ dài trục lớn của elip và cũng chính là chiều rộng của nhà vòm nên 2a = 20 ⇔ a = 10.

OC là một nửa trục bé hay chính là chiều cao của nhà vòm nên b = 8.

Khi đó phương trình của elip trên là:

$\frac{x^2}{{10}^2}+\frac{y^2}{8^2}=1$

⇔ $\frac{x^2}{100}+\frac{y^2}{64}=1$ (*)

Vậy phương trình elip đã cho là $\frac{x^2}{100}+\frac{y^2}{64}=1$.

b) Gọi điểm D là điểm nằm trên elip và cách chân tường 5m.

Khi đó khoảng cách từ D đến gốc tọa độ O là 10 – 5 = 5m. Hay chính là hoành độ của điểm D.

Gọi D(5; y_D)

Vi D thuộc elip trên nên tọa độ điểm D thỏa mãn phương trình (*), ta có:

$\frac{5^2}{100}+\frac{y_D^2}{64}=1$

⇔ $\frac{y_D^2}{64}=\frac{3}{4}$

⇔ $y_D^2=48$

⇔ y_D = $4\sqrt{3}$

⇒ D(5; $4\sqrt{3}$)

Suy ra khoảng cách theo phương thẳng đứng từ một điểm cách chân tường 5m đến nóc nhà là tung độ của điểm D là $4\sqrt{3}$(m).

Vậy khoảng cách theo phương thẳng đứng từ một điểm cách chân tường 5m đến nóc nhà là $4\sqrt{3}$m.

Bài 5 trang 71 Toán lớp 10 Tập 2: Một tháp làm nguội của một nhà máy có mặt cắt là hình hypebol có phương trình $\frac{x^2}{{28}^2}-\frac{y^2}{{42}^2}=1$(Hình 17). Biết chiều cao của tháp là 150m và khoảng cách từ nóc tháp đến tâm đối xứng của hypebol bằng $\frac{2}{3}$ khoảng cách từ tâm đối xứng đến đáy. Tính bán kính nóc và bán kính đáy của tháp.

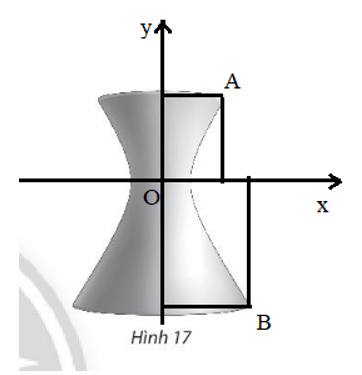
Lời giải:

Đặt hệ trục tọa độ như hình vẽ, điểm O là tâm đối xứng của hypebol:

Gọi hai điểm A và B như hình vẽ.

Đặt khoảng cách từ tâm đối xứng đến đáy là h. Khi đó khoảng cách từ nóc tháp đến tâm đối xứng là $\frac{2}{3}$h.

Theo đầu bài ta có: h + $\frac{2}{3}$h = 150

⇔ $\frac{5}{3}$h = 150

⇔ h = 150 : $\frac{5}{3}$

⇔ h = 90.

Ta có khoảng cách từ nóc tháp đến tâm đối xứng của hypebol cũng chính là khoảng cách từ điểm A đến trục hoành hay là tung độ của điểm A.

⇒ y_A = $\frac{2}{3}$h = $\frac{2}{3}$.90 = 60.

Vì A thuộc hypebol nên tọa độ điểm A thỏa mãn phương trình $\frac{x^2}{{28}^2}-\frac{y^2}{{42}^2}=1$

⇒ $\frac{x_A^2}{{28}^2}-\frac{y_A^2}{{42}^2}=1$

⇔ $\frac{x_A^2}{{28}^2}-\frac{{60}^2}{{42}^2}=1$

⇔ $\frac{x_A^2}{{28}^2}-\frac{100}{49}=1$

⇔ $\frac{x_A^2}{{28}^2}=\frac{149}{49}$

⇔ $x_A^2=2384$

⇔ $x_A=4\sqrt{149}$

⇒ $A\left(4\sqrt{149};60\right)$

Mặt khác điểm A thuộc đường tròn nóc nên khoảng cách từ A đến tâm đường tròn là bán kính của đường tròn và bằng $4\sqrt{149}$.

Ta có khoảng cách từ nóc tháp đến tâm đối xứng của hypebol cũng chính là khoảng cách từ điểm B đến trục hoành hay là tung độ của điểm B.

⇒ y_B = -h = -90.

Vì B thuộc hypebol nên tọa độ điểm B thỏa mãn phương trình $\frac{x^2}{{28}^2}-\frac{y^2}{{42}^2}=1$

⇒ $\frac{x_B^2}{{28}^2}-\frac{y_B^2}{{42}^2}=1$

⇔ $\frac{x_B^2}{{28}^2}-\frac{{\left(-90\right)}^2}{{42}^2}=1$

⇔ $\frac{x_B^2}{{28}^2}-\frac{225}{49}=1$

⇔ $\frac{x_B^2}{{28}^2}=\frac{274}{49}$

⇔ $x_B^2=4384$

⇔ $x_B=4\sqrt{274}$

⇒ $B\left(4\sqrt{274};90\right)$

Mặt khác điểm B thuộc đường tròn nóc nên khoảng cách từ B đến tâm đường tròn là bán kính của đường tròn và bằng $4\sqrt{274}$.

Vậy bán kính đường tròn nóc là $4\sqrt{149}$ và bán kính đường tròn đáy là $4\sqrt{274}$.

Bài 6 trang 71 Toán lớp 10 Tập 2: Một cái cầu có dây cáp treo hình parabol, cầu dài 100m và được nâng đỡ bởi những thanh thẳng đứng treo từ cáp xuống, thanh dài nhất là 30m, thanh ngắn nhất là 6m (Hình 18). Tính chiều dài của thanh cách điểm giữa cầu 18m.

Lời giải:

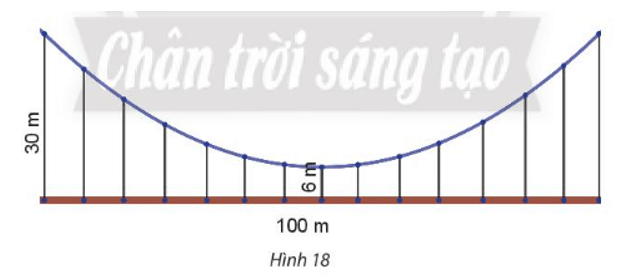
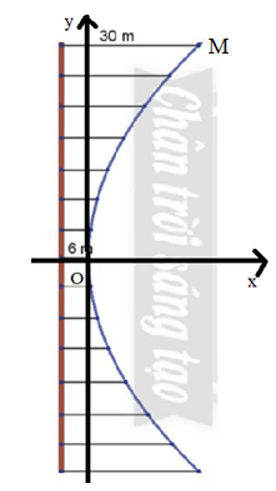
Ta chọn hệ tọa độ sao cho parabol có phương trình: y² = 2px.

Thay điểm M(24; 50) vào phương trình trên ta được:

50² = 2p.24

⇔ p = $\frac{2500}{48}=\frac{625}{12}$

Khi đó phương trình parabol là: y² = $\frac{625}{6}$x

Gọi N là điểm nằm trên parabol cách điểm giữa cầu 18m, nghĩa là N(x_N; 18).

Thay tọa độ điểm N vào parabol ta được:

18² = $\frac{625}{6}$x_N

⇔ x_N = $\frac{1944}{625}\approx 3,11$

Vậy chiều dài của thanh cách điểm giữa cầu 18m là: 3,11 + 6 = 9,11 m.

Thử thách trang 73 Toán lớp 10 Tập 2: Áp dụng tính chất quang học của parabol để giải quyết vấn đề sau đây:

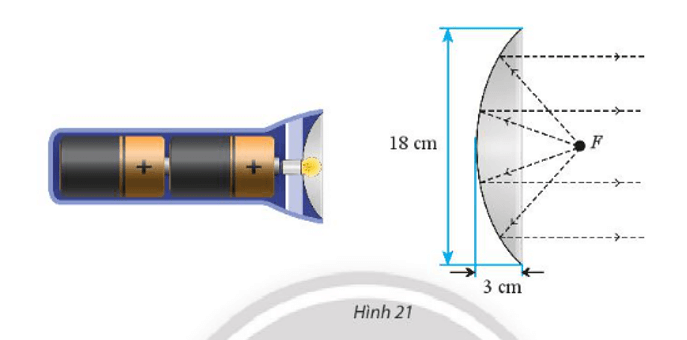
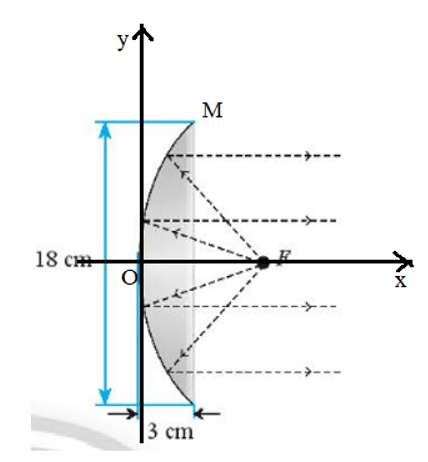
Một chóa đèn pin có mặt cắt hình parabol với kích thước như trong Hình 21.

a) Chọn hệ chục tọa độ Oxy sao cho gốc O là đỉnh của parabol và trục Ox đi qua tiêu điểm. Viết phương trình của parabol trong hệ tọa độ vừa chọn.

b) Để đèn chiếu được xa phải đặt bóng đèn cách đỉnh của chóa đèn bao nhiêu xentimét?

Lời giải:

Đặt hệ trục tọa độ như hình vẽ:

Phương trình parabol cần tìm có dạng y² = 2px.

Điểm M(3; 9) thuộc parabol trên nên ta có:

9² = 2p.3

⇔ 6p = 81

⇔ p = $\frac{81}{6}$

Suy ra phương trình parabol là y² = 2.$\frac{81}{6}$.x ⇔ y² = $\frac{81}{3}$x.

Vậy phương trình parabol cần tìm là y² = $\frac{81}{3}$x.

b) Để đèn chiếu được xa thì phải đặt bóng đèn tại tiêu điểm F của parabol.

Ta có: F = $\left(\frac{p}{2};0\right)=\left(\frac{\frac{81}{6}}{2};0\right)=\left(\frac{81}{12};0\right)$.

Vậy để đèn chiếu được xa thì phải đặt bóng đèn cách đỉnh của chóa đèn $\frac{81}{12}$ xentimét.

Xem thêm lời giải bài tập SGK Toán lớp 10 Chân trời sáng tạo hay, chi tiết khác:

Bài 2: Đường thẳng trong mặt phẳng toạ độ

Bài 3: Đường tròn trong mặt phẳng toạ độ

Bài tập cuối chương 9

Bài 1: Không gian mẫu và biến cố

Bài 2: Xác suất của biến cố