Bộ 20 đề thi học kì 1 Toán 11 năm 2022 - 2023 có đáp án
Bộ 20 đề thi học kì 1 Toán 11 năm 2022 - 2023 có đáp án (Đề 17)
-
862 lượt thi
-
30 câu hỏi
-
0 phút
Danh sách câu hỏi
Câu 1:
 Xem đáp án
Xem đáp án
Đáp án C
Phương pháp:
Giải phương trình lượng giác cơ bản: \[\tan x = \tan \alpha \Leftrightarrow x = \alpha + k\pi \left( {k \in \mathbb{Z}} \right).\]
Cách giải:
\[\tan \frac{x}{4} = - 1 \Leftrightarrow \frac{x}{4} = \frac{{ - \pi }}{4} + k\pi \Leftrightarrow x = - \pi + 4k\pi \left( {k \in \mathbb{Z}} \right)\]
\[x \in \left[ {0;12\pi } \right] \Leftrightarrow 0 \le - \pi + 4k\pi \le 12\pi \Leftrightarrow \frac{1}{4} \le k \le \frac{{13}}{4}\left( {k \in \mathbb{Z}} \right) \Leftrightarrow k \in \left\{ {1;2;3} \right\}.\]
Vậy phương trình đã cho có 3 nghiệm thuộc \[\left[ {0;12\pi } \right]\]
Câu 2:
 Xem đáp án
Xem đáp án
Đáp án A
Phương pháp:
+) Giải phương trình lượng giác cơ bản: \[\sin x = \sin \alpha \Leftrightarrow \left[ \begin{array}{l}x = \alpha + k2\pi \\x = \pi - \alpha + k2\pi \end{array} \right.\left( {k \in \mathbb{Z}} \right),\] sau đó tìm các nghiệm thuộc \[\left[ {0;10\pi } \right]\] của phương trình.
+) Tính tổng các nghiệm: sử dụng công thức tổng n số hạng đầu tiên của CSC: \[{S_n} = \frac{{\left( {{u_1} + {u_n}} \right).n}}{2}.\]
Cách giải:
\[\sin x = 0 \Leftrightarrow x = k\pi \left( {k \in \mathbb{Z}} \right)\]
\[x \in \left[ {0;10\pi } \right] \Leftrightarrow 0 \le k\pi \le 10\pi \Leftrightarrow 0 \le k \le 10 \Leftrightarrow k \in \left\{ {0;1;2;...;10} \right\}\]
Khi đó tổng các nghiệm thuộc \[\left[ {0;10\pi } \right]\] của phương trình trên là:
\[0 + \pi + 2\pi + 3\pi + ... + 10\pi = \left( {0 + 1 + 2 + ... + 10} \right)\pi = \frac{{10.11}}{2}\pi = 55\pi .\]
Câu 3:
 Xem đáp án
Xem đáp án
Đáp án C
Phương pháp:
Giải phương trình lượng giác cơ bản: \[\sin x = \sin \alpha \Leftrightarrow \left[ \begin{array}{l}x = \alpha + k2\pi \\x = \pi - \alpha + k2\pi \end{array} \right.\left( {k \in \mathbb{Z}} \right),\] sau đó tìm các nghiệm thuộc \[x \in \left[ {0;2\pi } \right]\] của phương trình.
Cách giải:
\[\sin x = \frac{{\sqrt 2 }}{2} \Leftrightarrow \left[ \begin{array}{l}x = \frac{\pi }{4} + k2\pi \\x = \frac{{3\pi }}{4} + l2\pi \end{array} \right.\left( {k,l \in \mathbb{Z}} \right).\]
Xét họ nghiệm \[x = \frac{\pi }{4} + k2\pi \in \left[ {0;2\pi } \right]\] ta có: \[0 \le \frac{\pi }{4} + k2\pi \le 2\pi \Leftrightarrow - \frac{1}{8} \le k \le \frac{7}{8} \Leftrightarrow k = 0.\]
Xét họ nghiệm \[x = \frac{{3\pi }}{4} + l2\pi \in \left[ {0;2\pi } \right]\] ta có: \[0 \le \frac{{3\pi }}{4} + l2\pi \le 2\pi \Leftrightarrow - \frac{3}{8} \le l \le \frac{5}{8} \Leftrightarrow l = 0.\]
Vậy phương trình đã cho có 2 nghiệm thuộc \[\left[ {0;2\pi } \right]\] là \[\frac{\pi }{4};\frac{{3\pi }}{4}.\]
Câu 4:
 Xem đáp án
Xem đáp án
Đáp án A
Phương pháp:
Phương trình dạng \[a\sin x + b\cos x = c\] có nghiệm \[ \Leftrightarrow {a^2} + {b^2} \ge {c^2}.\]
Cách giải:
Phương trình \[\sin x - \sqrt 3 m\cos x = 2m\] có nghiệm \[ \Leftrightarrow 1 + {\left( {\sqrt 3 m} \right)^2} \ge \left( {2{m^2}} \right) \Leftrightarrow {m^2} \le 1 \Leftrightarrow - 1 \le m \le 1.\]
Câu 5:
 Xem đáp án
Xem đáp án
Đáp án C
Phương pháp:
\[ - 1 \le \cos x \le 1{\rm{ }}\forall x \in \mathbb{R}.\]
Cách giải:
Ta có: \[ - 1 \le \cos x \le 1{\rm{ }}\forall x \in \mathbb{R} \Leftrightarrow - 1 \le {\left( {m - 1} \right)^2} \le 1 \Leftrightarrow {\left( {m - 1} \right)^2} \le 1 \Leftrightarrow - 1 \le m - 1 \le 1 \Leftrightarrow 0 \le m \le 2.\]
Chú ý: Những phương trình luôn đúng ta không giải, nhiều học sinh mắc sai lầm khi giải bất phương trình \[{\left( {m - 1} \right)^2} \ge - 1\] bằng phương pháp bình phương hai vế.
Câu 6:
 Xem đáp án
Xem đáp án
Đáp án B
Phương pháp:
Giải phương trình lượng giác cơ bản: \[\tan x = \tan \alpha \Leftrightarrow x = \alpha + k\pi \left( {k \in \mathbb{Z}} \right).\]
Cách giải:
ĐK: \[\left\{ \begin{array}{l}\cos x \ne 0\\\cos 3x \ne 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}\cos x \ne 0\\4{\cos ^3}x - 3\cos x \ne 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}\cos x \ne 0\\4{\cos ^2}x - 3 \ne 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}\cos x \ne 0\\\cos x \ne \pm \frac{{\sqrt 3 }}{2}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \ne \frac{\pi }{2} + k\pi \\x \ne \pm \frac{\pi }{6} + k2\pi \end{array} \right.\]
\[\tan x = \tan 3x \Leftrightarrow 3x = x + k\pi \Leftrightarrow 2x = k\pi \Leftrightarrow x = \frac{{k\pi }}{2}\left( {k \in \mathbb{Z}} \right).\]
Đối chiếu điều kiện ta có \[x = k\pi \left( {k \in \mathbb{Z}} \right).\]
Chú ý: HS chú ý điều kiện của phương trình để loại nghiệm.
Câu 7:
 Xem đáp án
Xem đáp án
Đáp án D
Phương pháp:
Giải phương trình lượng giác cơ bản: \[\cot x = \cot \alpha \Leftrightarrow x = \alpha + k\pi \left( {k \in \mathbb{Z}} \right).\]
Cách giải:
ĐK: \[\left\{ \begin{array}{l}\sin x \ne 0\\\sin 2x \ne 0\end{array} \right. \Leftrightarrow \sin 2x \ne 0 \Leftrightarrow 2x \ne k\pi \Leftrightarrow x \ne \frac{{k\pi }}{2}\left( {k \in \mathbb{Z}} \right).\]
\[\cot x = \cot 2x \Leftrightarrow 2x = x + k\pi \Leftrightarrow x = k\pi \left( {k \in \mathbb{Z}} \right)\left( {ktm} \right).\]
Vậy phương trình đã cho vô nghiệm.
Câu 8:
 Xem đáp án
Xem đáp án
Đáp án D
Phương pháp:
Hàm số \[y = \tan x\] tuần hoàn với chu kỳ \[\pi ,\] hàm số \[y = \tan kx\] tuần hoàn với chu kỳ \[\frac{\pi }{k}.\]
Cách giải:
Hàm số \[y = f\left( x \right) = \tan \frac{x}{4}\] tuần hoàn với chu kỳ \[T = \frac{\pi }{{\frac{1}{4}}} = 4\pi .\]
Chú ý: Tránh nhầm lẫn hàm số \[y = \tan kx\] có chu kỳ tuần hoàn là \[T = k\pi .\]
Câu 9:
 Xem đáp án
Xem đáp án
Đáp án B
Phương pháp:
Tổ hợp chập k của n phần tử là số cách lấy ra k phần tử từ tập hợp gồm n phần tử.
Cách giải:
Lớp học có tất cả \[20 + 24 = 44\] học sinh, do đó có \[C_{44}^1 = 44\] cách chọn 1 học sinh làm trực nhật.
Câu 10:
 Xem đáp án
Xem đáp án
Đáp án A
Phương pháp:
+) Chọn 3 người trong số 6 người để trao huy chương.
+) Hoán đổi vị trí của 3 người nhận huy chương.
Cách giải:
Số cách trao một bộ huy chương gồm 1 huy chương vàng, 1 huy chương bạc và 1 huy chương đồng là \[A_6^3 = 120\] cách.
Chú ý: Vị trí của 3 nhận huy chương có thể hoán đổi cho nhau, hay nói cách khác vai trò của 3 huy chương khác nhau nên bài toán này phải dùng chỉnh hợp, dùng tổ hợp là sai.
Câu 11:
 Xem đáp án
Xem đáp án
Đáp án A
Phương pháp:
Gọi số tự nhiên có 6 chữ số là \[\overline {{a_1}{a_2}{a_3}{a_4}{a_5}{a_6}} \left( {0 \le {a_i} \le 9;{a_i} \in \mathbb{N}\left( {i = \overline {1;6} } \right);{a_1} \ne 0} \right)\]
+) Chọn \[{a_6}\] là số lẻ.
+) Sử dụng chỉnh hợp chọn \[{a_1}{a_2}{a_3}{a_4}{a_5}\] trong 7 chữ số còn lại (khác \[{a_6}\]).
+) Sử dụng quy tắc nhân.
Cách giải:
Gọi số tự nhiên có 6 chữ số là \[\overline {{a_1}{a_2}{a_3}{a_4}{a_5}{a_6}} \left( {0 \le {a_i} \le 9;{a_i} \in \mathbb{N}\left( {i = \overline {1;6} } \right);{a_1} \ne 0} \right)\]
Do số tự nhiên cần tìm là số lẻ nên \[{a_6} \in \left\{ {1;3;5;7} \right\} \Rightarrow \] có 4 cách chọn \[{a_6}\]
Số cách chọn \[{a_1}{a_2}{a_3}{a_4}{a_5}\] là \[A_7^5 = 2520\] cách.
Áp dụng quy tắc nhân ta có \[2520.4 = 10080\] số tự nhiên lẻ có 6 chữ số khác nhau được tạo thành.
Câu 12:
 Xem đáp án
Xem đáp án
Đáp án C
Phương pháp:
Số đường chéo của đa giác đều là số đoạn nối 2 đỉnh bất kỳ không kề nhau của đa giác.
Cách giải:
Giả sử đa giác đều n cạnh, khi đó số đường chéo của đa giác đều là \[C_n^2 - n.\]
Vì đa giác đều có 20 đường chéo nên ta có \[C_n^2 - n = 20\]
\[ \Leftrightarrow \frac{{n!}}{{2!\left( {n - 2} \right)!}} - n = 20 \Leftrightarrow \frac{{n\left( {n - 1} \right)}}{2} - n = 20\]
\[ \Leftrightarrow {n^2} - n - 2n = 40 \Leftrightarrow {n^2} - 3n - 40 = 0 \Rightarrow n = 8\]
Vậy đa giác đều đó là bát giác đều.
Chú ý: Các em có thể sử dụng công thức giải nhanh: số đường chéo của đa giác đều n cạnh là \[\frac{{{n^2} - 3n}}{2}.\]
Câu 13:
 Xem đáp án
Xem đáp án
Đáp án B
Phương pháp:
Sử dụng khai triển nhị thức Newton \[{\left( {a + b} \right)^n} = \sum\limits_{k = 0}^n {C_n^k{a^k}{b^{n - k}}.} \]
Cách giải:
Ta có: \[{\left( {x + 1} \right)^6} = \sum\limits_{k = 0}^6 {C_6^k{x^k}.} \]
\[{a_4}\] là hệ số của \[{x^4},\] ứng với \[k = 4.\] Khi đó ta có \[{a_4} = C_6^4 = 15.\]Câu 14:
 Xem đáp án
Xem đáp án
Đáp án C
Phương pháp:
Sử dụng khai triển nhị thức Newton \[{\left( {a + b} \right)^n} = \sum\limits_{k = 0}^n {C_n^k{a^k}{b^{n - k}}.} \]
Cách giải:
Ta có: \[f\left( x \right) = {\left( {{x^2} + \frac{2}{x}} \right)^9} = \sum\limits_{k = 0}^9 {C_9^k{{\left( {{x^2}} \right)}^{9 - k}}{{\left( {\frac{2}{x}} \right)}^k} = \sum\limits_{k = 0}^9 {C_9^k{2^k}{x^{18 - 3k}}.} } \]
Số hạng tự do (số hạng không chứa x) ứng với \[18 - 3k = 0 \Leftrightarrow k = 6.\]
Vậy số hạng tự do trong khai triển trên là \[C_9^6{.2^6} = 5376.\]
Câu 15:
 Xem đáp án
Xem đáp án
Đáp án B
Phương pháp:
Sử dụng khai triển nhị thức Newton \[{\left( {a + b} \right)^n} = \sum\limits_{k = 0}^n {C_n^k{a^k}{b^{n - k}}.} \] sau đó cho \[x = 1\] để tìm tổng các hệ số.
Cách giải:
\[{\left( {2x - 3} \right)^{16}} = \sum\limits_{k = 0}^{16} {C_{16}^k{{\left( {2x} \right)}^k}{{\left( { - 3} \right)}^{16 - k}} = \sum\limits_{k = 0}^{16} {C_{16}^k{2^k}{{\left( { - 3} \right)}^{16 - k}}.{x^k}} } \]
Khi \[x = 1\] ta có \[{\left( {2.1 - 3} \right)^{16}} = \sum\limits_{k = 0}^{16} {C_{16}^k{2^k}{{\left( { - 3} \right)}^{16 - k}}} = 1.\]
Vậy tổng tất cả hệ số trong khai triển trên là 1.
Câu 16:
 Xem đáp án
Xem đáp án
Đáp án C
Phương pháp:
+) Tính số phần tử của không gian mẫu.
+) Tính số phần tử của biến cố.
+) Tính xác suất của biến cố.
Cách giải:
Số cách chọn 2 học sinh bất kì là \[C_{44}^2 = 946\] cách \[ \Rightarrow n\left( \Omega \right) = 946.\]
Gọi A là biến cố: “đội trực nhật có 1 học sinh nam và 1 học sinh nữ”.
Số cách chọn 1 học sinh nam là \[C_{20}^1 = 20\] cách.
Số cách chọn 1 học sinh nữ là \[C_{24}^1 = 24\] cách.
Áp dụng quy tắc nhân ta có \[n\left( A \right) = 20.24 = 480\] cách.
Vậy \[P\left( A \right) = \frac{{480}}{{946}} = \frac{{240}}{{473}}.\]
Câu 17:
 Xem đáp án
Xem đáp án
Đáp án C
Phương pháp:
Số nguyên tố là số chỉ có ước là 1 và chính nó. Số nguyên tố nhỏ nhất là số 2.
Cách giải:
Ta có \[n\left( \Omega \right) = {6^3} = 216.\]
Tích số chấm xuất hiện trên mặt của 3 con súc sắc lập thành một số nguyên tố khi và chỉ khi tích đó là 2, 3 hoặc 5.
TH1: Tích bằng 2, ta có \[2 = 1.1.2 = 1.2.1 = 2.1.1 \Rightarrow \] có 3 cách.
TH2: Tích bằng 3, tương tự có 3 cách.
TH3: Tích bằng 5, tương tự có 3 cách.
Gọi A là biến cố: “Tích số chấm xuất hiện trên mặt của 3 con súc sắc lập thành một số nguyên tố”
\[ \Rightarrow n\left( A \right) = 9.\] Vậy \[P\left( A \right) = \frac{9}{{216}} = \frac{1}{{24}}.\]
Câu 18:
Cho hai điểm \[A\left( {1;2} \right);{\rm{ }}I\left( {3;4} \right).\] Gọi \[A' = {D_I}\left( A \right)\] khi đó điểm \[A'\] có tọa độ là
 Xem đáp án
Xem đáp án
Đáp án B
Phương pháp:
\[A' = {D_I}\left( A \right) \Rightarrow \] I là trung điểm của \[AA'\]
Cách giải:
\[A' = {D_I}\left( A \right) \Rightarrow \] I là trung điểm của \[AA' \Rightarrow A'\left( {5;6} \right).\]
Chú ý: I là trung điểm của \[AA'\]\[ \Rightarrow A' = 2I - A.\]
Câu 19:
 Xem đáp án
Xem đáp án
Đáp án C
Phương pháp:
\[A' = {T_{\overrightarrow u }}\left( A \right) \Rightarrow \overrightarrow {AA'} = \overrightarrow u .\]
Cách giải:
Ta có: \[A' = {T_{\overrightarrow u }}\left( A \right) \Rightarrow \overrightarrow {AA'} = \overrightarrow u \Rightarrow A'\left( {4;6} \right).\]
Câu 20:
 Xem đáp án
Xem đáp án
Đáp án A
Phương pháp:
\[{V_{\left( {I;k} \right)}}\left( A \right) = A' \Leftrightarrow \overrightarrow {IA'} = k\overrightarrow {IA} .\]
Cách giải:
\[{V_{\left( {I;2} \right)}}\left( A \right) = A'\left( {x;y} \right) \Leftrightarrow \overrightarrow {IA'} = 2\overrightarrow {IA} \Leftrightarrow \left\{ \begin{array}{l}x - 3 = 2\left( {1 - 3} \right)\\y - 4 = 2\left( {2 - 4} \right)\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = - 1\\y = 0\end{array} \right. \Rightarrow A'\left( { - 1;0} \right).\]
Câu 21:
 Xem đáp án
Xem đáp án
Đáp án C
Phương pháp:
Ảnh của điểm \[M\left( {x;y} \right)\] qua phép đối xứng trục Ox là \[M'\left( {x; - y} \right).\]
Cách giải:
Ảnh của điểm \[A\left( {1;12} \right)\] qua phép đối xứng trục Ox là \[A'\left( {1; - 12} \right).\]
Câu 22:
 Xem đáp án
Xem đáp án
Đáp án C
Phương pháp:
+) Do \[A'\] đối xứng A qua \[\left( \Delta \right)\] nên đường thẳng \[\left( \Delta \right)\] là đường trung trực của \[AA'.\] Từ đó xác định điểm đi qua và 1VTPT của đường thẳng \[\left( \Delta \right).\]
+) Đường thẳng đi qua \[M\left( {{x_0};{y_0}} \right)\] và có 1 VTPT \[\overrightarrow n = \left( {a;b} \right)\] có phương trình \[a\left( {x - {x_0}} \right) + b\left( {y - {y_0}} \right) = 0.\]
Cách giải:
Do \[A'\] đối xứng A qua \[\left( \Delta \right)\] nên đường thẳng \[\left( \Delta \right)\] là đường trung trực của \[AA'.\] Do đó \[\left( \Delta \right)\] đi qua trung điểm \[I\left( {2;3} \right)\] của \[AA'\] và nhận \[\overrightarrow {AA'} = \left( {2;2} \right)\] là 1 VTPT.
Khi đó ta có phương trình \[\left( \Delta \right):2\left( {x - 2} \right) + 2\left( {y - 3} \right) = 0 \Leftrightarrow x + y - 5 = 0.\]
Câu 23:
 Xem đáp án
Xem đáp án
Đáp án D
Cách giải:
Tập hợp các điểm I là đường thẳng song song với \[\left( \Delta \right)\] và \[\left( {\Delta '} \right)\] và nằm chính giữa \[\left( \Delta \right)\] và \[\left( {\Delta '} \right).\] Do đó có vô số điểm I như vậy.
Câu 24:
 Xem đáp án
Xem đáp án
Đáp án B
Cách giải:
Có duy nhất 1 đường thẳng \[\left( d \right)\] thỏa mãn điều kiện phép đối xứng trục \[\left( d \right)\] biến \[\left( \Delta \right)\] thành \[\left( {\Delta '} \right)\] là \[\left( d \right):x - y - 2 = 0.\]
Câu 25:
 Xem đáp án
Xem đáp án
Đáp án C
Phương pháp:
Phép tịnh tiến theo vectơ \[\overrightarrow u \] biến đường thẳng \[\left( \Delta \right)\] thành chính nó khi và chỉ khi \[\overrightarrow u \] là 1 VTCP của đường thẳng \[\left( \Delta \right).\]
Cách giải:
Dễ thấy đường thẳng \[\left( \Delta \right)\] có 1 VTCP là \[\overrightarrow v = \left( {1;1} \right).\]
Phép tịnh tiến theo vectơ \[\overrightarrow u \] biến đường thẳng \[\left( \Delta \right)\] thành chính nó khi và chỉ khi \[\overrightarrow u \] là 1 VTCP của đường thẳng \[\left( \Delta \right).\]
Khi đó ta có \[\overrightarrow u \] và \[\overrightarrow v \] cùng phương
\[ \Rightarrow \frac{{2017}}{1} = \frac{{{m^2} - 2m - 2017}}{1} \Leftrightarrow {m^2} - 2m - 2017 = 2017 \Leftrightarrow {m^2} - 2m - 4034 = 0\]
Phương trình trên có \[ac < 0 \Rightarrow \] phương trình có 2 nghiệm phân biệt.
Vậy có 2 giá trị của m thỏa mãn yêu cầu bài toán.
Câu 26:
Giải các phương trình lượng giác sau:
1) \[{\sin ^2}x + 5\sin x\cos x + 6{\cos ^2}x = 6\]
 Xem đáp án
Xem đáp án
Phương pháp:
1) TH1: \[\cos x = 0.\]
TH2: \[\cos x \ne 0,\] chia cả 2 vế của phương trình cho \[{\cos ^2}x,\] sử dụng công thức \[\frac{1}{{{{\cos }^2}x}} = 1 + {\tan ^2}x,\] đưa về phương trình bậc hai ẩn \[\tan x.\]
Cách giải:
1) \[{\sin ^2}x + 5\sin x\cos x + 6{\cos ^2}x = 6\]
TH1: \[\cos x = 0 \Leftrightarrow {\sin ^2}x = 1,\] khi đó phương trình trở thành \[1 = 6\] (vô nghiệm).
TH2: \[\cos x \ne 0.\] Chia cả 2 vế của phương trình cho \[{\cos ^2}x,\] ta được:
\[{\tan ^2}x + 5\tan x + 6 = 6\left( {1 + {{\tan }^2}x} \right) \Leftrightarrow 5{\tan ^2}x - 5\tan x = 0\]
\[ \Leftrightarrow 5\tan x\left( {\tan x - 1} \right) = 0 \Leftrightarrow \left[ \begin{array}{l}\tan x = 0\\\tan x = 1\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = k\pi \\x = \frac{\pi }{4} + k\pi \end{array} \right.\left( {k \in \mathbb{Z}} \right)\]
Vậy nghiệm của hệ phương trình là \[S = \left\{ {k\pi ;\frac{\pi }{4} + k\pi |k \in \mathbb{Z}} \right\}.\]
Câu 27:
2) \[\sqrt 3 \sin + \cos x = 2\]
 Xem đáp án
Xem đáp án
Phương pháp:
2) Phương trình dạng \[a\sin x + b\cos x = c,\] chia cả 2 vế của phương trình cho \[\sqrt {{a^2} + {b^2}} .\]
Cách giải:2) \[\sqrt 3 \sin x + \cos x = 2\]
\[ \Leftrightarrow \frac{{\sqrt 3 }}{2}\sin x + \frac{1}{2}\cos x = 1 \Leftrightarrow \sin x\cos \frac{\pi }{6} + \cos x\sin \frac{\pi }{6} = 1\]
\[ \Leftrightarrow \sin \left( {x + \frac{\pi }{6}} \right) = 1 \Leftrightarrow x + \frac{\pi }{6} = \frac{\pi }{2} + k2\pi \Leftrightarrow x = \frac{\pi }{3} + k2\pi \left( {k \in \mathbb{Z}} \right)\]
Vậy tập nghiệm của hệ phương trình là \[S = \left\{ {\frac{\pi }{3} + k2\pi |k \in \mathbb{Z}} \right\}.\]
Câu 28:
 Xem đáp án
Xem đáp án
Phương pháp:
3) Sử dụng công thức biến đổi tổng thành tích \[\cos a - \cos b = - 2\sin \frac{{a + b}}{2}\sin \frac{{a - b}}{2}.\]
Cách giải:
c) \[\cos 3x - \sin 2x - \cos x = 0\]
\[ \Leftrightarrow - 2\sin 2x\sin x - \sin 2x = 0 \Leftrightarrow - \sin 2x\left( {2\sin x + 1} \right) = 0\]
\[ \Leftrightarrow \left[ \begin{array}{l}\sin 2x = 0\\\sin x = - \frac{1}{2}\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}2x = k\pi \\x = \frac{{ - \pi }}{6} + k2\pi \\x = \frac{{7\pi }}{6} + k2\pi \end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = \frac{{k\pi }}{2}\\x = \frac{{ - \pi }}{6} + k2\pi \\x = \frac{{7\pi }}{6} + k2\pi \end{array} \right.{\rm{ }}\left( {k \in \mathbb{Z}} \right)\]
Vậy tập nghiệm của hệ phương trình là \[S = \left\{ {\frac{{k\pi }}{2};\frac{{ - \pi }}{6} + k2\pi ;\frac{{7\pi }}{6} + k2\pi |k \in \mathbb{Z}} \right\}.\]
Câu 29:
 Xem đáp án
Xem đáp án
Phương pháp:
Gọi số tự nhiên có 6 chữ số là \[\overline {{a_1}{a_2}{a_3}{a_4}{a_5}{a_6}} \left( {{a_i} \in \left\{ {0;1;2;3;4;5;6;7} \right\};{a_1} \ne 0} \right).\] Xét các trường hợp sau:
TH1: \[{a_1} = 5;{a_2} \ge 4,{a_2} \ne 5.\]
TH2: \[{a_1} > 5.\]
Cách giải:
Gọi số tự nhiên có 6 chữ số là \[\overline {{a_1}{a_2}{a_3}{a_4}{a_5}{a_6}} \left( {{a_i} \in \left\{ {0;1;2;3;4;5;6;7} \right\};{a_1} \ne 0} \right).\]
TH1: \[{a_1} = 5;{a_2} \ge 4,{a_2} \ne 5 \Rightarrow \] có 3 cách chọn \[{a_2}\] và có \[A_6^4\] cách chọn 4 chữ số còn lại \[ \Rightarrow \] có \[3A_6^4\] số.
TH2: \[{a_1} > 5 \Rightarrow \] có 2 cách chọn \[{a_1}\] và \[A_7^5\] cách chọn 5 chữ số còn lại \[ \Rightarrow \] có \[2A_7^5\] số.
Vậy có tất cả \[3A_6^4 + 2A_7^5 = 6120\] số thỏa mãn.
Câu 30:
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M, N lần lượt là trung điểm của SA, SB, P là trọng tâm của tam giác BCD.
1) Chứng minh rằng: Đường thẳng MN song song với mặt phẳng \[\left( {{\rm{SCD}}} \right){\rm{.}}\]
2) Tìm giao tuyến của \[{\rm{mp}}\left( {{\rm{MNP}}} \right)\] và \[{\rm{mp}}\left( {{\rm{ABCD}}} \right){\rm{.}}\]
3) Tìm giao điểm G của đường thẳng SC và \[{\rm{mp}}\left( {{\rm{MNP}}} \right){\rm{.}}\] Tính tỷ số \[\frac{{SC}}{{SG}}.\]
 Xem đáp án
Xem đáp án
Phương pháp:
1) Chứng minh đường thẳng MN song song với 1 đường thẳng nằm trong mặt phẳng \[\left( {SCD} \right).\]
2) Hai mặt phẳng chứa 2 đường thẳng song song thì cắt nhau theo giao tuyến (nếu có) song song với 2 đường thẳng đó.
3) Áp dụng định lí Menelaus trong tam giác SAC: \[\frac{{MS}}{{MA}}.\frac{{PA}}{{PC}}.\frac{{GC}}{{GS}} = 1.\]
Cách giải:
a) Xét tam giác SAB có MN là đường trung bình \[ \Rightarrow MN{\rm{// }}AB\] (Tính chất đường trung bình).
Lại có \[AB{\rm{ // }}CD\] (ABCD là hình bình hành) nên \[MN{\rm{ // }}CD,\] \[CD \subset \left( {SCD} \right) \Rightarrow MN{\rm{ // }}\left( {SCD} \right).\]
b) Ta có \[\left( {MNP} \right)\] và \[\left( {ABCD} \right)\] có điểm P chung.
\[MN \subset \left( {MNP} \right);{\rm{ }}AB \subset \left( {ABCD} \right);{\rm{ }}MN{\rm{ // }}AB \Rightarrow \] Giao tuyến của 2 mặt phẳng \[\left( {MNP} \right)\] và \[\left( {ABCD} \right)\] là đường thẳng qua P và song song với MN, AB.
Trong \[\left( {ABCD} \right)\] kẻ \[EF{\rm{ // }}AB\left( {E \in AD;{\rm{ }}F \in BC} \right),\] khi đó ta có \[\left( {MNP} \right) \cap \left( {ABCD} \right) = EF.\]
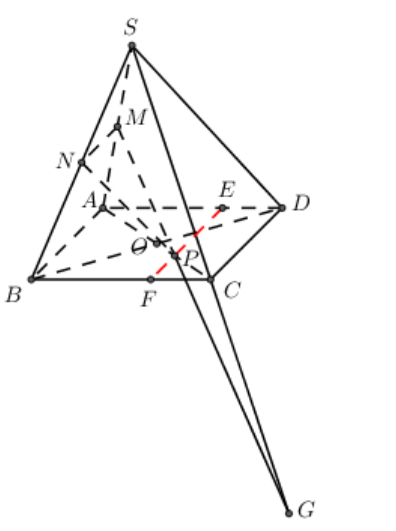
c) Gọi \[O = AC \cap BD.\] Do P là trọng tâm tam giác BCD
\[ \Rightarrow \frac{{PC}}{{PO}} = \frac{2}{3} \Rightarrow \frac{{PC}}{{\frac{1}{2}AC}} = \frac{2}{3} \Leftrightarrow \frac{{PC}}{{AC}} = \frac{1}{3} \Rightarrow \frac{{PC}}{{PA}} = \frac{1}{2}\]
Áp dụng định lí Menelaus trong tam giác SAC: \[\frac{{MS}}{{MA}}.\frac{{PA}}{{PC}}.\frac{{GC}}{{GS}} = 1 \Rightarrow 1.2.\frac{{GC}}{{GS}} = 1 \Leftrightarrow \frac{{GC}}{{GS}} = \frac{1}{2} \Rightarrow \frac{{SC}}{{SG}} = \frac{1}{2}.\]
