Bộ 20 đề thi học kì 1 Toán 11 năm 2022 - 2023 có đáp án
Bộ 20 đề thi học kì 1 Toán 11 năm 2022 - 2023 có đáp án (Đề 5)
-
879 lượt thi
-
24 câu hỏi
-
0 phút
Danh sách câu hỏi
Câu 1:
 Xem đáp án
Xem đáp án
Đáp án D
Phương pháp:
Sử dụng định nghĩa về phép tịnh tiến trong mặt phẳng.
Cách giải:
Gọi \(M\left( {x;y} \right) \in \Delta ;{\rm{ }}{{\rm{T}}_{\overrightarrow n }}\left( M \right) = M'\left( {x';y'} \right) \in \Delta '\)
\( \Rightarrow \left\{ \begin{array}{l}x' = x - 1\\y' = y + 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = x' + 1\\y = y' - 2\end{array} \right. \Rightarrow M\left( {x' + 1;y' - 2} \right) \in {\rm{d}}\)
\(M \in d \Rightarrow 2\left( {x' + 1} \right) - 3\left( {y' - 2} \right) - 5 = 0 \Leftrightarrow 2{\rm{x'}} - 3y' + 3 = 0\)
Vậy phương trình ảnh của đường thẳng Δ là: \(\Delta ' = 2{\rm{x}} - 3y + 3 = 0\).
Câu 2:
 Xem đáp án
Xem đáp án
Đáp án B
Phương pháp:
Sử dụng định nghĩa chỉnh hợp.
Cách giải:
Số cách lấy các số tự nhiên có bốn chữ số khác nhau từ tập X gồm 6 phần tử là: \(A_6^4\).
Câu 3:
 Xem đáp án
Xem đáp án
Đáp án A
Phương pháp:
Khai triển biểu thức, số hạng thứ 6 ứng với \(k = 5\) rồi tìm hệ số.
Cách giải:
Ta có: \({\left( {2{{\rm{x}}^2} + y} \right)^{10}} = \sum\limits_{k = 0}^{10} {C_{10}^k{{\left( {2{{\rm{x}}^2}} \right)}^{10 - k}}{y^k}} \). Số hạng thứ 6 ứng với \(k = 5\)
\( \Rightarrow C_{10}^5{\left( {2{{\rm{x}}^2}} \right)^{10 - 5}}{y^5} = {2^5}C_{10}^5{x^{10}}{y^5} = 8064{{\rm{x}}^{10}}{y^5}\). Hệ số là: 8064.
Câu 4:
 Xem đáp án
Xem đáp án
Đáp án D
Phương pháp:
Giải phương trình tìm nghiệm, kẹp nghiệm trong nửa khoảng đã cho tìm số nghiệm thỏa mãn.
Cách giải:
Ta có: \(\cos 2x = \frac{1}{2} \Leftrightarrow \cos 2x = \cos \frac{\pi }{3} \Leftrightarrow \left[ \begin{array}{l}2x = \frac{\pi }{3} + k2\pi \\2x = - \frac{\pi }{3} + k2\pi \end{array} \right. \Leftrightarrow x = \pm \frac{\pi }{6} + k\pi {\rm{ }}\left( {k \in \mathbb{Z}} \right)\).
Trên nửa khoảng \(\left( {0^\circ ;360^\circ } \right]\) tức \(\left( {0;2\pi } \right]\). Ta sẽ có các nghiệm thỏa mãn như sau:
+) \(0 < x = \frac{\pi }{6} + k\pi \le 2\pi \Leftrightarrow - \frac{1}{6} < k \le \frac{{11}}{6}\) mà \(k \in \mathbb{Z} \Rightarrow k \in \left\{ {0;1} \right\}\). Có 2 nghiệm.
+) \(0 < x = - \frac{\pi }{6} + k\pi \le 2\pi \Leftrightarrow \frac{1}{6} < k \le \frac{{13}}{6}\) mà \(k \in \mathbb{Z} \Rightarrow k \in \left\{ {1;2} \right\}\). Có 2 nghiệm.
Vậy có 4 nghiệm thỏa mãn yêu cầu bài toán.
Câu 5:
 Xem đáp án
Xem đáp án
Đáp án D
Phương pháp:
Vẽ hình sau đó sử dụng định lý Ta-lét trong tam giác.
Cách giải:
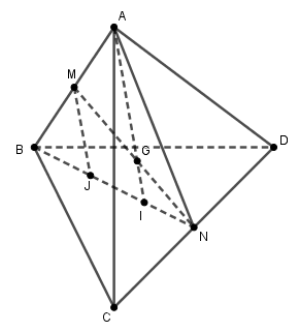
Trong \(\left( {ABN} \right)\) qua M kẻ đường thẳng song song với AI cắt BN tại J.
Xét tam giác MNJ ta có: \(\left\{ \begin{array}{l}GI{\rm{ // MJ}}\\{\rm{GN}} = GM\left( {gt} \right)\end{array} \right. \Rightarrow GI = \frac{1}{2}MJ\) (1).
Xét tam giác BAI ta có: \(\left\{ \begin{array}{l}{\rm{MJ // AI}}\\{\rm{MA}} = MB\end{array} \right. \Rightarrow MJ = \frac{1}{2}AI\) (2).
Từ (1) và (2) \( \Rightarrow GI = \frac{1}{4}AI \Leftrightarrow \frac{{GI}}{{GA}} = \frac{1}{3}\).
Câu 6:
 Xem đáp án
Xem đáp án
Đáp án A
Phương pháp:
Vận dụng các công thức cấp số cộng.
Cách giải:
Ta có: \({u_1} = 3;d = 5;{u_n} = 2018\)
\({u_1} + \left( {n - 1} \right).d = {u_n} \Leftrightarrow 3 + \left( {n - 1} \right).5 = 2018 \Rightarrow n = 404\)
Khi đó tổng số cây ca cao là: \(S = \frac{{n\left( {{u_1} + {u_n}} \right)}}{2} = \frac{{404.\left( {3 + 2018} \right)}}{2} = 408242\).
Câu 7:
 Xem đáp án
Xem đáp án
Đáp án A
Phương pháp:
Áp dụng tính chất của phép quay là bảo toàn độ dài đoạn thẳng.
Cách giải:
Ta có: \(MN = \sqrt {{3^2} + {4^2}} = 5\).
Do phép quay có tính chất bảo toàn độ dài đoạn thẳng nên khi quay một góc \(90^\circ \) thì độ dài đoạn thẳng \(M'N'\) nhận được cũng bằng 5.
Vậy \(M'N' = 5\).
Câu 8:
 Xem đáp án
Xem đáp án
Đáp án A
Phương pháp:
Giải nghiệm phương trình bậc hai tìm nghiệm \(\tan 3{\rm{x}}\) rồi tìm nghiệm x của phương trình.
Cách giải:
Ta có: \({\tan ^2}3{\rm{x}} - \left( {\sqrt 3 - 1} \right)\tan 3{\rm{x}} - \sqrt 3 = 0 \Leftrightarrow \left[ \begin{array}{l}\tan 3{\rm{x}} = - 1\\\tan 3{\rm{x}} = \sqrt 3 \end{array} \right.\)
\( \Leftrightarrow \left[ \begin{array}{l}3{\rm{x}} = - \frac{\pi }{4} + k\pi \\3{\rm{x}} = \frac{\pi }{3} + k\pi \end{array} \right.\left( {k \in \mathbb{Z}} \right) \Leftrightarrow \left[ \begin{array}{l}x = - \frac{\pi }{{12}} + k\frac{\pi }{3}\\x = \frac{\pi }{9} + k\frac{\pi }{3}\end{array} \right.\left( {k \in \mathbb{Z}} \right)\).Câu 9:
 Xem đáp án
Xem đáp án
Đáp án A
Phương pháp:
Tập giá trị của \(\sin \alpha \) luôn thuộc đoạn \(\left[ { - 1;1} \right]\).
Cách giải:
\(\sin 3{\rm{x}} - m = 0 \Leftrightarrow \sin 3{\rm{x}} = m\).
Ta có: \( - 1 \le \sin 3x \le 1 \Rightarrow \) Phương trình có nghiệm \( \Leftrightarrow - 1 \le m \le 1\) hay \(m \in \left[ { - 1;1} \right]\).
Câu 10:
 Xem đáp án
Xem đáp án
Đáp án D
Phương pháp:
Từ biểu thức đã có tìm tọa độ điểm A, rồi tìm ảnh của điểm qua định nghĩa phép vị tự.
Cách giải:
Ta có \(\overrightarrow {OA} = \overrightarrow i - 7\overrightarrow j \Rightarrow \left\{ \begin{array}{l}{x_A} = 1\\{y_A} = - 7\end{array} \right.\).
Nên \({V_{\left( {O; - 3} \right)}}\left( A \right) = A' \Leftrightarrow \overrightarrow {OA'} = - 3\overrightarrow {OA} \Rightarrow A'\left( { - 3;21} \right)\).
Câu 11:
 Xem đáp án
Xem đáp án
Đáp án A
Phương pháp:
Tìm ảnh của tâm I đường tròn, bán kính tăng 2 lần.
Cách giải:
Ta có: Tâm \(A\left( {1; - 2} \right)\), \(R = 3\) của \(\left( C \right)\). Khi đó bán kính mới là: \(R' = 3 \times 2 = 6\)
Lại có: \({V_{\left( {I;2} \right)}}\left( A \right) = A' \Leftrightarrow \overrightarrow {IA'} = 2\overrightarrow {IA} \Rightarrow \left\{ \begin{array}{l}{x_{A'}} - 3 = 2\left( {1 - 3} \right)\\{y_{A'}} - 2 = 2\left( { - 3 - 2} \right)\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x_{A'}} = - 1\\{y_{A'}} = - 8\end{array} \right.\) nên \(A'\left( { - 1; - 8} \right)\).
Vậy ảnh của đường tròn \(\left( C \right)\) là \({\left( {x + 1} \right)^2} + {\left( {y + 8} \right)^2} = 36\).
Câu 12:
 Xem đáp án
Xem đáp án
Đáp án C
Phương pháp:
Tính trực tiếp qua số hạng tổng quát.
Cách giải:
Số hạng thứ 5 ứng với \(n = 5\) nên \({u_5} = \frac{{{{\left( { - 1} \right)}^{5 + 1}}}}{{{2^5}}} = \frac{1}{{32}}\).
Câu 13:
 Xem đáp án
Xem đáp án
Đáp án D
Phương pháp:
Tìm tam giác phù hợp với các điều kiện sau đến lần lượt các điều kiện trước.
Cách giải:
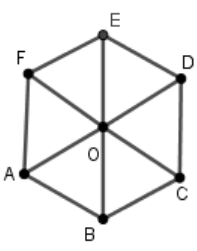
Muốn thu được ảnh là tam giác OBC qua phép quay vị tự tâm O, tỉ số \( - 1\) thì tam giác thực hiện phải là tam giác OEF.
Muốn thu được ảnh là tam giác OEF thông qua phép quay tâm O, góc quay \(120^\circ \) thì tam giác quay phải là tam giác OCD.
Câu 14:
Tìm số hạng không chứa x trong khai triển của biểu thức \({\left( {{x^2} - \frac{2}{{{x^2}}}} \right)^n}\) biết
\(3C_n^1 + {3^2}C_n^2 + {3^3}C_n^3 + ... + {3^n}C_n^{n - 1} + {3^n}C_n^n = 65535\) với \(n \in {\mathbb{N}^*},x \ne 0\).
 Xem đáp án
Xem đáp án
Đáp án A
Phương pháp:
+) Tìm n thông qua dữ kiện đề bài cho.
+) Tìm hệ số không chứa x dựa vào khai triển nhị thức Newton.
Cách giải:
Ta có: \(3C_n^1 + {3^2}C_n^2 + {3^3}C_n^3 + ... + {3^n}C_n^{n - 1} + {3^n}C_n^n = 65535\)
\( \Leftrightarrow {3^0}C_n^0 + 3C_n^1 + {3^2}C_n^2 + {3^3}C_n^3 + ... + {3^n}C_n^{n - 1} + {3^n}C_n^n = 65535 + {3^0}C_n^0\)
\( \Leftrightarrow {\left( {3 + 1} \right)^n} = 65535 \Leftrightarrow {4^n} = 65535 \Leftrightarrow n = 8\).
Khai triển với \(n = 8\) ta được:
\({\left( {{x^2} - \frac{2}{{{x^2}}}} \right)^8} = \sum\limits_{k = 0}^8 {C_8^k{{\left( {{x^2}} \right)}^{8 - k}}.{{\left( { - 2} \right)}^k}.{{\left( {{x^{ - 2}}} \right)}^k}} = \sum\limits_{k = 0}^8 {{{\left( { - 2} \right)}^k}.C_8^k.{x^{16 - 4k}}} \)
Khi đó số hạng không chứa x ứng với:
\(16 - 4k = 0 \Leftrightarrow k = 4\), nên hệ số là: \({\left( { - 2} \right)^4}.C_8^4 = 1120\).
Câu 15:
 Xem đáp án
Xem đáp án
Đáp án B
Phương pháp:
Tìm phần bù khi câu hỏi có cả đại số và hình học.
Cách giải:
Ta có:
Số cách chọn 5 câu từ 25 câu hỏi có \(C_{25}^5\).
Số cách chọn chỉ có câu hỏi đại số là: \(C_{15}^5\) cách.
Số cách chọn chỉ có câu hỏi hình học là: \(C_{10}^5\) cách.
Vậy số cách chọn 5 câu có cả câu hỏi đại số và hình học là: \(C_{25}^5 - C_{15}^5 - C_{10}^5 = 49875\).
Câu 16:
 Xem đáp án
Xem đáp án
Đáp án C
Phương pháp:
Xác định hai điểm chung của hai mặt phẳng.
Cách giải:
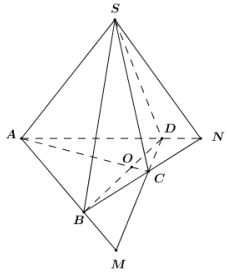
Xét \(\left( {SAB} \right)\) và \(\left( {SC{\rm{D}}} \right)\) có:
+ S là điểm chung thứ nhất.
+ \(M = AB \cap C{\rm{D}} \Rightarrow \left\{ \begin{array}{l}M \in {\rm{A}}B \subset \left( {SAB} \right) \Rightarrow M \in \left( {SAB} \right)\\M \in C{\rm{D}} \subset \left( {SC{\rm{D}}} \right) \Rightarrow M \in \left( {SC{\rm{D}}} \right)\end{array} \right.\)
\( \Rightarrow M \in \left( {SAB} \right) \cap \left( {SC{\rm{D}}} \right) \Rightarrow \) M là điểm chung thứ hai.
Vậy \(\left( {SAB} \right) \cap \left( {SC{\rm{D}}} \right) = SM\).
Câu 17:
 Xem đáp án
Xem đáp án
Đáp án B
Phương pháp:
Phân số xác định khi mẫu số khác 0.
Cách giải:
ĐKXĐ: \(\cos 2x - 1 \ne 0 \Leftrightarrow \cos 2x \ne 1 \Leftrightarrow 2x \ne k2\pi \Leftrightarrow x \ne k\pi {\rm{ }}\left( {k \in \mathbb{Z}} \right)\).
Vậy \(D = \mathbb{R}\backslash \left\{ {k\pi ,k \in \mathbb{Z}} \right\}\).
Câu 18:
 Xem đáp án
Xem đáp án
Đáp án D
Phương pháp:
Chia ra thành 2 tập hợp: Tập hợp A bao gồm các số lẻ, tập hợp B bao gồm các số chẵn.
Chọn ra 6 phần tử từ 2 tập A, B sao cho tổng các phần tử không chia hết cho 2 khi chọn lẻ phần tử của tập A và lẻ phần tử ở tập B thì tổng các phần tử chọn ra là số lẻ nên không chia hết cho 2.
Cách giải:
Không gian mẫu: \(\Omega = C_{13}^6\) cách chọn.
Tập \(A = \left\{ {1;3;5;7;9;11;13} \right\}\) gồm 7 phần tử bao gồm các số lẻ.
Tập \(B = \left\{ {2;4;6;8;10;12} \right\}\) gồm 6 phần tử bao gồm các số chẵn.
Ta có các cách chọn sau:
+) Chọn 5 phần tử tập A và 1 phần tử ở tập B có: \(C_7^5.C_6^1\) cách chọn.
+) Chọn 3 phần tử tập A và 3 phần tử ở tập B có: \(C_7^3.C_6^3\) cách chọn.
+) Chọn 1 phần tử tập A và 5 phần tử ở tập B có: \(C_7^1.C_6^5\) cách chọn.
Xác suất thỏa mãn là: \(\frac{{C_7^5.C_6^1 + C_7^3.C_6^3 + C_7^1.C_6^5}}{{C_{13}^6}} = \frac{{217}}{{429}}\).
Câu 19:
 Xem đáp án
Xem đáp án
Đáp án D
Phương pháp:
Đường thẳng song song với mặt phẳng khi và chỉ khi nó song song với đường thẳng bất kì trong mặt phẳng đó.
Cách giải:
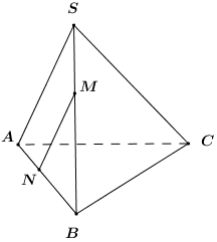
Ta có: \(\frac{{SM}}{{SB}} = \frac{1}{4} \Rightarrow \frac{{BM}}{{B{\rm{S}}}} = \frac{3}{4};NB = 3NA \Rightarrow \frac{{BN}}{{BA}} = \frac{3}{4}\).
Xét tam giác BSA có: \(\frac{{BM}}{{B{\rm{S}}}} = \frac{{BN}}{{BA}} = \frac{3}{4} \Rightarrow MN{\rm{ // SA}}\) nên
\(MN{\rm{ // }}\left( {SAC} \right)\).
Câu 20:
 Xem đáp án
Xem đáp án
Đáp án C
Phương pháp:
Tìm số nghiệm ở phương trình \(\sin x + \cos x = 1\) trong đoạn đã cho, rồi thiết lập điều kiện của m để phương trình \(\sin 4{\rm{x}} = m\) có nghiệm trong đoạn sao cho tổng hai nghiệm cả hai phương trình là bốn nghiệm phân biệt.
Cách giải:
Ta có \(\left( {\sin x + \cos x - 1} \right)\left( {\sin 4x - m} \right) = 0 \Leftrightarrow \left[ \begin{array}{l}\sin x + \cos x = 1{\rm{ }}\left( 1 \right)\\\sin 4x = m{\rm{ }}\left( 2 \right)\end{array} \right.\).
\(\left( 1 \right) \Leftrightarrow \sqrt 2 \sin \left( {x + \frac{\pi }{4}} \right) = 1 \Leftrightarrow \left[ \begin{array}{l}x + \frac{\pi }{4} = \frac{\pi }{4} + k2\pi \\x + \frac{\pi }{4} = \pi - \frac{\pi }{4} + k2\pi \end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = k2\pi \\x = \frac{\pi }{2} + k2\pi \end{array} \right.\left( {k \in \mathbb{Z}} \right)\).
+) \(\frac{\pi }{8} \le x = k2\pi \le \frac{{5\pi }}{6} \Rightarrow \frac{1}{{16}} \le k \le \frac{5}{{12}},k \in \mathbb{Z} \Rightarrow k \in \cancel{\bigcirc }\)
+) \(\frac{\pi }{8} \le x = \frac{\pi }{2} + k2\pi \le \frac{{5\pi }}{6} \Rightarrow - \frac{3}{{16}} \le k \le \frac{1}{6},k \in \mathbb{Z} \Rightarrow k = 0\)
Do đó (1) có nghiệm duy nhất là: \(x = \frac{\pi }{2}\) thỏa mãn yêu cầu.
TH1: \(x = \frac{\pi }{2}\) là 1 nghiệm của (2), khi đó ta có: \(\sin 4\frac{\pi }{2} - m = 0 \Leftrightarrow m = 0\).
Thử lại: Với \(m = 0\) thì \(\sin 4{\rm{x}} = 0 \Leftrightarrow x = \frac{{k\pi }}{4}\left( {k \in \mathbb{Z}} \right)\).
\(\frac{\pi }{8} \le \frac{{k\pi }}{4} \le \frac{{5\pi }}{6} \Leftrightarrow \frac{1}{2} \le k \le \frac{{10}}{3} \Rightarrow k \in \left\{ {1;2;3} \right\} \Rightarrow x \in \left\{ {\frac{\pi }{4};\frac{\pi }{2};\frac{{3\pi }}{4}} \right\}\).
Vậy phương trình ban đầu có 3 nghiệm phân biệt thỏa mãn yêu cầu bài toán \( \Rightarrow m = 0\) loại.
TH2: \(x = \frac{\pi }{2}\) không là nghiệm của (2) \( \Rightarrow m \ne 0\).
Khi đó để phương trình ban đầu có 4 nghiệm thỏa mãn yêu cầu bài toán thì (2) có 3 nghiệm phân biệt thỏa mãn \(x \in \left[ {\frac{\pi }{8};\frac{{5\pi }}{6}} \right]\backslash \left\{ {\frac{\pi }{2}} \right\}\).
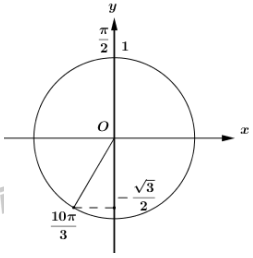
Với \(x \in \left[ {\frac{\pi }{8};\frac{{5\pi }}{6}} \right] \Rightarrow 4{\rm{x}} \in \left[ {\frac{\pi }{2};\frac{{10\pi }}{3}} \right]\), dựa vào đường tròn lượng giác ta tìm được \(m \in \left[ { - \frac{{\sqrt 3 }}{2};1} \right)\).
Vậy \(m \in \left[ { - \frac{{\sqrt 3 }}{2};1} \right)\backslash \left\{ 0 \right\} \Rightarrow \left\{ \begin{array}{l}a = - \frac{{\sqrt 3 }}{2}\\b = 1\\c = 0\end{array} \right. \Rightarrow {a^2} + 2b + c = \frac{3}{4} + 2 = \frac{{11}}{4}\).Câu 21:
 Xem đáp án
Xem đáp án
Cách giải:
Ta có: \(2\sin x = \sqrt 3 \Leftrightarrow \sin x = - \frac{{\sqrt 3 }}{2} \Leftrightarrow \left[ \begin{array}{l}x = - \frac{\pi }{3} + k2\pi \\x = \pi + \frac{\pi }{3} + k2\pi \end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = - \frac{\pi }{3} + k2\pi \\x = \frac{{4\pi }}{3} + k2\pi \end{array} \right.\left( {k \in \mathbb{Z}} \right)\).
Vậy phương trình đã cho có nghiệm: \(x = - \frac{\pi }{3} + k2\pi ;{\rm{ }}x = \frac{{4\pi }}{3} + k2\pi {\rm{ }}\left( {k \in \mathbb{Z}} \right)\).
Câu 22:
a) (0,5 điểm) Đoàn học sinh tham gia Hội thao Giáo dục quốc phòng và an ninh học sinh THPT cấp tỉnh lần thứ V năm 2018 của một trường THPT gồm có 8 học sinh nam và 7 học sinh nữ. Chọn ngẫu nhiên 9 học sinh để tham gia bộ môn thi điều lệnh. Tính xác suất để trong 9 học sinh được chọn ra có đúng 5 học sinh nam.
 Xem đáp án
Xem đáp án
a)
Phương pháp:
+ Tính số phần tử của không gian mẫu.
+ Tính số phần tử của biến cố.
+ Tính xác suất của biến cố.
Cách giải:
Không gian mẫu: \(\Omega = C_{15}^9\) cách chọn.
Số cách chọn đúng 5 học sinh nam trong 8 học sinh nam và 4 học sinh nữ trong 7 học sinh nữ: \(C_8^5.C_7^4\) cách chọn.
Xác suất thỏa mãn là: \(\frac{{C_8^5.C_7^4}}{{C_{15}^9}} = \frac{{56}}{{143}}\).
Câu 23:
 Xem đáp án
Xem đáp án
b)
Phương pháp:
+ Tính số phần tử của không gian mẫu.
+ Tính số phần tử của biến cố.
+ Tính xác suất của biến cố.
Cách giải:
Ta có: \(A_m^2 + 4.C_m^{m - 2} = 60 \Leftrightarrow \frac{{m!}}{{\left( {m - 2} \right)!}} + 4.\frac{{m!}}{{\left( {m - 2} \right)!.2!}} = 60\)
\( \Leftrightarrow 3.\frac{{m!}}{{\left( {m - 2} \right)!}} = 60 \Leftrightarrow m\left( {m - 1} \right) = 20 \Rightarrow m = 5\) (TM).
Lại có: \({\left( {{x^3} - \frac{2}{x}} \right)^{15}} = \sum\limits_{k = 0}^{15} {C_{15}^k{{\left( {{x^3}} \right)}^{15 - k}}{{\left( { - \frac{2}{x}} \right)}^k}} = \sum\limits_{k = 0}^{15} {C_{15}^k.{{\left( { - 2} \right)}^k}{x^{45 - 4k}}} \).
Số hạng chứa \({x^5}\) ứng với: \(45 - 4k = 5 \Leftrightarrow k = 10\).
Vậy số hạng chứa \({x^5}\) là: \(C_{15}^{10}.{\left( { - 2} \right)^{10}}{x^5} = 3075072{{\rm{x}}^5}\).
Câu 24:
Cho hình chóp S.ABCD, đáy ABCD là hình thang có \(A{\rm{D // BC}}{\rm{, AB}} = BC = a\), \(BA{\rm{D}} = 60^\circ \).
a) Gọi M là trung điểm SD. Lấy điểm N nằm trên cạnh SA sao cho \(SN = 2NA\). Tìm giao điểm H của đường thẳng MN và mặt phẳng \(\left( {ABC{\rm{D}}} \right)\).
b) Gọi G là trọng tâm tam giác SAB. Mặt phẳng \(\left( \alpha \right)\) đi qua G và song song với hai đường thẳng AB, CD. Tính chu vi thiết diện của hình chóp S.ABCD cắt bởi mặt phẳng \(\left( \alpha \right)\).
 Xem đáp án
Xem đáp án
Phương pháp:
a) \(\left\{ \begin{array}{l}a \cap b = M\\b \subset \left( P \right)\end{array} \right. \Rightarrow a \cap \left( P \right) = M\).
b) Xác định mặt phẳng \(\left( \alpha \right)\).
Sử dụng định lí Cosin trong tam giác và định lí Ta-lét tính độ dài các cạnh của thiết diện, từ đó tính chu vi thiết diện.
Cách giải:
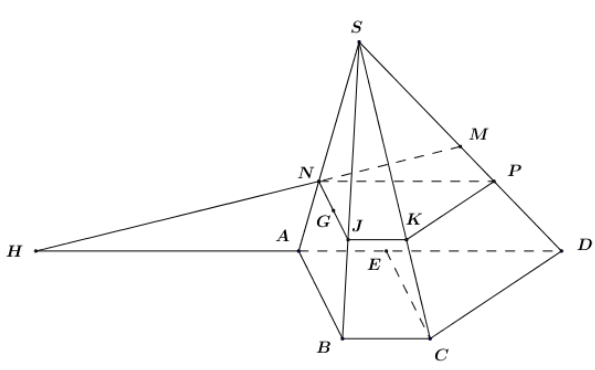
a) Trong mặt phẳng \(\left( {SA{\rm{D}}} \right)\) gọi: \(MN \cap A{\rm{D}} = H\).
Ta có \(\left\{ \begin{array}{l}H \in MN\\H \in {\rm{AD}} \subset \left( {ABC{\rm{D}}} \right) \Rightarrow H \in \left( {ABC{\rm{D}}} \right)\end{array} \right. \Rightarrow H = MN \cap \left( {ABC{\rm{D}}} \right)\).
b) Trong \(\left( {SAB} \right)\) qua G kẻ đường thẳng \(NJ{\rm{ // AB }}\left( {N \in SA,J \in SB} \right)\), ta có:
\(\left\{ \begin{array}{l}G \in \left( \alpha \right) \cap \left( {SAB} \right)\\\left( \alpha \right){\rm{ // AB}} \subset \left( {SAB} \right)\end{array} \right. \Rightarrow \left( \alpha \right) \cap \left( {SAB} \right) = NJ\).
Trong \(\left( {SBC} \right)\) qua J kẻ \(JK{\rm{ // BC }}\left( {K \in SC} \right)\), CMTT ta có \(\left( \alpha \right) \cap \left( {SBC} \right) = JK\).
Trong \(\left( {SA{\rm{D}}} \right)\) qua N kẻ \(NP{\rm{ // AD }}\left( {P \in SD} \right)\), ta có \(\left( \alpha \right) \cap \left( {SA{\rm{D}}} \right) = NP\) và \(\left( \alpha \right) \cap \left( {SBC} \right) = PK\).
Do đó thiết diện của chóp cắt bởi \(\left( \alpha \right)\) là tứ giác NJKP.
Qua C kẻ đường thẳng song song với BA cắt AD tại E.
Dễ dàng chứng minh được ABCE là hình bình hành \( \Rightarrow A{\rm{E}} = BC = a \Rightarrow E{\rm{D}} = AB - A{\rm{E}} = 2{\rm{a}}\).
Lại có \(BA{\rm{D}} = 60^\circ \Rightarrow CE{\rm{D}} = 60^\circ \) (đồng vị).
Xét tam giác CED áp dụng định lý Cosin ta có:
\(C{{\rm{D}}^2} = C{E^2} + D{E^2} - 2CE.DE\cos \left( {CED} \right)\)
\( \Rightarrow C{D^2} = {a^2} + {\left( {2a} \right)^2} - 2 \times a \times 2a \times \cos \left( {60^\circ } \right)\)
\( \Rightarrow C{D^2} = 3{a^2} \Rightarrow CD = a\sqrt 3 \).
Mặt khác: \(\left\{ \begin{array}{l}SN = 2NA \Rightarrow \frac{{SN}}{{SA}} = \frac{2}{3}\\AB{\rm{ // NJ}}{\rm{, BC // JK}}{\rm{, CD // KP}}{\rm{, DA // PN}}\end{array} \right.\)
\( \Rightarrow NJ = \frac{2}{3}AB = \frac{2}{3}a\)
\(JK = \frac{2}{3}BC = \frac{2}{3}a\)
\(NP = \frac{2}{3}A{\rm{D}} = 2{\rm{a}}\)
\(KP = \frac{2}{3}C{\rm{D}} = \frac{{2\sqrt 3 }}{3}a\).
Chu vi thiết diện NJKP bằng: \(NJ + JK + NP + KP = \frac{2}{3}a + \frac{2}{3}a + 2{\rm{a}} + \frac{{2\sqrt 3 }}{3}a = \frac{{10 + 2\sqrt 3 }}{3}a\).
