Đáp án C

Phương pháp:

Áp dụng quy tắc nhân.

Cách giải:

Số cách chọn 1 món ăn: 5 cách.

Số cách chọn 1 loại quả: 5 cách.

Số cách chọn 1 loại đồ uống: 3 cách.

Áp dụng quy tắc nhân ta có số cách chọn thực đơn là 5.5.3 = 75 cách.

Đáp án D

Phương pháp:

Phương trình \[a\sin x + b\cos x = c\]có nghiệm \[ \Leftrightarrow {a^2} + {b^2} \ge {c^2}.\]

Cách giải:

Phương trình \[12\sin x - 5\cos x = m\]có nghiệm \[ \Leftrightarrow {12^2} + {5^2} \ge {m^2} \Leftrightarrow {m^2} \le 169 \Leftrightarrow - 13 \le m \le 13.\]

Vậy có 27 số nguyên m thỏa mãn yêu cầu bài toán

Đáp án A

Phương pháp:

Xác định các điểm chung của hai mặt phẳng.

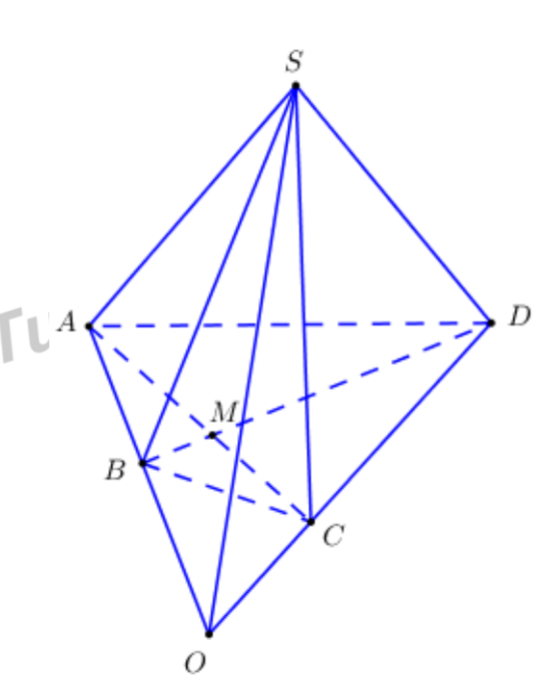
Cách giải:

Ta có\[AB \cap CD = O \Rightarrow \left\{ \begin{array}{l}O \in AB \subset \left( {SAB} \right) \Rightarrow O \in \left( {SAB} \right)\\O \in CD \subset \left( {SCD} \right) \Rightarrow O \in \left( {SCD} \right)\end{array} \right..\]

\[ \Rightarrow O \in \left( {SAB} \right) \cap \left( {SCD} \right)\]

Lại có \[S \in \left( {SAB} \right) \cap \left( {SCD} \right).\]

Vậy \[\left( {SAB} \right) \cap \left( {SCD} \right) = SO.\]

Đáp án A

Phương pháp:

Xét trên đường tròn lượng giác.

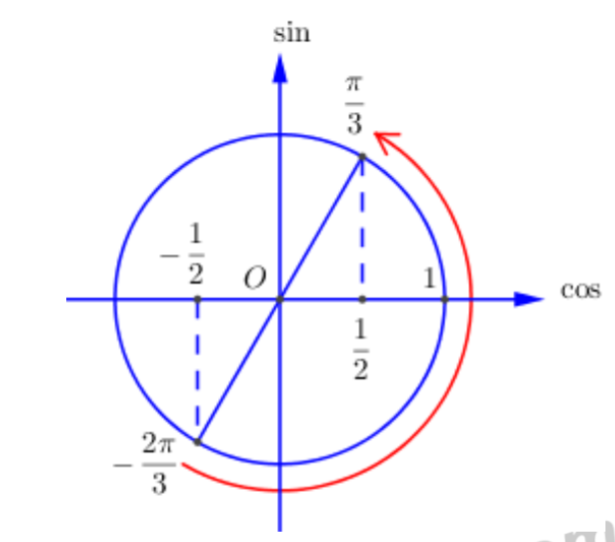
Cách giải:

Ta có\[x \in \left[ { - \frac{\pi }{3};\frac{\pi }{6}} \right] \Rightarrow 2x \in \left[ { - \frac{{2\pi }}{3};\frac{\pi }{3}} \right].\]

Biểu diễn trên đường tròn lượng giác:

Dựa vào đường tròn lượng giác ta thấy với\[2x \in \left[ { - \frac{{2\pi }}{3};\frac{\pi }{3}} \right] \Rightarrow \cos 2x \in \left[ { - \frac{1}{2};1} \right].\]

Vậy\[M = 1;m = - \frac{1}{2} \Rightarrow T = M - 2m = 1 - 2.\left( { - \frac{1}{2}} \right) = 2.\]

Chú ý: Cần biểu diễn trên đường tròn lượng giác, nhiều học sinh nhầm lẫn\[2x \in \left[ { - \frac{{2\pi }}{3};\frac{\pi }{3}} \right] \Rightarrow \cos 2x \in \left[ { - \frac{1}{2};\frac{1}{2}} \right].\]

Đáp án A

Phương pháp:

Hàm số \[y = \tan x\]xác định\[ \Leftrightarrow \cos x \ne 0.\]

Cách giải:

Hàm số \[y = \tan x\]xác định\[ \Leftrightarrow \cos x \ne 0 \Leftrightarrow x \ne \frac{\pi }{2} + k\pi \left( {k \in \mathbb{Z}} \right).\]

Vậy tập xác định\[\mathbb{R}\backslash \left\{ {\frac{\pi }{2} + k\pi \left. {} \right|k \in \mathbb{Z}} \right\}.\]

Đáp án B

Phương pháp:

\[{T_{\overrightarrow u }}\left( M \right) = M' \Leftrightarrow \overrightarrow {MM'} = \overrightarrow u .\]

Cách giải:

Ta có\[\overrightarrow {AA'} = \left( {1; - 2} \right).\]Vì \[{T_{\overrightarrow u }}\left( A \right) = A' \Leftrightarrow \overrightarrow {AA'} = \overrightarrow u = \left( {1; - 2} \right)\], do đó các đáp án C, D sai.

\[{T_{\overrightarrow u }}\left( B \right) = B' \Leftrightarrow \overrightarrow {BB'} = \overrightarrow u \Rightarrow \left\{ \begin{array}{l}{x_{B'}} - 2 = 1\\{y_{B'}} - 3 = - 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x_{B'}} = 3\\{y_{B'}} = 1\end{array} \right. \Rightarrow B'\left( {3;1} \right)\]

\[{T_{\overrightarrow u }}\left( C \right) = C' \Leftrightarrow \overrightarrow {CC'} = \overrightarrow u \Rightarrow \left\{ \begin{array}{l}{x_{C'}} - 6 = 1\\{y_{C'}} - 7 = - 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x_{C'}} = 7\\{y_{C'}} = 5\end{array} \right. \Rightarrow C'\left( {7;5} \right)\]

Vậy đáp án B đúng.

Đáp án B

Phương pháp:

+ Tính số phần tử của không gian mẫu.

+ Tính số phần tử của biến cố.

+ Tính xác suất của biến cố.

Cách giải:

Gieo 1 con súc sắc đồng chất 2 lần \[ \Rightarrow \]Không gian mẫu \[n\left( \Omega \right) = {6^2} = 36.\]

Gọi A là biến cố: “Tích số chấm xuất hiện ở hai lần là một số lẻ”.

\[ \Rightarrow \]Số chấm xuất hiện ở cả 2 lần tung đều là số lẻ.

\[ \Rightarrow n\left( A \right) = 3.3 = 9.\]

Vậy\[P\left( A \right) = \frac{9}{{36}} = \frac{1}{4}.\]

Đáp án D

Phương pháp:

Giải phương trình lượng giác cơ bản \[\cos x = \cos \alpha \Leftrightarrow x = \pm \alpha + 2k\pi \left( {k \in \mathbb{Z}} \right).\]

Cách giải:

\[\cos x = \frac{{\sqrt 2 }}{2} \Leftrightarrow x = \pm \frac{\pi }{4} + k2\pi \left( {k \in \mathbb{Z}} \right).\]

Đáp án B

Phương pháp:

+ \[\sqrt A \]xác định\[ \Leftrightarrow A \ge 0.\]

+ \[\frac{1}{A}\]xác định\[ \Leftrightarrow A \ne 0.\]

Cách giải:

Hàm số \[y = \sqrt {\frac{{1 + \cos x}}{{1 - \sin x}}} \]xác định\[ \Leftrightarrow \left\{ \begin{array}{l}\frac{{1 + \cos x}}{{1 - \sin x}} \ge 0\left( 1 \right)\\1 - \sin x \ne 0\left( 2 \right)\end{array} \right..\]

Ta có: \[\left\{ \begin{array}{l}\cos x \ge - 1\,\,\forall x \Leftrightarrow \cos x + 1 \ge 0\\\sin x \le 1\,\,\forall x \Leftrightarrow 1 - \sin x \ge 0\end{array} \right. \Rightarrow \frac{{\cos x + 1}}{{1 - \sin x}} \ge 0\,\,\forall x\]thỏa mãn (2)

(1)luôn đúng.

Giải (2):\(1 - \sin x \ne 0 \Leftrightarrow \sin x \ne 1 \Leftrightarrow x \ne \frac{\pi }{2} + k2\pi \left( {k \in \mathbb{Z}} \right).\)

Vậy TXĐ\(\mathbb{R}\backslash \left\{ {\frac{\pi }{2} + k2\pi ,k \in \mathbb{Z}} \right\}.\)

Đáp án B

Phương pháp:

+ \(\sqrt A \)xác định\( \Leftrightarrow A \ge 0.\)

+ \(\frac{1}{A}\)xác định\( \Leftrightarrow A \ne 0.\)

Cách giải:

Hàm số \[y = \sqrt {\frac{{1 + \cos x}}{{1 - \sin x}}} \]xác định\[ \Leftrightarrow \left\{ \begin{array}{l}\frac{{1 + \cos x}}{{1 - \sin x}} \ge 0\left( 1 \right)\\1 - \sin x \ne 0\left( 2 \right)\end{array} \right..\]

Ta có: \[\left\{ \begin{array}{l}\cos x \ge - 1\,\,\forall x \Leftrightarrow \cos x + 1 \ge 0\\\sin x \le 1\,\,\forall x \Leftrightarrow 1 - \sin x \ge 0\end{array} \right. \Rightarrow \frac{{\cos x + 1}}{{1 - \sin x}} \ge 0\,\,\forall x\]thỏa mãn (2).

(1) luôn đúng.

Giải (2):\(1 - \sin x \ne 0 \Leftrightarrow \sin x \ne 1 \Leftrightarrow x \ne \frac{\pi }{2} + k2\pi \left( {k \in \mathbb{Z}} \right).\)

Vậy TXĐ \(\mathbb{R}\backslash \left\{ {\frac{\pi }{2} + k2\pi ,k \in \mathbb{Z}} \right\}.\)

Đáp án A

Phương pháp:

Khai triển Newton: \({\left( {a + b} \right)^n} = \sum\limits_{k = 0}^n {C_n^k{a^k}{b^{n - k}}.} \)

Cách giải:

\({\left( {{x^3} - \frac{1}{x}} \right)^{12}} = \sum\limits_{k = 0}^n {C_{12}^k{{\left( {{x^3}} \right)}^{12 - k}}{{\left( { - \frac{1}{x}} \right)}^k} = \sum\limits_{k = 0}^n {C_{12}^k{{\left( { - 1} \right)}^k}{x^{36 - 4k}}.} } \)

Số hạng không chứa x ứng với \(36 - 4k = 0 \Leftrightarrow k = 9.\)

Vậy số hạng không chứa x trong khai triển trên là \(C_{12}^9{\left( { - 1} \right)^9} = - 220.\)

Đáp án A

Phương pháp:

Hàm số \(y = f\left( x \right)\)có tập xác định D được gọi là hàm số chẵn \[ \Leftrightarrow \forall x \in D \Rightarrow - x \in D\]và\[f\left( { - x} \right) = - f\left( x \right).\]

Cách giải:

\[y = \sin \left( {\frac{\pi }{2} - x} \right) = \cos x\]là hàm số chẵn.

Đáp án B

Phương pháp:

Phép đối xứng trục biến đường tròn thành đường tròn có cùng bán kính.

Cách giải:

Đường tròn\[\left( C \right):{\left( {x - 1} \right)^2} + {\left( {y + 2} \right)^2} = 4\] có tâm\[I\left( {1; - 2} \right)\], bán kính\[R = 2\].

Gọi \[I' = {{\rm{\S}}_{Ox}}\left( I \right) \Rightarrow \left\{ \begin{array}{l}{x_{I'}} = {x_I} = 1\\{y_{I'}} = - {y_I} = 2\end{array} \right. \Rightarrow I'\left( {1;2} \right).\]

Vậy ảnh của đường tròn (C) qua phép đối xứng trục Ox là đường tròn \[\left( {C'} \right)\]có tâm\[I'\left( {1;2} \right)\], bán kính \[R = 2\]có phương trình\[{\left( {x - 1} \right)^2} + {\left( {y - 2} \right)^2} = 4.\]

Đáp án B

Phương pháp:

+ Dựng giao tuyến dựa vào các yếu tố song song.

+ Sử dụng định lí Ta-lét.

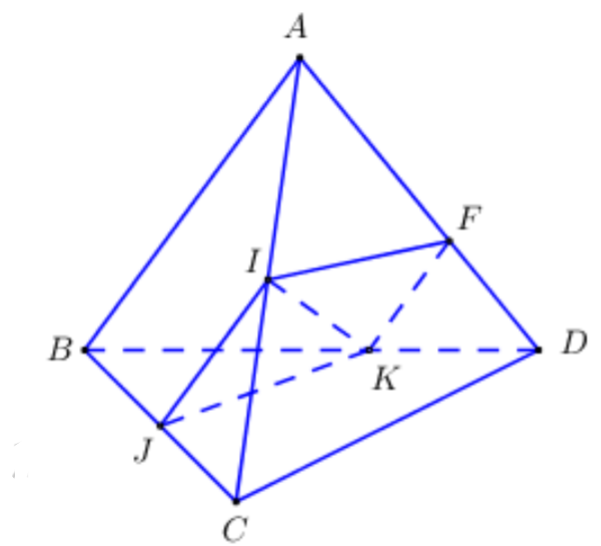
Cách giải:

\[\left\{ \begin{array}{l}\left( {IJK} \right) \supset IJ\\\left( {ABD} \right) \supset AB\\IJ\parallel AB\\K \in \left( {IJK} \right) \cap \left( {ABD} \right)\end{array} \right. \Rightarrow \]Giao tuyến của hai mặt phẳng \[\left( {IJK} \right)\]và \[\left( {ABD} \right)\]là đường thẳng đi qua K và song song với IJ, AB.

Trong \[\left( {ABD} \right)\]kẻ\[KF\parallel AB\left( {F \in AD} \right)\], khi đó ta có\[\left( {IJK} \right) \cap \left( {ABD} \right) = KF \Rightarrow \left( {IJK} \right) \cap AD = F\]

Áp dụng định lí Ta-lét ta có\[\frac{{FA}}{{FD}} = \frac{{KB}}{{KD}} = 2.\]

Đáp án C

Phương pháp:

Dựa vào định nghĩa có tâm đối xứng.

Cách giải:

Hình vuông có 1 tâm đối xứng là tâm hình vuông.

Hình tròn có 1 tâm đối xứng là tâm hình tròn.

Đoạn thẳng có 1 tâm đối xứng là trung điểm của đoạn thẳng.

Đường thẳng là hình có vô số tâm đối xứng.

Đáp án A

Phương pháp:

Sử dụng đường tròn lượng giác.

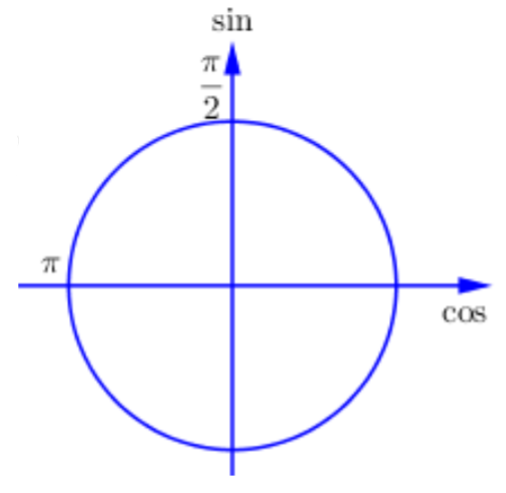
Cách giải:

Quan sát đường tròn lượng giác ta thấy trên khoảng \[\left( {\frac{\pi }{2};\pi } \right)\]hàm số \[y = \cos x\]nghịch biến.

Đáp án A

Phương pháp:

Tam giác được tạo thành từ 3 điểm phân biệt không thẳng hàng.

Cách giải:

TH1: Chọn 2 điểm trong 20 điểm từ đường thẳng thứ nhất có \[C_{20}^2\]cách.

Chọn 1 điểm trong 18 điểm từ đường thẳng thứ hai có \[C_{18}^1 = 18\]cách.

\[ \Rightarrow \]Có \[18.C_{20}^2\]tam giác.

TH2: Chọn 1 điểm trong 20 điểm từ đường thẳng thứ nhất có \[C_{20}^1 = 20\]cách.

Chọn 2 điểm trong 18 điểm từ đường thẳng thứ hai có \[C_{18}^2\]cách.

\[ \Rightarrow \]Có \[20.C_{18}^2\]tam giác.

Vậy có tất cả \[18C_{20}^2 + 20C_{18}^2\]tam giác.

Đáp án D

Phương pháp:

\[{V_{\left( {I;k} \right)}}\left( {\Delta ABC} \right) = \Delta A'B'C' \Rightarrow {S_{\Delta A'B'C'}} = {k^2}.{S_{\Delta ABC}}.\]

Cách giải:

\[{V_{\left( {I;3} \right)}}\left( {\Delta ABC} \right) = \Delta A'B'C' \Rightarrow {S_{\Delta A'B'C'}} = 9.{S_{\Delta ABC}}.\]

Đáp án A

Phương pháp:

- Giải phương trình lượng giác cơ bản:\[\tan x = \tan \alpha \Leftrightarrow x = \alpha + k\pi \left( {k \in \mathbb{Z}} \right).\]

- Tìm các nghiệm thuộc\[\left( {0;3\pi } \right).\]

Cách giải:

\[\tan \left( {2x - \frac{{5\pi }}{6}} \right) + \sqrt 3 = 0 \Leftrightarrow \tan \left( {2x - \frac{{5\pi }}{6}} \right) = - \sqrt 3 \]

\[ \Leftrightarrow 2x - \frac{{5\pi }}{6} = - \frac{\pi }{3} + k\pi \Leftrightarrow 2x = \frac{\pi }{2} + k\pi \Leftrightarrow x = \frac{\pi }{4} + \frac{{k\pi }}{2}\left( {k \in \mathbb{Z}} \right)\]

Xét \[x \in \left( {0;3\pi } \right)\]ta có\[0 < \frac{\pi }{4} + \frac{{k\pi }}{2} < 3\pi \Leftrightarrow 0 < \frac{1}{4} + \frac{k}{2} < 3 \Leftrightarrow - \frac{1}{2} < k < \frac{{11}}{2}.\]

Mà\[k \in \mathbb{Z} \Rightarrow k \in \left\{ {0;1;2;3;4;5} \right\}.\]

Vậy số nghiệm của phương trình thỏa mãn điều kiện là 6.

Đáp án C

Phương pháp:

- Đưa phương trình về dạng tích.

- Giải các phương trình lượng giác cơ bản.

- Tìm nghiệm thuộc khoảng cho trước.

Cách giải:

\[{\cos ^2}x = \sin x\cos x + 2\sin x - \cos x - 2\]

\[ \Leftrightarrow 1 - {\sin ^2}x = \sin x\left( {\cos x + 2} \right) - \left( {\cos x + 2} \right)\]

\[ \Leftrightarrow \left( {1 - \sin x} \right)\left( {1 + \sin x} \right) = \left( {\cos x + 2} \right)\left( {\sin x - 1} \right)\]

\[ \Leftrightarrow \left( {\sin x - 1} \right)\left( {\cos x + 2 + 1 + \sin x} \right) = 0\]

\[ \Leftrightarrow \left( {\sin x - 1} \right)\left( {\sin x + \cos x + 3} \right) = 0\]

\[ \Leftrightarrow \left[ \begin{array}{l}\sin x = 1\\\sin x + \cos x = - 3\left( {\,Vo\,nghiem\,do\,{1^2} + {1^2} < {{\left( { - 3} \right)}^2}} \right)\end{array} \right.\]

\[ \Leftrightarrow x = \frac{\pi }{2} + k2\pi \left( {k \in \mathbb{Z}} \right)\]

Xét\[x \in \left( {\frac{\pi }{2};5\pi } \right)\]ta có \[\frac{\pi }{2} < \frac{\pi }{2} + k2\pi < 5\pi \Leftrightarrow \frac{1}{2} < \frac{1}{2} + 2k < 5 \Leftrightarrow 0 < k < \frac{9}{4}.\]

Mà\[k \in \mathbb{Z} \Rightarrow k \in \left\{ {1;2} \right\} \Rightarrow x \in \left\{ {\frac{{5\pi }}{2};\frac{{9\pi }}{2}} \right\}.\]

Vậy \[T = \frac{{5\pi }}{2} + \frac{{9\pi }}{2} = 7\pi .\]

Đáp án C

Phương pháp:

- Hai góc \[\frac{\pi }{6} - x\]và \[x + \frac{\pi }{3}\]là hai góc phụ nhau.

- Sử dụng công thức nhân đôi\[\cos 2x = 1 - 2{\sin ^2}x.\]

Cách giải:

Ta có:\[\cos 2\left( {x + \frac{\pi }{3}} \right) = 1 - 2{\sin ^2}\left( {x + \frac{\pi }{3}} \right).\]

Lại có\[sin\left( {x + \frac{\pi }{3}} \right) = \cos \left( {\frac{\pi }{2} - x - \frac{\pi }{3}} \right) = \cos \left( {\frac{\pi }{6} - x} \right) \Rightarrow \cos 2\left( {x + \frac{\pi }{3}} \right) = 1 - 2{\cos ^2}\left( {\frac{\pi }{6} - x} \right).\]

Phương trình

\[ \Leftrightarrow 1 - 2{\cos ^2}\left( {\frac{\pi }{6} - x} \right) + 20\cos \left( {\frac{\pi }{6} - x} \right) + 11 = 0\]

\[ \Leftrightarrow - 2{\cos ^2}\left( {\frac{\pi }{6} - x} \right) + 20\cos \left( {\frac{\pi }{6} - x} \right) + 12 = 0\]

\[ \Leftrightarrow - {\cos ^2}\left( {\frac{\pi }{6} - x} \right) + 10\cos \left( {\frac{\pi }{6} - x} \right) + 6 = 0\]

Đặt\[t = \cos \left( {\frac{\pi }{6} - x} \right)\], phương trình đã cho trở thành phương trình\[ - {t^2} + 10t + 6 = 0\]

Đáp án C

Phương pháp:

Sử dụng công thức \[A_n^k = \frac{{n!}}{{\left( {n - k} \right)!}}\]hoặc sử dụng MTCT.

Cách giải:

\[A_7^4 = \frac{{7!}}{{\left( {7 - 4} \right)!}} = \frac{{7!}}{{3!}} = 840.\]

Đáp án A

Phương pháp:

Giải phương trình lượng giác cơ bản\[\sin x = \sin \alpha \Leftrightarrow \left[ \begin{array}{l}x = \alpha + k2\pi \\x = \pi - \alpha + k2\pi \end{array} \right.\left( {k \in \mathbb{Z}} \right).\]

Cách giải:

\[2\sin x - 1 = 0 \Leftrightarrow \sin x = \frac{1}{2} \Leftrightarrow \left[ \begin{array}{l}x = \frac{\pi }{6} + k2\pi \\x = \frac{{5\pi }}{6} + k2\pi \end{array} \right.\left( {k \in \mathbb{Z}} \right).\]

Các điểm biểu diễn hai họ nghiệm trên là điểm C và điểm D.

Đáp án D

Phương pháp:

Sử dụng khai triển nhị thức Newton:\[{\left( {a + b} \right)^n} = \sum\limits_{k = 0}^n {C_n^k{a^k}{b^{n - k}}.} \]

Cách giải:

\[{\left( {1 + 4x} \right)^n} = \sum\limits_{k = 0}^n {C_n^k{{\left( {4x} \right)}^k}{1^{n - k}} = } \sum\limits_{k = 0}^n {C_n^k{4^k}{x^k}} .\]

Hệ số của số hạng chứa \[{x^2}\]trong khai triển trên là\[C_n^2{4^2} = 16C_n^2.\]

Theo bài ra ta có:\[16C_n^2 = 3040 \Leftrightarrow C_n^2 = 190 \Leftrightarrow \frac{{n!}}{{2!\left( {n - 2} \right)!}} = 190.\]

\[ \Leftrightarrow n\left( {n - 1} \right) = 380 \Leftrightarrow {n^2} - n - 380 = 0 \Leftrightarrow \left[ \begin{array}{l}n = 20\,\,\,\left( {tm} \right)\\n = - 19\,\,\,\left( {ktm} \right)\end{array} \right.\]

Vậy\[n = 20.\]

Đáp án D

Phương pháp:

- Tính số phần tử của không gian mẫu.

- Tính số phần tử của biến cố.

- Tính xác suất của biến cố.

Cách giải:

Có tất cả \[15 + 10 + 5 = 30\]câu hỏi.

Chọn 5 câu bất kì trong 30 câu hỏi được 1 đề thi nên số đề thi được tạo ra là\[C_{30}^5.\]

Gọi A là biến cố: “Lấy ra được một đề thi “Tốt””.

TH1: Có 2 câu hỏi ở mức độ khó \[ \Rightarrow \]Có \[C_5^2.C_{15}^1.C_{10}^2 + C_5^2.C_{15}^2.C_{10}^1\]đề.

TH2: Có 3 câu hỏi ở mức độ khó \[ \Rightarrow \]Có \[C_5^3.C_{15}^1.C_{10}^1\]đề.

\[ \Rightarrow n\left( A \right) = C_5^2.C_{15}^1.C_{10}^2 + C_5^2.C_{15}^2.C_{10}^1 + C_5^3.C_{15}^1.C_{10}^1 = 18750\]

\[ \Rightarrow P\left( A \right) = \frac{{18750}}{{C_{30}^5}} = \frac{{3125}}{{23751}}\]

Phương pháp:

Sử dụng khai triển\[{\left( {x + 1} \right)^n}\], thay \[x = 1\]và\[x = - 1.\]

Cách giải:

\[\frac{1}{{1!\left( {n - 1} \right)!}} + \frac{1}{{3!\left( {n - 3} \right)!}} + \frac{1}{{5!\left( {n - 5} \right)!}} + ... + \frac{1}{{\left( {n - 1} \right)!1!}} = \frac{{{2^{n - 1}}}}{{n!}}\]

\[ \Leftrightarrow \frac{{n!}}{{1!\left( {n - 1} \right)!}} + \frac{{n!}}{{3!\left( {n - 3} \right)!}} + \frac{{n!}}{{5!\left( {n - 5} \right)!}} + ... + \frac{{n!}}{{\left( {n - 1} \right)!1!}} = {2^{n - 1}}\]

\[ \Leftrightarrow C_n^1 + C_n^3 + C_n^5 + ... + C_n^{n - 1} = {2^{n - 1}}\]

Xét khai triển\[{\left( {x + 1} \right)^n} = \sum\limits_{k = 0}^n {C_n^k{x^k}.} \]

Thay \[x = 1\]ta có\[{\left( {1 + 1} \right)^n} = \sum\limits_{k = 0}^n {C_n^k} \Leftrightarrow {2^n} = C_n^0 + C_n^1 + C_n^2 + ... + C_n^{n - 1} + C_n^n\,\,\,\left( 1 \right).\]

Thay \[x = - 1\]ta có\[{\left( { - 1 + 1} \right)^n} = \sum\limits_{k = 0}^n {C_n^k} {\left( { - 1} \right)^k} \Leftrightarrow 0 = C_n^0 - C_n^1 + C_n^2 + ... - C_n^{n - 1} + C_n^n\,\,\,\left( 2 \right)\]

Cách giải:

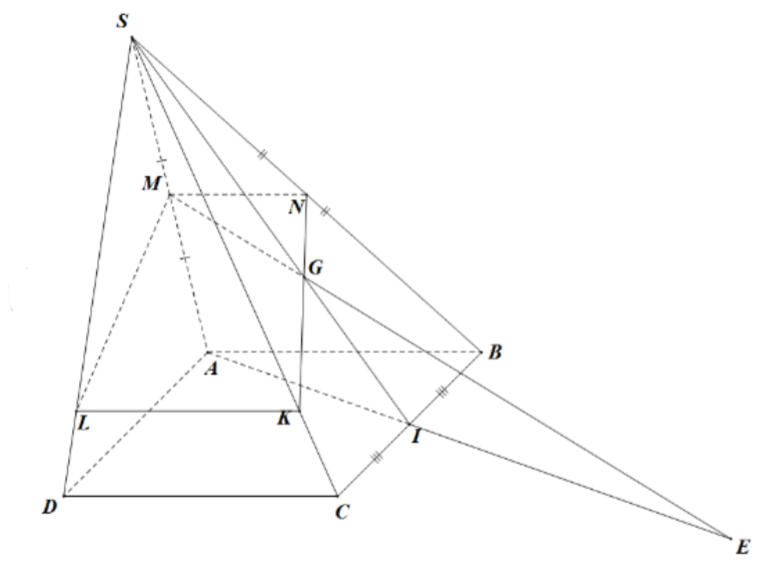
a)   Xét \[\left( {SAI} \right)\]có \[\left\{ \begin{array}{l}\frac{{SM}}{{SA}} = \frac{1}{2}\\\frac{{SG}}{{SI}} = \frac{3}{5}\end{array} \right. \Rightarrow \frac{{SM}}{{SA}} \ne \frac{{SG}}{{SI}} \Rightarrow MG\]không song song với AI.

Gọi \[AI \cap MG = \left\{ E \right\} \Rightarrow \left\{ \begin{array}{l}E \in MG\\E \in AI \subset \left( {ABCD} \right)\end{array} \right. \Rightarrow MG \cap \left( {ABCD} \right) = \left\{ E \right\}.\]

b)  Xét mặt phẳng \[\left( {SBC} \right)\]có: \[\left\{ \begin{array}{l}\frac{{SN}}{{SB}} = \frac{1}{2}\\\frac{{SG}}{{SI}} = \frac{3}{5}\end{array} \right. \Rightarrow \frac{{SN}}{{SB}} \ne \frac{{SG}}{{SI}} \Rightarrow NG\]không song song với BC.

Gọi\[NG \cap SC = \left\{ K \right\} \Rightarrow \left\{ \begin{array}{l}K \in NG \subset \left( {MNG} \right)\\K \in SC \subset \left( {SBC} \right)\end{array} \right..\]

Ta có\[\left( {MNG} \right) \cap \left( {SAB} \right) = MN;\left( {MNG} \right) \cap \left( {SBC} \right) = NK.\]

Xét\[\left( {SAB} \right)\] có \[MN\parallel AB \Rightarrow MN\parallel CD.\]

Ta có \[MN\parallel CD,MN \subset \left( {MNG} \right),CD \subset \left( {SCD} \right)\]và \[K = \left( {SCD} \right) \cap \left( {MNG} \right)\]nên từ K kẻ đường thẳng\[Kx\parallel CD\], gọi\[Kx \cap SD = L.\]

\[ \Rightarrow KL = \left( {SCD} \right) \cap \left( {MNG} \right)\].

Vậy thiết diện của hình chóp S.ABCD cắt bởi mặt phẳng\[\left( {MNG} \right)\]là hình thang\[MNKL\left( {MN\parallel KL} \right)\].