Đáp án C

Phương pháp giải:

Hàm phân thức xác định khi mẫu thức khác 0.

Hàm \[\tan x\] xác định \[ \Leftrightarrow \sin x \ne 0\].

Giải chi tiết:

ĐKXĐ: \[\left\{ {\begin{array}{*{20}{l}}{\tan {\mkern 1mu} x \ne 0}\\{\cos x \ne 0}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{\sin x \ne 0}\\{\cos x \ne 0}\end{array}} \right. \Leftrightarrow \sin 2x \ne 0 \Leftrightarrow 2x \ne k\pi \Leftrightarrow x \ne k\frac{\pi }{2}{\mkern 1mu} {\mkern 1mu} \left( {k \in Z} \right)\]

TXĐ: \[D = R\backslash \left\{ {k\frac{\pi }{2},k \in Z} \right\}\].

Đáp án D

Phương pháp giải:

Sử dụng công thức nhân đôi: \[\cos 2x = 1 - 2{\sin ^2}x\]

Giải chi tiết:

Ta có: \[{\sin ^2}x = 1 \Leftrightarrow \cos 2x = 1 - 2{\sin ^2}x = 1 - 2.1 = - 1\]

Đáp án D

Phương pháp giải:

Biểu diễn các góc lượng giác thuộc khoảng \[\left( { - \frac{{3\pi }}{4};\frac{\pi }{4}} \right)\] trên đường tròn lượng giác, từ đó kết luận tập giá trị của hàm số \[y = \cos x\] trên khoảng đó.

Giải chi tiết:

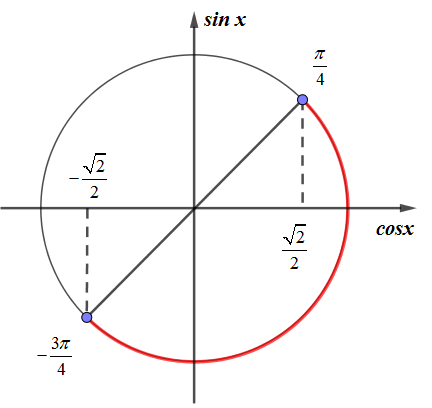
Biểu diễn các góc lượng giác thuộc khoảng \[\left( { - \frac{{3\pi }}{4};\frac{\pi }{4}} \right)\] trên đường tròn lượng giác, ta thấy: tập giá trị của hàm số \[y = \cos x\] trên khoảng đó là: \[\left( { - \frac{{\sqrt 2 }}{2};1} \right]\]

Đáp án D

Phương pháp giải:

\[\sin 2x = 2\sin {\mkern 1mu} x\cos x;{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} \sqrt 2 \sin \left( {x - \frac{\pi }{4}} \right) = \sin x - \cos x\]

Giải chi tiết:

Ta có: \[\sin 2x + \sqrt 2 \sin \left( {x - \frac{\pi }{4}} \right) = 1 \Leftrightarrow 2\sin x\cos x + \left( {\sin {\mkern 1mu} x - \cos x} \right) = 1\] (1)

Đặt \[t = \sin {\mkern 1mu} x - \cos x \Leftrightarrow {t^2} = {\left( {\sin {\mkern 1mu} x - \cos x} \right)^2} \Leftrightarrow {t^2} = 1 - 2\sin x\cos x \Leftrightarrow 2\sin x\cos x = 1 - {t^2}\]

Khi đó, \[\left( 1 \right) \Leftrightarrow 1 - {t^2} + t = 1 \Leftrightarrow {t^2} - t = 0\]

Đáp án D

Phương pháp giải:

Giải chi tiết:

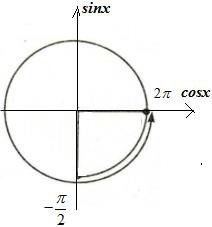
Ta có:

\[{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} 4{\cos ^3}x + 2\cos 2x + 2 = \left( {m + 3} \right)\cos x{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} (*){\mkern 1mu} \]

\[ \Leftrightarrow 4{\cos ^3}x + 4{\cos ^2}x - \left( {m + 3} \right)\cos x = 0\]

\[ \Leftrightarrow \left( {4{{\cos }^2}x + 2\cos x - \left( {m + 3} \right)} \right).\cos x = 0\]

\[ \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{4{{\cos }^2}x + 4\cos x - \left( {m + 3} \right) = 0{\mkern 1mu} {\mkern 1mu} (1)}\\{\cos x = 0{\mkern 1mu} {\mkern 1mu} (2)}\end{array}} \right.\]

Phương trình \[(2) \Leftrightarrow x = \frac{\pi }{2} + k\pi {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} \left( {k \in Z} \right)\]. Mà \[x \in \left( { - \frac{\pi }{2};2\pi } \right] \Rightarrow \left[ {\begin{array}{*{20}{l}}{x = \frac{\pi }{2}}\\{x = \frac{{3\pi }}{2}}\end{array}} \right.\]

Thay \[\cos x = 0\] vào (1): \[{4.0^2} + 4.0 - \left( {m + 3} \right) = 0 \Leftrightarrow m = - 3\]

+) Với \[m = - 3\]:

Phương trình \[(1) \Leftrightarrow 4{\cos ^2}x + 4\cos x = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{\cos x = 0}\\{\cos x = - 1}\end{array}} \right. \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = \frac{\pi }{2} + k\pi }\\{x = \pi + k2\pi }\end{array}} \right.{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} ,k \in \mathbb{Z}\]

Mà \[x \in \left( { - \frac{\pi }{2};2\pi } \right] \Rightarrow x \in \left\{ {\frac{\pi }{2};\frac{{3\pi }}{2};\pi } \right\}\]

Phương trình \[(*)\] có đúng 3 nghiệm thuộc \[\left( { - \frac{\pi }{2};2\pi } \right]\] là \[\left\{ {\frac{\pi }{2};\frac{{3\pi }}{2};\pi } \right\} \Rightarrow m = - 3\] không thỏa mãn

+) Với \[m \ne - 3\]: Phương trình (1) không có nghiệm \[x = \frac{\pi }{2},{\mkern 1mu} {\mkern 1mu} x = \frac{{3\pi }}{2}\]. Khi đó, để (*) có đúng 5 nghiệm thuộc \[\left( { - \frac{\pi }{2};2\pi } \right]\] thì phương trình (1) có đúng 3 nghiệm thuộc \[\left( { - \frac{\pi }{2};2\pi } \right]\]

Đặt \[\cos x = t\], (1) trở thành: \[4{t^2} + 4t - \left( {m + 3} \right) = 0\] (3)

Phương trình (1) có đúng 3 nghiệm thuộc \[\left( { - \frac{\pi }{2};2\pi } \right]\]⇔ Phương trình (3) có 2 nghiệm \[{t_1},{\mkern 1mu} {\mkern 1mu} {t_2}{\mkern 1mu} {\mkern 1mu} \left( {{t_1} \le {t_2}} \right)\] thỏa mãn:

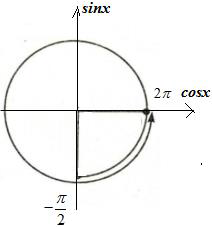
hoặc \[\left\{ {\begin{array}{*{20}{l}}{{t_1} = - 1}\\{{t_2} \in \left( { - 1;0} \right] \cup \left\{ 1 \right\}}\end{array}} \right.\], hoặc \[{t_1} = {t_2} \in \left( {0;1} \right)\], hoặc \[\left\{ {\begin{array}{*{20}{l}}{{t_1} \in \left( {0;1} \right)}\\{{t_2} > 1}\end{array}} \right.\], hoặc \[\left\{ {\begin{array}{*{20}{l}}{{t_1} < - 1}\\{{t_2} \in \left( {0;1} \right)}\end{array}} \right.\]

TH1: \[\left\{ {\begin{array}{*{20}{l}}{{t_1} = - 1}\\{{t_2} \in \left( { - 1;0} \right] \cup \left\{ 1 \right\}}\end{array}} \right.\]

\[ \Rightarrow 4.{\left( { - 1} \right)^2} + 4.\left( { - 1} \right) - \left( {m + 3} \right) = 0 \Leftrightarrow m = - 3\] (loại)

TH2: \[{t_1} = {t_2} \in \left( {0;1} \right)\]

\[ \Rightarrow \Delta ' = 0 \Leftrightarrow 4 + 4\left( {m + 3} \right) \Leftrightarrow 4m + 16 = 0 \Leftrightarrow m = - 4\]

Khi đó, (3) có 2 nghiệm \[{t_1} = {t_2} = - \frac{1}{2} \notin \left( {0;1} \right){\mkern 1mu} {\mkern 1mu} \Rightarrow m = - 4\]: không thỏa mãn

TH3:

\[\left\{ {\begin{array}{*{20}{l}}{{t_1} \in \left( {0;1} \right)}\\{{t_2} > 1}\end{array}} \right. \Leftrightarrow 0 < {t_1} < 1 < {t_2} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{\Delta ' > 0}\\{{t_1}{t_2} > 0}\\{{t_1} + {t_2} > 0}\\{\left( {{t_1} - 1} \right)\left( {{t_2} - 1} \right) < 0}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{\Delta ' > 0}\\{{t_1}{t_2} > 0}\\{{t_1} + {t_2} > 0}\\{{t_1}{t_2} - \left( {{t_1} + {t_2}} \right) + 1 < 0}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{4m + 16 > 0}\\{ - \frac{{m + 3}}{4} > 0}\\{ - \frac{4}{4} > 0}\\{1 - \left( { - \frac{4}{4}} \right) - \frac{{m + 3}}{4} < 0}\end{array}} \right. \Leftrightarrow m \in \emptyset \]

TH4:

\[\left\{ {\begin{array}{*{20}{l}}{{t_1} < - 1}\\{{t_2} \in \left( {0;1} \right)}\end{array}} \right. \Leftrightarrow {t_1} < - 1 < 0 < {t_2} < 1 \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{\Delta ' > 0}\\{{t_1}{t_2} < 0}\\{\left( {{t_1} + 1} \right)\left( {{t_2} + 1} \right) < 0}\\{\left( {{t_1} - 1} \right) + \left( {{t_2} - 1} \right) < 0}\\{\left( {{t_1} - 1} \right)\left( {{t_2} - 1} \right) > 0}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{4m + 16 > 0}\\{ - \frac{{m + 3}}{4} < 0}\\{ - \frac{{m + 3}}{4} + \left( { - \frac{4}{4}} \right) + 1 < 0}\\{ - \frac{4}{4} - 2 < 0}\\{ - \frac{{m + 3}}{4} - \left( { - \frac{4}{4}} \right) + 1 > 0}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{m > - 4}\\{m > - 3}\\{m < 5}\end{array}} \right. \Leftrightarrow m \in \left( { - 3;5} \right)\]

Vậy, tập các giá trị thực của m thỏa mãn yêu cầu đề bài là: \[S = \left( { - 3;5} \right)\]

Đáp án C

Phương pháp giải:

Chia ra 4 trường hợp: 1 chữ số , 2 chữ số đôi một khác nhau, 3 chữ số đôi một khác nhau, 4 chữ số đôi một khác nhau.

Giải chi tiết:

Số các số có thể lập được bao nhiêu số tự nhiên có các chữ số đôi một khác nhau là: \[A_4^1 + A_4^2 + A_4^3 + A_4^4\].

Đáp án B

Phương pháp giải:

Áp dụng quy tắc nhân và quy tắc vách ngăn.

Giải chi tiết:

Xếp 6 học sinh lớp 11 thành 1 hàng có 6! cách

Khi đó, tạo ra 5 vách ngăn 6 học sinh này. Xếp 3 học sinh lớp 12 vào 5 vách ngăn đó (không có học sinh nào vào cùng 1 vách ngăn), có: \[A_5^3\] cách

⇒ Có tất cả \[6!.A_5^3\] cách xếp thỏa mãn.

Đáp án B

Phương pháp giải:

Xác suất của biến cố A: \[P\left( A \right) = \frac{{n\left( A \right)}}{{n\left( \Omega \right)}}\]

Giải chi tiết:

Số phần tử của không gian mẫu: \[n\left( \Omega \right) = C_{52}^8\]

Gọi A : “lấy được 5 quân màu đỏ”

Khi đó \[n\left( A \right) = C_{26}^5.C_{26}^3{\mkern 1mu} {\mkern 1mu} \Rightarrow \] \[P\left( A \right) = \frac{{n\left( A \right)}}{{n\left( \Omega \right)}} = \frac{{C_{26}^5.C_{26}^3}}{{C_{52}^8}}\].

Đáp án B

Phương pháp giải:

Khai triển nhị thức newton: \[{(x + y)^n} = \sum\limits_{i = 0}^n {C_n^i{x^i}.{y^{n - i}}} \]

Giải chi tiết:

Ta có: \[{\left( {{x^2} - 2x} \right)^{10}} = \sum\limits_{i = 0}^{10} {C_{10}^i{{\left( {{x^2}} \right)}^i}.{{\left( { - 2x} \right)}^{10 - i}}} = \sum\limits_{i = 0}^{10} {C_{10}^i{{\left( { - 2} \right)}^{10 - i}}{x^{10 + i}}} \]

Số hạng chứa \[{x^{17}}\] trong khai triển tương ứng với i thỏa mãn: \[10 + i = 17 \Leftrightarrow i = 7\]

Hệ số của số hạng chứa \[{x^{17}}\] trong khai triển là: \[C_{10}^7{\left( { - 2} \right)^{10 - 7}} = - C_{10}^3{.2^3}\].

Đáp án C

Phương pháp giải:

Giải chi tiết:

Ta có:

\[S = {\left( {C_{2017}^0} \right)^2} + {\left( {C_{2017}^1} \right)^2} + {\left( {C_{2017}^2} \right)^2} + ... + {\left( {C_{2017}^{2017}} \right)^2} = C_{2017}^0C_{2017}^{2017} + C_{2017}^1C_{2017}^{2016} + C_{2017}^2C_{2017}^{2015} + ... + C_{2017}^{2017}C_{2017}^0\]

Xét bài toán: Có 4034 viên bi, trong đó có 2017 viên bi xanh, 2017 viên bi đỏ. Tính số cách để lấy được 2017 viên bi từ 4034 viên bi nói trên.

Giải:

Số cách để lấy được 2017 viên bi từ 4034 viên bi nói trên là:

\[C_{4034}^{2017} = C_{2017}^0C_{2017}^{2017} + C_{2017}^1C_{2017}^{2016} + C_{2017}^2C_{2017}^{2015} + ... + C_{2017}^{2017}C_{2017}^0\]

\[ \Rightarrow S = C_{2017}^0C_{2017}^{2017} + C_{2017}^1C_{2017}^{2016} + C_{2017}^2C_{2017}^{2015} + ... + C_{2017}^{2017}C_{2017}^0 = C_{4034}^{2017}\]

Đáp án D

Phương pháp giải:

Giải chi tiết:

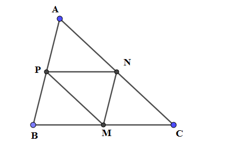
Phát biểu SAI là: Phép tịnh tiến theo vectơ \[\overrightarrow {BP} \] biến tam giác PMN thành tam giác APN.

Đáp án A

Phương pháp giải:

Cho \[d{\rm{//}}d'\], lấy \[A \in d\], \[{T_{\vec v}}:A \mapsto A' \in d'{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} \Rightarrow {T_{\vec v}}:d \mapsto d'\].

Giải chi tiết:

Dễ dàng kiểm tra được \[\left( d \right):2x - y + 1 = 0\] và \[\left( {d'} \right):2x - y + 5 = 0\] song song với nhau.

Lấy \[A\left( {0;1} \right) \in d\], phép tịnh tiến \[{T_{\vec v\left( {a;b} \right)}}:A \mapsto A'{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} \Rightarrow \left\{ {\begin{array}{*{20}{l}}{{x_{A'}} = a}\\{{y_{A'}} = 1 + b}\end{array}} \right.\]

Để phép tịnh tiến theo vectơ \[\vec v\] nào sau đây biến d thành d’ thì

\[A'{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} \in d' \Leftrightarrow 2.a - \left( {1 + b} \right) + 5 = 0 \Leftrightarrow 2a - b + 4 = 0\]

Kiểm tra các đáp án, ta thấy: \[\vec v = \left( {1;6} \right)\] thỏa mãn.

Đáp án A

Phương pháp giải:

\[{V_{\left( {I;k} \right)}}\left( M \right) = M' \Leftrightarrow \overrightarrow {IM'} = k\overrightarrow {IM} \]

Giải chi tiết:

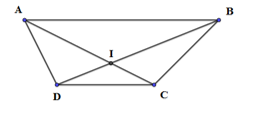
\[\overrightarrow {DC} = \frac{1}{2}\overrightarrow {AB} \Rightarrow \left\{ {\begin{array}{*{20}{l}}{\overrightarrow {IC} = - \frac{1}{2}\overrightarrow {IA} }\\{\overrightarrow {ID} = - \frac{1}{2}\overrightarrow {IB} }\end{array}} \right.{\mkern 1mu} {\mkern 1mu} \Rightarrow {V_{\left( {I;k = - \frac{1}{2}} \right)}}:AB \mapsto CD\]

Đáp án B

Phương pháp giải:

Nếu \[a{\rm{//}}a'\] thì a và a′ đồng phẳng.

Giải chi tiết:

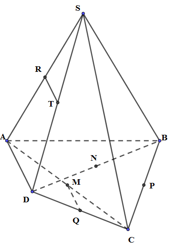
Ta có: \[RT{\rm{//}}AD\] (do \[RT\] là đường trung bình của tam giác \[SAD\])

\[MQ{\rm{//}}AD\] (do \[RT\] là đường trung bình của tam giác \[ACD\])

\[ \Rightarrow RT{\rm{//}}MQ \Rightarrow \] M, Q, R, T đồng phẳng.

Đáp án B

Phương pháp giải:

Giải chi tiết:

Khẳng định SAI là: Nếu d song song với \[\left( \alpha \right)\] và đường thẳng \[d' \subset \left( \alpha \right)\] thì d’ song song với d.

Đáp án D

Phương pháp giải:

Dựa vào các yếu tố song song xác định thiết diện.

Giải chi tiết:

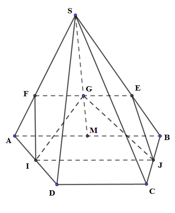
Qua G dựng EF song song AB (\[E \in SB,F \in SA\])

IJ là đường trung bình của hình thang ABCD \[ \Rightarrow \left\{ {\begin{array}{*{20}{l}}{IJ{\rm{//}}AB{\rm{//}}CD}\\{IJ = \frac{{AB + CD}}{2}}\end{array}} \right.\]

Ta có: \[\left\{ {\begin{array}{*{20}{l}}{IJ{\rm{//}}AB}\\{AB{\rm{//}}EF}\end{array}} \right. \Rightarrow IJ{\rm{//}}EF \Rightarrow I,J,E,F\] đồng phẳng

\[ \Rightarrow I,J,E,F,G\] đồng phẳng

\[ \Rightarrow \left( {GIJ} \right) \equiv \left( {IJEF} \right)\]

Thiết diện của \[\left( {GIJ} \right)\] với hình chóp là hình thang \[IJEF,{\mkern 1mu} \left( {IJ{\rm{//}}EF} \right)\]

Để thiết diện là hình bình hành thì \[IJ = EF \Leftrightarrow \frac{{AB + CD}}{2} = \frac{2}{3}AB\] (do \[\frac{{EF}}{{AB}} = \frac{{SE}}{{SB}} = \frac{{SG}}{{SM}} = \frac{2}{3}\])

\[ \Leftrightarrow 3AB + 3CD = 4AB \Leftrightarrow AB = 3CD\]

Đáp án

a.

Phương trình dạng \[a\sin x + b\cos x = c\]. Chia cả 2 vế cho \[\sqrt {{a^2} + {b^2}} \].

Giải chi tiết:

Ta có:

\[{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} \sqrt 3 \sin 2x + \cos 2x = 2\cos x \Leftrightarrow \frac{{\sqrt 3 }}{2}\sin 2x + \frac{1}{2}\cos 2x = \cos x\]

\[ \Leftrightarrow \sin \frac{\pi }{3}.\sin 2x + \cos \frac{\pi }{3}.\cos 2x = \cos x\]

\[ \Leftrightarrow \cos \left( {2x - \frac{\pi }{3}} \right) = \cos x \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{2x - \frac{\pi }{3} = x + k2\pi }\\{2x - \frac{\pi }{3} = - x + k2\pi }\end{array}} \right. \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = \frac{\pi }{3} + k2\pi }\\{x = \frac{\pi }{9} + k\frac{{2\pi }}{3}}\end{array}} \right.{\mkern 1mu} {\mkern 1mu} \left( {k \in Z} \right)\]

Vậy, phương trình đã cho có nghiệm \[x = \frac{\pi }{3} + k2\pi ,{\mkern 1mu} {\mkern 1mu} x = \frac{\pi }{9} + k\frac{{2\pi }}{3};{\mkern 1mu} {\mkern 1mu} k \in Z\]

b.

Phương pháp giải:

Chọn lần lượt từng chữ số, áp dụng quy tắc cộng và nhân hợp lí.

Giải chi tiết:

Gọi số cần lập là \[\overline {abcdef} ,{\mkern 1mu} \left( {{\mkern 1mu} a,b,c,d,e,f \in \left\{ {0;2;4;5;6;7} \right\},{\mkern 1mu} {\mkern 1mu} a \ne 0} \right)\]

+) \[f = 0\]: có 1 cách chọn

Khi đó: \[a\] có 5 cách chọn

Bộ \[\left( {b,c,d,e} \right)\] có: \[4!\] cách chọn

⇒ Có: \[1.5.4!\] số lập được

+) \[f \in \left\{ {2;4;6} \right\}:\] có 3 cách chọn

Khi đó: a có 4 cách chọn

Bộ \[\left( {b,c,d,e} \right)\] có: \[4!\] cách chọn

⇒ Có: \[3.4.4!\] số lập được

Vậy, số số tự nhiên chẵn và có 6 chữ số đôi một khác nhau có thể lập được là: \[1.5.4! + 3.4.4! = 408\] (số).

c.

Phương pháp giải:

Khai triển nhị thức newton: \[{(x + y)^n} = \sum\limits_{i = 0}^n {C_n^i{x^i}.{y^{n - i}}} \]

Giải chi tiết:

Ta có: \[{\left( {1 + {x^2}} \right)^n} = \sum\limits_{i = 0}^n {C_n^i{x^{2i}}} \]

Tổng các hệ số khai triển: \[\sum\limits_{i = 0}^n {C_n^i} = {\left( {1 + 1} \right)^n} = 512 \Rightarrow {2^n} = {2^9} \Leftrightarrow n = 9\]

Khi đó, \[{\left( {1 + {x^2}} \right)^n} = {\left( {1 + {x^2}} \right)^9} = \sum\limits_{i = 0}^9 {C_9^i{x^{2i}}} \]

Số hạng chứa \[{x^{12}}\] trong khai triển ứng với i thỏa mãn: \[2i = 12 \Leftrightarrow i = 6\]

Hệ số của số hạng chứa \[{x^{12}}\] trong khai triển: \[C_9^6 = 84\].

d.

Phương pháp giải:

Xác suất của biến cố A: \[P\left( A \right) = \frac{{n\left( A \right)}}{{n\left( \Omega \right)}}\]

Giải chi tiết:

Số phần tử của không gian mẫu: \[n\left( \Omega \right) = C_{15}^3\]

Gọi A : “chọn được đúng 2 viên bi màu xanh”

Khi đó

\[n\left( A \right) = C_6^2.C_9^1{\mkern 1mu} {\mkern 1mu} \Rightarrow \]\[P\left( A \right) = \frac{{n\left( A \right)}}{{n\left( \Omega \right)}} = \frac{{C_6^2.C_9^1{\mkern 1mu} }}{{C_{15}^3}} = \frac{{27}}{{91}}\]

Giải chi tiết:

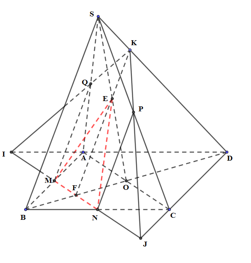
a) Trong (ABCD), gọi \[I = MN \cap AD,\]\[J = MN \cap CD\], \[F = MN \cap BD\]

Trong (SBD), gọi \[K = EF \cap SD\]

Trong (SAD), gọi \[Q = IK \cap SA\]

Trong (SAD), gọi \[P = JK \cap SC\]

Khi đó, thiết diện của hình chóp \[S.ABCD\] cắt bởi mặt phẳng \[\left( {MNE} \right)\] là ngũ giác \[MNPKQ\]

b) MN là đường trung bình của \[\Delta ABC \Rightarrow MN//AC\]

\[ \Rightarrow MF{\rm{//}}AC \Rightarrow \] F là trung điểm của OB \[ \Rightarrow BF = \frac{1}{2}OB = \frac{1}{4}BD \Rightarrow BF = \frac{1}{3}FD\]

Xét \[\Delta SOB\] có: E, F lần lượt là trung điểm của SO, OB \[ \Rightarrow EF\] là đường trung bình của \[\Delta SOB\]

\[ \Rightarrow EF{\rm{//}}SB \Rightarrow FK{\rm{//}}SB \Rightarrow \frac{{KS}}{{KD}} = \frac{{BF}}{{DF}} = \frac{1}{3}\]

Vậy, \[\frac{{KS}}{{KD}} = \frac{1}{3}\]

Phương pháp giải:

\[\sin \left( {a \pm b} \right) = \sin a\cos b \pm \cos a\sin b\]

\[\cos \left( {a \pm b} \right) = \cos a\cos b \mp \sin a\sin b\]

Giải chi tiết:

\[y = \cos 2x + \sin {\mkern 1mu} x - \sqrt 3 \left( {\sin 2x + \cos x} \right) + 3\]\[ \Leftrightarrow y = \left( {\cos 2x - \sqrt 3 \sin 2x} \right) + \left( {\sin {\mkern 1mu} x - \sqrt 3 \cos x} \right) + 3\]

\[ \Leftrightarrow y = - 2\left( {\frac{{ - 1}}{2}\cos 2x + \frac{{\sqrt 3 }}{2}\sin 2x} \right) + 2\left( {\frac{1}{2}\sin {\mkern 1mu} x - \frac{{\sqrt 3 }}{2}\cos x} \right) + 3\]

\[ \Leftrightarrow y = - 2\left( {\cos \frac{{2\pi }}{3}\cos 2x + \sin \frac{{2\pi }}{3}\sin 2x} \right) + 2\left( {\cos \frac{\pi }{3}\sin {\mkern 1mu} x - \sin \frac{\pi }{3}\cos x} \right) + 3\]

\[ \Leftrightarrow y = - 2\cos \left( {2x - \frac{{2\pi }}{3}} \right) + 2\sin \left( {x - \frac{\pi }{3}} \right) + 3\]\[ \Leftrightarrow y = 4{\sin ^2}\left( {x - \frac{\pi }{3}} \right) + 2\sin \left( {x - \frac{\pi }{3}} \right) + 1\]

Ta có: \[x \in \left[ { - \frac{\pi }{3};\frac{\pi }{2}} \right] \Leftrightarrow x - \frac{\pi }{3} \in \left[ { - \frac{{2\pi }}{3};\frac{\pi }{6}} \right]{\mkern 1mu} \]

Khi đó: \[\sin \left( {x - \frac{\pi }{3}} \right) \in \left[ { - \frac{{\sqrt 3 }}{2};\frac{1}{2}} \right]{\mkern 1mu} \Leftrightarrow 2\sin \left( {x - \frac{\pi }{3}} \right) \in \left[ { - \sqrt 3 ;1} \right]{\mkern 1mu} \]

Xét hàm số \[f\left( t \right) = {t^2} + t + 1,{\mkern 1mu} {\mkern 1mu} t \in \left[ { - \sqrt 3 ;1} \right],{\mkern 1mu} {\mkern 1mu} f'\left( t \right) = 2t + 1 = 0 \Leftrightarrow t = - \frac{1}{2}\]

Hàm số \[f\left( t \right)\] liên tục trên đoạn \[\left[ { - \sqrt 3 ;1} \right]\] có \[f\left( { - \sqrt 3 } \right) = 4 - \sqrt 3 ,{\mkern 1mu} {\mkern 1mu} f\left( { - \frac{1}{2}} \right) = \frac{3}{4},{\mkern 1mu} {\mkern 1mu} f\left( 1 \right) = 3\]

\[ \Rightarrow \mathop {\min }\limits_{\left[ { - \sqrt 3 ;1} \right]} f\left( t \right) = f\left( { - \frac{1}{2}} \right) = \frac{3}{4},{\mkern 1mu} {\mkern 1mu} \mathop {\max }\limits_{\left[ { - \sqrt 3 ;1} \right]} f\left( t \right) = f\left( 1 \right) = 3\]\[ \Rightarrow \mathop {\min }\limits_{\left[ { - \frac{\pi }{3};\frac{\pi }{2}} \right]} y = \frac{3}{4},{\mkern 1mu} {\mkern 1mu} \mathop {\max }\limits_{\left[ { - \frac{\pi }{3};\frac{\pi }{2}} \right]} y = 3\]