Bộ 20 đề thi học kì 1 Toán 11 năm 2022 - 2023 có đáp án
Bộ 20 đề thi học kì 1 Toán 11 năm 2022 - 2023 có đáp án (Đề 7)
-
1396 lượt thi
-
27 câu hỏi
-
0 phút
Danh sách câu hỏi
Câu 1:
 Xem đáp án
Xem đáp án
Đáp án B
Phương pháp:
+ Gọi số có 4 chữ số cần lập là ¯abcd(0≤a;b;c;d≤9;a≠0;a,b,c,d∈N).
+ Chọn từng chữ số, sau đó áp dụng quy tắc nhân.
Cách giải:
Gọi số có 4 chữ số cần lập là ¯abcd(0≤a;b;c;d≤9;a≠0;a,b,c,d∈N).
+ Số cần lập là số chẵn ⇒d∈{2;4;6}⇒ Có 3 cách chọn d.
+ Ứng với mỗi cách chọn d có A35=60 cách chọn 3 chữ số a,b,c.
Áp dụng quy tắc nhân ta có: 3.60=180 số thỏa mãn.
Câu 2:
 Xem đáp án
Xem đáp án
Đáp án D
Phương pháp:
Giải phương trình lượng giác cơ bản tanx=tanα⇔x=α+kπ(k∈Z).
Cách giải:
tan2x+√3=0⇔tan2x=−√3⇔2x=−π3+kπ⇔x=−π6+kπ2(k∈Z)
Câu 3:
 Xem đáp án
Xem đáp án
Đáp án C
Phương pháp:
+ Tính số phân tử của không gian mẫu.
+ Tính số phân tử của biến cố.
+ Tính xác suất của biến cố.
Cách giải:
+ Chọn ngẫu nhiên đồng thời 3 quả cầu ⇒n(Ω)=C317=680.
+ Gọi A là biến cố: “Lấy được 3 quả cầu màu xanh” ⇒n(A)=C35=10
Vậy P(A)=n(A)n(Ω)=10680=168
Câu 4:
 Xem đáp án
Xem đáp án
Đáp án C
Phương pháp:
Cho M(x;y) và →u=(a;b), gọi M′(x′;y′)=T→u(M)⇒{x′=x+ay′=y+b
Cách giải:
T→u(A)=B⇔{xB=2+1=3yB=−4−2=−6⇒B(3;−6).
Câu 5:
 Xem đáp án
Xem đáp án
Đáp án D
Phương pháp:
+ Sử dụng định nghĩa phép vị tự: V(I;k)(M)=M′⇔→IM′=k→IM
+ Sử dụng tính chất phép vị tự: Phép vị tự biến đường thẳng thành đường thẳng song song hoặc trùng với nó.
Cách giải:
Gọi d′=V(O;2)(d)⇒d′//d⇒ Phương trình d′ có dạng 3x−2y+c=0.
Lấy A(−1;1)∈d. Gọi A′=V(O;2)⇒→OA′=2→OA⇒{xA′=2.(−1)=−2yA′=2.(−1)=−2⇒A′(−2;−2).
Vì A′∈d′⇒3.(−2)−2.(−2)+c=0⇔c=2.
Vậy d′:3x−2y+2=0.
Câu 6:
 Xem đáp án
Xem đáp án
Đáp án C
Phương pháp:
+ Giải phương trình bậc hai đối với một hàm số lượng giác.
+ Giải phương trình lượng giác cơ bản: sinx=sinα⇔[x=α+k2πx=π−α+k2π(k∈Z)
Cách giải:
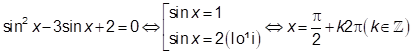
Câu 7:
 Xem đáp án
Xem đáp án
Đáp án A
Phương pháp:
+ Phép tịnh tiến biến đường tròn thành đường tròn có cùng bán kính.
+ Xác định tâm I và bán kính R của đường tròn (C).
+ Gọi I′=Ti(I), xác định tọa độ điểm I′.
+ Gọi (C′)=Ti(C)⇒(C′) là đường tròn có tâm I′ và bán kính R.
Cách giải:
+ Đường tròn (C):(x−1)2+(y+3)2=4 có tâm I(1;−3) và bán kính R=2.
+ Gọi I′=Ti(I)⇒{xI′=1+1=2yI′=−3+0=−3⇒I′(2;−3)
+ Gọi (C′)=Ti(C)⇒(C′) là đường tròn có tâm I′(2;−3) và bán kính R=2.
Vậy phương trình đường tròn (C′):(x−2)2+(y+3)2=4.
Câu 8:
 Xem đáp án
Xem đáp án
Đáp án A
Phương pháp:
Các cách xác định mặt phẳng là:
+ Qua ba điểm không thẳng hàng.
+ Qua một điểm và một đường thẳng không đi qua điểm đó.
+ Qua hai đường thẳng cắt nhau.
+ Qua hai đường thẳng song song.
Cách giải:
Khẳng định sai là đáp án A: Qua ba điểm phân biệt xác định được một và chỉ một mặt phẳng.
Khẳng định đúng phải là: Qua ba điểm phân biệt không thẳng hàng xác định được một và chỉ một mặt phẳng.
Câu 9:
 Xem đáp án
Xem đáp án
Đáp án C
Phương pháp:
{a⊂(α)b⊂(β)a//b⇒ Giao tuyến của hai mặt phẳng (α) và (β) là đường thẳng đi qua điểm chung của hai mặt phẳng và song song với a,b.
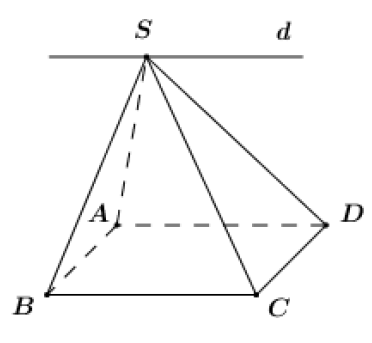
Cách giải:
Xác định (SAD)∩(SBC).
+ S là điểm chung thứ nhất.
+ Ta có {AD⊂(SAD)BC⊂(SBC)AD//BC
Do đó giao tuyến của hai mặt phẳng (SAD) và (SBC) là đường thẳng đi qua S và song song với AD.
Câu 10:
 Xem đáp án
Xem đáp án
Đáp án D
Phương pháp:
Nếu un+1≥un∀n thì dãy số (un) là dãy số tăng.
Cách giải:
Xét dãy số un=2018+2n ta có un+1=2018+2(n+1)=2020+2n>un∀n.
Vạy dãy số un=2018+2n là dãy số tăng.
Câu 11:
 Xem đáp án
Xem đáp án
Đáp án B
Phương pháp:
Phép vị tự tâm I, tỉ số k biến đường tròn bán kính R thành đường tròn có bán kính R′=|k|R.
Cách giải:
Đường tròn (C):(x+1)2+(y−2)2=25 có bán kính R=5.
Phép vị tự tỉ số k=−12 biến đường tròn (C) thành đường tròn có bán kính R′=|−12|R=12.5=52
Câu 12:
 Xem đáp án
Xem đáp án
Đáp án C
Phương pháp:
+ Thay lần lượt n=1,n=2,n=3,.... để tính các số hạng thứ 1, 2, 3, ...
+ (un) dãy số giảm và bị chặn dưới nếu un+1≤un∀n∈N∗ và tồn tại số thực m sao cho un≥m∀n∈N∗.
+ (un) là dãy số tăng nếu un+1≥un∀n∈N∗
Cách giải:
Ta có un+1=1(n+1)2+n+1<1n2+n=un∀n∈N∗⇒(un) là dãy số giảm.
Vậy khẳng định C sai.
Câu 13:
 Xem đáp án
Xem đáp án
Đáp án C
Phương pháp:
Công thức số hạng tổng quát của (un) có số hạng đầu u1 và công sai d là un=u1+(n−1)d
Cách giải:
Công thức số hạng tổng quát của (un) có số hạng đầu u1 và công sai d là un=u1+(n−1)d
Câu 14:
 Xem đáp án
Xem đáp án
Đáp án B
Phương pháp:
Công thức số hạng tổng quát của (un) có số hạng đầu u1 và công sai d là un=u1+(n−1)d
Cách giải:
Công thức số hạng tổng quát của (un) có số hạng đầu u1=3 và công sai d=2 là
un=3+(n−1)2=3+2n−2=2n+1
Câu 15:
 Xem đáp án
Xem đáp án
Đáp án D
Phương pháp:
Sử dụng khai triển nhị thức Newton: (a+b)n=n∑k=0Cknan−kbk(0≤k≤n).
Cách giải:
Ta có: (x2−2x)6=6∑k=0Ck6(x2)6−k(−2x)k=6∑k=0Ck6(−2)kx12−2kx−k=6∑k=0Ck6(−2)kx12−3k
Số hạng không chứa x ứng với 12−3k=0⇔k=4(tm).
Vậy số hạng không chứa x trong khai triển trên là C46.(−2)4=240.
Câu 16:
 Xem đáp án
Xem đáp án
Đáp án D
Phương pháp:
Sử dụng khai triển nhị thức Newton: (a+b)n=n∑k=0Cknan−kbk(0≤k≤n).
Cách giải:
Ta có: (x2−2x)6=6∑k=0Ck6(x2)6−k(−2x)k=6∑k=0Ck6(−2)kx12−2kx−k=6∑k=0Ck6(−2)kx12−3k
Số hạng không chứa x ứng với 12−3k=0⇔k=4(tm).
Vậy số hạng không chứa x trong khai triển trên là C46.(−2)4=240.
Câu 17:
 Xem đáp án
Xem đáp án
Đáp án A
Phương pháp:
+ V(I;k)(M)=M′⇔→IM′=k→IM.
+ T→u(M)=M′⇔→MM′=→u.
Cách giải:
+ Gọi M(x;y)∈d bất kì.
+ Gọi M′(x′;y′)=V(O;−3)(M)⇒{x′=−3xy′=−3y
+ Gọi M″.
+ Do M \in d \Rightarrow 3\frac{{ - x'' + 1}}{3} - 4\frac{{ - y'' + 2}}{3} + 1 = 0 \Leftrightarrow - 3x'' + 4y'' - 2 = 0 \Leftrightarrow 3x'' - 4y'' + 2 = 0.
+ Gọi d' là ảnh của d qua liên tiếp phép vị tự tâm O tỉ số k = - 3 và phép tịnh tiến theo vectơ \overrightarrow u = \left( {1;2} \right).
Ta có
\Rightarrow d':3x - 4y + 2 = 0
Câu 18:
 Xem đáp án
Xem đáp án
Đáp án C
Phương pháp:
Sử dụng công thức tính tổng 1 + 2 + 3 + ... + n = \frac{{n\left( {n + 1} \right)}}{2}
Cách giải:
Ta có:
{u_{n + 1}} = {u_n} + n = {u_{n - 1}} + n + n - 1 = ...
= {u_1} + n + n - 1 + ... + 1
= 2018 + \frac{{\left( {n + 1} \right).n}}{2}
Vậy {u_n} = 2018 + \frac{{n\left( {n - 1} \right)}}{2}.
Câu 19:
 Xem đáp án
Xem đáp án
Đáp án C
Phương pháp:
+ Sử dụng công thức hạ bậc {\cos ^2}x = \frac{{1 + \cos 2x}}{2}
+ Sử dụng phương pháp giải phương trình dạng a\sin x + b\cos x.
Cách giải:
4{\cos ^2}\frac{x}{2} - \sqrt 3 \cos 2x = 1 + 2{\cos ^2}\left( {x - \frac{\pi }{4}} \right) \Leftrightarrow 2\left( {1 + \cos x} \right) - \sqrt 3 \cos 2x = 1 + 1 + \cos \left( {2x - \frac{\pi }{2}} \right)
\Leftrightarrow 2 + 2\cos x - \sqrt 3 \cos 2x = 2 + \sin 2x \Leftrightarrow 2\cos x = \sin 2x + \sqrt 3 \cos 2x
\Leftrightarrow \cos x = \frac{1}{2}\sin 2x + \frac{{\sqrt 3 }}{2}\cos 2x \Leftrightarrow \cos x = \cos 2x.\cos \frac{\pi }{6} + \sin 2x.\sin \frac{\pi }{6}
\Leftrightarrow \cos x = \cos \left( {2x - \frac{\pi }{6}} \right) \Leftrightarrow \left[ \begin{array}{l}2x - \frac{\pi }{6} = x + k2\pi \\2x - \frac{\pi }{6} = - x + k2\pi \end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = \frac{\pi }{6} + k2\pi \\x = \frac{\pi }{{18}} + \frac{{k2\pi }}{3}\end{array} \right.\left( {k \in \mathbb{Z}} \right)
Các nghiệm của phương trình thuộc \left( {0;\frac{\pi }{2}} \right) là \left\{ {\frac{\pi }{6};\frac{\pi }{{18}}} \right\}
Câu 20:
 Xem đáp án
Xem đáp án
Đáp án C
Phương pháp:
+ Đặt t = \sin x - \sqrt 3 \cos x, tìm khoảng giá trị của t.
+ Đưa hàm số về ẩn t trên miền giá trị đã xác định được, lập BBT và kết luận.
Cách giải:
y = \sqrt {{{\left( {\sin x - \sqrt 3 \cos x} \right)}^2} - 2\sin x + 2\sqrt 3 \cos x - m + 3}
y = \sqrt {{{\left( {\sin x - \sqrt 3 \cos x} \right)}^2} - 2\left( {\sin x - \sqrt 3 \cos x} \right) - m + 3}
+ Đặt t = \sin x - \sqrt 3 \cos x = 2\left( {\frac{1}{2}\sin x - \frac{{\sqrt 3 }}{2}\cos x} \right) = 2\sin \left( {x - \frac{\pi }{3}} \right) \Rightarrow - 2 \le t \le 2
Khi đó hàm số trở thành y = \sqrt {{t^2} - 2t - m + 3} \,\,\forall t \in \left[ { - 2;2} \right]\,\,\left( * \right).
+ Để hàm số ban đầu xác định với mọi x \in \mathbb{R} thì hàm số xác định với mọi t \in \left[ { - 2;2} \right].
Tức là {t^2} - 2t - m + 3 \ge 0\,\,\forall t \in \left[ { - 2;2} \right].
+ Xét hàm số f\left( t \right) = {t^2} - 2t - m + 3 trên \left[ { - 2;2} \right] ta có BBT:
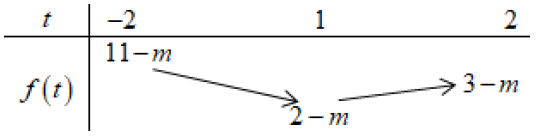
Để {t^2} - 2t - m + 3 \ge 0\,\,\forall t \in \left[ { - 2;2} \right] thì 2 - m \ge 0 \Leftrightarrow m \le 2.
Mà m nguyên dương \Rightarrow m \in \left\{ {1;2} \right\}.
Chú ý: Cần xác định chính xác khoảng giá trị của t.
Câu 21:
 Xem đáp án
Xem đáp án
Đáp án C
Phương pháp:
+ Tính số phần tử của không gian mẫu.
+ Tính số phần tử của biến cố.
+ Tính xác suất của biến cố.
Cách giải:
Xếp ngẫu nhiên 6 chữ cái trên thành hàng ngang có \frac{{6!}}{{2!.2!}} = 180 cách \Rightarrow n\left( \Omega \right) = 180.
Buộc các chữ cái H, H thành 1 buộc, S, S thành một buộc, khi đó ta cần xếp các chữ cái \left( {HH} \right),\,\,\left( {SS} \right),\,\,V,\,\,N thành 1 hàng ngang, có 4! = 24 cách.
Gọi A là biến cố: “2 chữ cái giống nhau đứng cạnh nhau” \Rightarrow n\left( A \right) = 24.
Vậy P\left( A \right) = \frac{{n\left( A \right)}}{{n\left( \Omega \right)}} = \frac{{24}}{{180}} = \frac{2}{{15}}.
Câu 22:
1) Giải các phương trình sau:
a) 2\sin x + \sqrt 2 = 0;
b) \sqrt 3 \sin x - \cos x + 2 = 0;
 Xem đáp án
Xem đáp án
1) 2\sin x + \sqrt 2 = 0
Phương pháp:
Giải phương trình lượng giác cơ bản: \sin x = \sin \alpha \Leftrightarrow \left[ \begin{array}{l}x = \alpha + k2\pi \\x = \pi - \alpha + k2\pi \end{array} \right.\left( {k \in \mathbb{Z}} \right)
Cách giải:
2\sin x + \sqrt 2 = 0 \Leftrightarrow \sin x = - \frac{{\sqrt 2 }}{2} \Leftrightarrow \left[ \begin{array}{l}x = - \frac{\pi }{4} + k2\pi \\x = \frac{{5\pi }}{4} + k2\pi \end{array} \right.\left( {k \in \mathbb{Z}} \right).
Câu 23:
2) Tìm giá trị lớn nhất của hàm số y = 2\sqrt {\sin x + 1} - 3.
 Xem đáp án
Xem đáp án
2) \sqrt 3 \sin x - \cos x + 2 = 0.
Phương pháp:
Chia cả hai vế của phương trình cho \sqrt {{a^2} + {b^2}} .
Cách giải:
\sqrt 3 \sin x - \cos x + 2 = 0 \Leftrightarrow \frac{{\sqrt 3 }}{2}\sin x - \frac{1}{2}\cos x = - 1
\Leftrightarrow \sin x\cos \frac{\pi }{6} - \cos x\sin \frac{\pi }{6} = - 1 \Leftrightarrow \sin \left( {x - \frac{\pi }{6}} \right) = - 1
\Leftrightarrow x - \frac{\pi }{6} = - \frac{\pi }{2} + k2\pi \Leftrightarrow x = - \frac{\pi }{3} + k2\pi \left( {k \in \mathbb{Z}} \right)
Câu 24:
1) Cho tập hợp A = \left\{ {0;1;2;3;4;5;6;7;8;9} \right\}. Có bao nhiêu số tự nhiên có 4 chữ số được thành lập từ tập hợp A.
 Xem đáp án
Xem đáp án
1) Cho tập hợp A = \left\{ {0;1;2;3;4;5;6;7;8;9} \right\}. Có bao nhiêu số tự nhiên có 4 chữ số được thành lập từ tập hợp A.
Phương pháp:
+ Gọi số tự nhiên có 4 chữ số cần lập là \overline {abcd} \left( {0 \le a;b;c;d \le 9;\,\,a \ne 0;\,\,a,b,c,d \in \mathbb{N}} \right).
+ Tìm số cách chọn từng chữ số, sau đó áp dụng quy tắc nhân.
Cách giải:
Gọi số tự nhiên có 4 chữ số cần lập là \overline {abcd} \left( {0 \le a;b;c;d \le 9;\,\,a \ne 0;\,\,a,b,c,d \in \mathbb{N}} \right).
+ a \ne 0 \Rightarrow Có 9 cách chọn a.
+ 3 chữ số còn lại, mỗi số có 10 cách chọn.
Áp dụng quy tắc nhân ta có: {9.10^3} = 9000 số.
Câu 25:
2) Một hộp có 6 bi đỏ, 7 bi xanh, 8 bi vàng (các bi khác nhau). Lấy ngẫu nhiên 6 bi. Tính xác suất để lấy được ít nhất 3 bi đỏ.
 Xem đáp án
Xem đáp án
2) Một hộp có 6 bi đỏ, 7 bi xanh, 8 bi vàng (các bi khác nhau). Lấy ngẫu nhiên 6 bi. Tính xác suất để lấy được ít nhất 3 bi đỏ.
Phương pháp:
Sử dụng biến cố đối.
Cách giải:
Lấy ngẫu nhiên 6 viên bi \Rightarrow n\left( \Omega \right) = C_{21}^6 = 54264.
Gọi A là biến cố: “Lấy được ít nhất 3 viên bi đỏ” \Rightarrow \overline A : “Lấy được ít hơn 3 viên bi đỏ”.
TH1: 0 bi đỏ + 6 bi khác màu đỏ (xanh hoặc vàng).
Số cách chọn là: C_6^0.C_{15}^6 = 5005 cách.
TH2: 1 bi đỏ + 5 bi khác màu đỏ (xanh hoặc vàng).
Số cách chọn là: C_6^1.C_{15}^5 = 18018 cách.
TH3: 2 bi đỏ + 4 bi khác màu đỏ (xanh hoặc vàng).
Số cách chọn là: C_6^2.C_{15}^4 = 20475 cách.
Áp dụng quy tắc cộng ta có n\left( {\overline A } \right) = 5005 + 18018 + 20475 = 43498.
Vậy P\left( A \right) = 1 - P\left( {\overline A } \right) = 1 - \frac{{43498}}{{54264}} = \frac{{769}}{{3876}}.
Câu 26:
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi O là giao điểm của AC và BD. M và N lần lượt là trung điểm của CD và SA. G là trọng tâm tam giác SAB.
1) Tìm giao tuyến của hai mặt phẳng \left( {SAC} \right) và \left( {SBD} \right).
2) Chứng minh MN song song với mặt phẳng \left( {SBC} \right).
3) Gọi \Delta là giao tuyến của hai mặt phẳng \left( {SAD} \right) và \left( {SMG} \right), P là giao điểm của đường thẳng OG và \Delta . Chứng minh P,N,D thẳng hàng.
 Xem đáp án
Xem đáp án
Phương pháp:
1) Xác định hai điểm chung của hai mặt phẳng.
2) + Gọi Q là trung điểm của SB.
+ Chứng minh MN song song với một đường thẳng bất kì chứa trong \left( {SBC} \right).
3) + Xác định \Delta .
+ Xác định giao tuyến của \left( {SAD} \right) và \left( {BDG} \right).
+ Chứng minh P là điểm chung của hai mặt phẳng \left( {SAD} \right) và \left( {BDG} \right).
Cách giải:
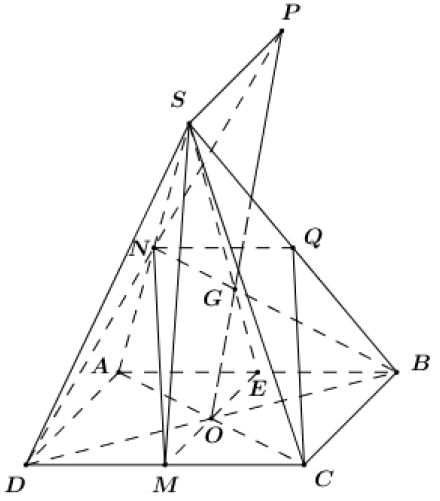
1) Tìm \left( {SAC} \right) \cap \left( {SBD} \right).
+ S là điểm chung thứ nhất.
+ Trong \left( {ABCD} \right) có AC \cap BD = 0, ta có:
\left\{ \begin{array}{l}O \in AC \subset \left( {SAC} \right) \Rightarrow O \in \left( {SAC} \right)\\O \in BD \subset \left( {SBD} \right) \Rightarrow O \in \left( {SBD} \right)\end{array} \right. \Rightarrow O \in \left( {SAC} \right) \cap \left( {SBD} \right)
\Rightarrow O là điểm chung thứ hai.
Vậy \left( {SAC} \right) \cap \left( {SBD} \right) = SO.
2) Gọi Q là trung điểm của SB.
NQ là đường trung bình của tam giác SAB \Rightarrow NQ//AB và NQ = \frac{1}{2}AB.
\Rightarrow NQ//MC và NQ = MC \Rightarrow MNQC là hình bình hành (dhnb).
\Rightarrow MN//QC. Mà QC \subset \left( {SAB} \right).
Vậy MN//\left( {SAB} \right).
3) Gọi E là trung điểm của AB ta có \left( {SMG} \right) \equiv \left( {SME} \right).
Xác định \left( {SAD} \right) \cap \left( {SME} \right).
+ S là điểm chung thứ nhất.
+ \left\{ \begin{array}{l}AD \subset \left( {SAD} \right)\\ME \subset \left( {SME} \right)\\AD//ME\end{array} \right.
\Rightarrow Giao tuyến của hai mặt phẳng \left( {SAD} \right) và \left( {SME} \right) là đường thẳng đi qua S và song song với
AD,\,\,ME.
Qua S dựng đường thẳng song song với AD cắt OG tại P \Rightarrow \Delta \equiv SP.
Nội BN ta có \left( {SAD} \right) \cap \left( {BDN} \right) = DN.
\left\{ \begin{array}{l}P \in \Delta = \left( {SAD} \right) \cap \left( {SBC} \right) \Rightarrow P \in \left( {SAD} \right)\\P \in OQ \subset \left( {BDG} \right) \Rightarrow P \in \left( {BDG} \right)\end{array} \right. \Rightarrow P \in \left( {SAD} \right) \cap \left( {BDG} \right)
Vậy P \in DN hay P,N,D thẳng hàng.
Câu 27:
 Xem đáp án
Xem đáp án
Phương pháp:
+ Tính số phần tử của không gian mẫu.
+ Tính số phần tử của biến cố.
+ Tính xác suất của biến cố.
Cách giải:
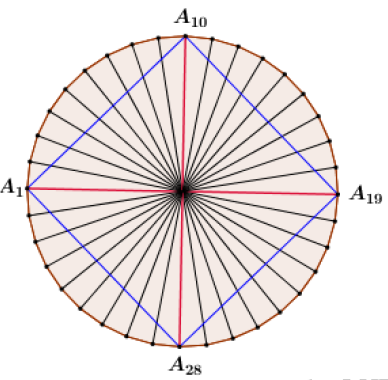
Chọn ngẫu nhiên 4 đỉnh của hình \left( H \right) \Rightarrow n\left( \Omega \right) = C_{36}^4 = 58905.
Giả sử {A_1},{A_2},{A_3},...,{A_{36}} là 36 đỉnh của đa giác đều \left( H \right). Gọi O là tâm của đa giác đều \left( H \right).
\Rightarrow {A_1}{A_2}...{A_{36}} là đa giác đều ngoại tiếp đường tròn \left( O \right).
Khi đó ta có {A_i}O{A_{i + 1}} = \frac{{360^\circ }}{{36}} = 10^\circ \,\,\forall i = \overline {1;36} .
Để {A_x}{A_y}{A_z}{A_t} là hình vuông thì {A_x}O{A_y} = {A_y}O{A_z} = {A_z}O{A_t} = {A_t}O{A_x} = 90^\circ .
Ta có {O_1}O{A_{10}} = {A_{10}}O{A_{19}} = {A_{19}}O{A_{28}} = {A_{28}}O{A_1} = 90^\circ \Rightarrow {A_1}{A_{10}}{A_{19}}{A_{28}} là 1 hình vuông.
Cứ như vậy ta có các hình vuông là {A_2}{A_{11}}{A_{20}}{A_{29}},\,\,{A_3}{A_{12}}{A_{21}}{A_{30}},...,{A_9}{A_{18}}{A_{27}}{A_{36}}.
Gọi A là biến cố: “4 đỉnh được chọn tạo thành hình vuông” \Rightarrow n\left( A \right) = 9.
Vậy P\left( A \right) = \frac{9}{{58905}} = \frac{1}{{6564}}.
