Bộ 20 đề thi học kì 1 Toán 11 năm 2022 - 2023 có đáp án
Bộ 20 đề thi học kì 1 Toán 11 năm 2022 - 2023 có đáp án (Đề 11)
-
880 lượt thi
-
22 câu hỏi
-
0 phút
Danh sách câu hỏi
Câu 1:
 Xem đáp án
Xem đáp án
Đáp án A.
Phương pháp:
\(\tan x\) xác định \( \Leftrightarrow x \ne \frac{\pi }{2} + k\pi \,\left( {k \in \mathbb{Z}} \right)\).
Cách giải:
ĐKXĐ: \(\cos x \ne 0 \Leftrightarrow x \ne \frac{\pi }{2} + k\pi ,\,k \in \mathbb{Z}\).
TXĐ: \(D = \left\{ {x \in \mathbb{R},\,x \ne \frac{\pi }{2} + k\pi ,\,\,k \in \mathbb{Z}} \right\}\).
Câu 2:
 Xem đáp án
Xem đáp án
Đáp án C
Phương pháp:
Sử dụng công thức tổ hợp.
Cách giải:
Số cách chọn 6 học sinh đổi trực nhật từ một lớp 50 học sinh là: \(C_{50}^6\)
Câu 3:
 Xem đáp án
Xem đáp án
Đáp án D
Phương pháp:
Số đường chéo của một đa giác n đỉnh là \(C_n^2 - n,\,\,n \in \mathbb{N},\,\,n \ge 3\).
Cách giải:
Số đường chéo của một đa giác n đỉnh là \(C_n^2 - n,\,\,n \in \mathbb{N},\,\,n \ge 3\)
Theo đề bài, ta có: \(C_n^2 - n = 35 \Leftrightarrow \frac{{n\left( {n - 1} \right)}}{2} - n = 35 \Leftrightarrow {n^2} - 3n - 70 = 0 \Leftrightarrow \left[ \begin{array}{l}n = 10\,\left( {TM} \right)\\n = - 7\,\left( L \right)\end{array} \right.\)
Vậy, đa giác đó có 10 đỉnh.
Câu 4:
 Xem đáp án
Xem đáp án
Đáp án A
Phương pháp:
Phép tịnh tiến theo \(\overrightarrow \nu \) biến đường thẳng d thành chính nó khi và chỉ khi vectơ \(\overrightarrow \nu \) có giá trị song song hoặc trùng với đường thẳng d.
Cách giải:
Đường thẳng d: \(2{\rm{x}} - y + 1 = 0\) có 1 VTCP: \(\overrightarrow u = \left( {1;\,2} \right)\)
Ta có: \(\overrightarrow \nu = \left( {2;\,\,4} \right)\)cùng phương với \(\overrightarrow u = \left( {1;\,2} \right)\)\( \Rightarrow \overrightarrow \nu = \left( {2;\,\,4} \right)\) có giá song song hoặc trùng với đường thẳng d
\( \Rightarrow \)Phép tịnh tiến theo vectơ \(\overrightarrow \nu = \left( {2;\,\,4} \right)\) biến d thành chính nó.
Câu 5:
 Xem đáp án
Xem đáp án
Đáp án A
Phương pháp:
Áp dụng Công thức khai triển nhị thức Newton: \({\left( {x + y} \right)^n} = \sum\limits_{i = 0}^n {C_n^i{x^i}.{y^{n - i}}} \).
Cách giải:
Hệ số của \({x^5}\) trong khai triển \(x{\left( {2{\rm{x}} - 1} \right)^6} + {\left( {3{\rm{x}} - 1} \right)^8}\) bằng tổng hệ số của \({x^4}\) trong khai triển \({\left( {2{\rm{x}} - 1} \right)^6}\) và hệ số của \({x^5}\) trong khai triển \({\left( {3{\rm{x}} - 1} \right)^8}\).
+) \({\left( {2{\rm{x}} - 1} \right)^6} = \sum\limits_{i = 0}^6 {C_6^i{{\left( {2{\rm{x}}} \right)}^i}.{{\left( { - 1} \right)}^{6 - i}} = \sum\limits_{i = 0}^6 {C_6^i{2^i}{{\left( { - 1} \right)}^{6 - i}}{x^i}} } \).
Hệ số của \({x^4}\) trong khai triển \({\left( {2{\rm{x}} - 1} \right)^6}\) ứng với \(i = 4\) và bằng \(C_6^4{2^4}{\left( { - 1} \right)^{6 - 4}} = 240\).
+) \({\left( {{\rm{3x}} - 1} \right)^8} = \sum\limits_{k = 0}^8 {C_8^k{{\left( {3{\rm{x}}} \right)}^k}.{{\left( { - 1} \right)}^{8 - k}} = \sum\limits_{k = 0}^8 {C_8^k{3^k}{{\left( { - 1} \right)}^{8 - k}}{x^k}} } \).
Hệ số của \({x^5}\) trong khai triển \({\left( {3{\rm{x}} - 1} \right)^8}\) ứng với \(k = 5\) và bằng \(C_8^5{3^5}{\left( { - 1} \right)^{6 - 3}} = - 13608\)
\( \Rightarrow \)Hệ số của \({x^5}\) trong khai triển \(x{\left( {2{\rm{x}} - 1} \right)^6} + {\left( {3{\rm{x}} - 1} \right)^8}\) là: \(240 - 13608 = - 13368\).
Câu 6:
 Xem đáp án
Xem đáp án
Đáp án A
Phương pháp:
Phép vị tự tâm O tỉ số k biến \(M\left( {x;\,y} \right) \mapsto M'\left( {x';\,\,y'} \right) \Leftrightarrow \left\{ \begin{array}{l}x' = k{\rm{x}}\\y' = ky\end{array} \right.\).
Phép quay tâm O góc quay \(180^\circ \) biến \(M\left( {x;\,y} \right) \mapsto M'\left( {x';\,\,y'} \right) \Leftrightarrow \left\{ \begin{array}{l}x' = - {\rm{x}}\\y' = - y\end{array} \right.\).
Cách giải:
Lấy \(M\left( {x;\,y} \right) \in \left( C \right):{\left( {x - 2} \right)^2} + {\left( {y - 2} \right)^2} = 4\)
Phép vị tự tâm O tỉ số \(k = \frac{1}{2}\) biến \(M\left( {x;\,y} \right) \mapsto M'\left( {x';\,\,y'} \right) \Leftrightarrow \left\{ \begin{array}{l}x' = \frac{1}{2}{\rm{x}}\\y' = \frac{1}{2}y\end{array} \right.\).
Phép quay tâm O góc quay \(180^\circ \) biến \(M'\left( {x';\,y'} \right) \mapsto M''\left( {x'';\,\,y''} \right) \Leftrightarrow \left\{ \begin{array}{l}x'' = - x'\\y'' = - y'\end{array} \right.\).
\( \Rightarrow \left\{ \begin{array}{l}x'' = - \frac{1}{2}{\rm{x}}\\y'' = - \frac{1}{2}y\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = - 2{\rm{x''}}\\y = - 2y''\end{array} \right.\)
\( \Rightarrow {\left( {2{\rm{x''}} - 2} \right)^2} + {\left( {2y'' - 2} \right)^2} = 4 \Leftrightarrow {\left( {x'' - 1} \right)^2} + {\left( {y'' - 1} \right)^2} = 1\)
Vậy phương trình của đường tròn cần tìm là \({\left( {x - 1} \right)^2} + {\left( {y - 1} \right)^2} = 1\).
Câu 7:
 Xem đáp án
Xem đáp án
Đáp án B
Phương pháp:
Xác định 2 điểm phân biệt cùng thuộc cả hai mặt phẳng. Từ đó kết luận giao tuyến.
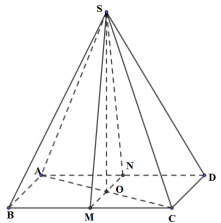
Cách giải:
Gọi O là tâm của hình bình hành ABCD Þ O là trung điểm của AC.
Ta có:
ON là đường trung bình của \(\Delta AC{\rm{D}} \Rightarrow ON//C{\rm{D}}\)
OM là đường trung bình của \(\Delta ABC \Rightarrow OM//AB\)
Mà \(AB//C{\rm{D}} \Rightarrow OM//C{\rm{D}} \Rightarrow \) O, M, N thẳng hàng
\( \Rightarrow {\rm{AC}} \cap {\rm{MN = O}} \Rightarrow {\rm{O}} \in \left( {SAC} \right) \cap \left( {SMN} \right)\)
Mà \(S \in \left( {SAC} \right) \cap \left( {SMN} \right) \Rightarrow \left( {SAC} \right) \cap \left( {SMN} \right) = SO\).
Câu 8:
 Xem đáp án
Xem đáp án
Đáp án C
Phương pháp:
Áp dụng \(C_n^0 + C_n^1 + ... + C_n^n = {2^n}\).
Cách giải:
Ta có: \(C_{2019}^0 + C_{2019}^1 + C_{2019}^2 + C_{2019}^3 + ... + C_{2019}^{2019} = {2^{2019}}\)
Mà \(C_{2019}^0 = C_{2019}^{2019} = 1,\,\,C_{2019}^1 = C_{2019}^{2018},\,C_{2019}^2 = C_{2019}^{2017},...,C_{2019}^{1009} = C_{2019}^{1010}\)
\( \Leftrightarrow 1 + C_{2019}^1 + C_{2019}^2 + C_{2019}^3 + ... + C_{2019}^{1009} + C_{2019}^{1010} + ... + C_{2019}^1 + 1 = {2^{2019}}\)
\( \Leftrightarrow 2 + 2\left( {C_{2019}^1 + C_{2019}^2 + C_{2019}^3 + ... + C_{2019}^{1009}} \right) = {2^{2019}}\)
\( \Leftrightarrow C_{2019}^1 + C_{2019}^2 + C_{2019}^3 + ... + C_{2019}^{1009} = {2^{2018}} - 1\).
Câu 9:
 Xem đáp án
Xem đáp án
Đáp án B
Phương pháp:
Áp dụng công thức cộng và nhân xác suất.
Cách giải:
Xác suất để không có ai bắn trúng là: \(\left( {1 - 0,8} \right)\left( {1 - 0,6} \right) = 0,2.0,4 = 0,08\).
Xác suất để có ít nhất một người bắn trúng là: \(1 - 0,08 = 0,92\).
Câu 10:
 Xem đáp án
Xem đáp án
Đáp án A
Phương pháp:
\({\sin ^6}x + {\cos ^6}x = {\left( {{{\sin }^2}x + {{\cos }^2}x} \right)^3} - 3{\sin ^2}x.{\cos ^2}x.\left( {{{\sin }^2}x + {{\cos }^2}x} \right) = 1 - 3{\sin ^2}x.{\cos ^2}x\)
\({\sin ^2}x = \frac{{1 - \cos 2x}}{2};\,\,{\cos ^2}x = \frac{{1 + \cos 2x}}{2}\)
Cách giải:
Ta có: \({\sin ^6}x + {\cos ^6}x = {\cos ^2}2x + m \Leftrightarrow 1 - 3{\sin ^2}x.{\cos ^2}x = {\cos ^2}2x + m \Leftrightarrow 1 - \frac{3}{4}{\sin ^2}2x = {\cos ^2}2x + m\)
\( \Leftrightarrow 1 - \frac{3}{4}.\frac{{1 - \cos 4x}}{2} = \frac{{1 + \cos 4x}}{2} + m \Leftrightarrow 8 - 3 + 3\cos 4x = 4 + 4\cos 4x + 8m \Leftrightarrow \cos 4x = 1 - 8m\)
Do \(x \in \left[ {0;\,\,\frac{\pi }{8}} \right] \Rightarrow 4x \in \left[ {0;\,\,\frac{\pi }{2}} \right] \Rightarrow 0 \le \cos 4x \le 1\).
Để phương trình đã cho có nghiệm thì \(0 \le 1 - 8m \le 1 \Leftrightarrow 0 \le m \le \frac{1}{8}\).
Câu 11:
 Xem đáp án
Xem đáp án
Đáp án D
Phương pháp:
Xác suất của biến cố A là: \(P\left( A \right) = \frac{{n\left( A \right)}}{{n\left( \Omega \right)}}\).
Cách giải:
Số phần tử của không gian mẫu: \(n\left( \Omega \right) = 30!\)
Số cách xếp An và Hà đứng cạnh nhau là: 2 (cách).
Khi đó, coi An và Hà là 1 nhóm. Số cách hoán vị nhóm (An, Hoài) và 28 bạn còn lại là: 29!
\( \Rightarrow \) Số cách xếp để hai bạn An và Hà đứng cạnh nhau là: \(2.29!\)
\( \Rightarrow \)Xác suất để hai bạn An và Hà đứng cạnh nhau là: \(\frac{{2.29!}}{{30!}} = \frac{1}{{15}}\).
Câu 12:
 Xem đáp án
Xem đáp án
Đáp án C
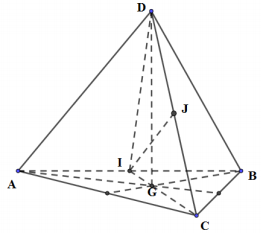
Cách giải:
Gọi I, J lần lượt là trung điểm của AB, CD \( \Rightarrow \) I, G, C thẳng hàng.
\( \Rightarrow \)(CGD) cắt tứ diện ABCD bởi thiết diện là tam giác ICD
Ta có: \(I{\rm{D}} = IC = \frac{{a\sqrt 3 }}{2}\) (do là đường cao của tam giác đều cạnh a)
\( \Rightarrow \Delta IC{\rm{D}}\) cân tại I \( \Rightarrow IJ \bot CD\)
\(\Delta IJC\) vuông tại J \( \Rightarrow IJ = \sqrt {I{C^2} - J{C^2}} = \sqrt {{{\left( {\frac{{a\sqrt 3 }}{2}} \right)}^2} - {{\left( {\frac{a}{2}} \right)}^2}} = \frac{{a\sqrt 2 }}{2}\)
Diện tích \(\Delta IC{\rm{D}}\) là: \(S = \frac{1}{2}IJ.CD = \frac{1}{2}.\frac{{a\sqrt 2 }}{2}.a = \frac{{{a^2}\sqrt 2 }}{4}\).
Câu 13:
 Xem đáp án
Xem đáp án
Đáp án B
Phương pháp:
Phương trình dạng: \(a\sin x + b\cos x = c\) có nghiệm \( \Leftrightarrow {a^2} + {b^2} \ge {c^2}\)
Cách giải:
TXĐ: \(D = \mathbb{R}\)
Gọi \({y_0}\) là một giá trị của hàm số \(y = \frac{{2\sin 2x + \cos 2x}}{{\sin 2x - \cos 2x + 3}}\), khi đó tồn tại \({x_0}\) để \({y_0} = \frac{{2\sin 2{x_0} + \cos 2{x_0}}}{{\sin 2{x_0} - \cos 2{x_0} + 3}}\)
\( \Leftrightarrow {y_0}.\left( {\sin 2{x_0} - \cos 2{x_0} + 3} \right) = 2\sin 2{x_0} + \cos 2{x_0} \Leftrightarrow \left( {{y_0} - 2} \right).\sin 2{x_0} - \left( {{y_0} + 1} \right).\cos 2{x_0} = - 3{y_0}\) (*)
(*) tồn tại \( \Leftrightarrow {\left( {{y_0} - 2} \right)^2} + {\left( {{y_0} + 1} \right)^2} \ge {\left( {3{y_0}} \right)^2} \Leftrightarrow 7y_0^2 + 2{y_0} - 5 \le 0 \Leftrightarrow - 1 \le {y_0} \le \frac{5}{7}\)
Þ Tập giá trị của hàm số \(y = \frac{{2\sin 2x + \cos 2x}}{{\sin 2x - \cos 2x + 3}}\) là \(T = \left[ { - 1;\,\,\frac{5}{7}} \right]\).
Tập giá trị T có các giá trị nguyên là: -1; 0 (hai giá trị)
Câu 14:
 Xem đáp án
Xem đáp án
Đáp án A
Phương pháp:
Xác suất của biến cố A là: \(P\left( A \right) = \frac{{n\left( A \right)}}{{n\left( \Omega \right)}}\).
Cách giải:
Số phần tử của không gian mẫu: \(n\left( \Omega \right) = C_{16}^4\)
Gọi A: “4 thẻ được chọn đều là số chẵn”
\( \Rightarrow n\left( A \right) = C_8^4 \Rightarrow P\left( A \right) = \frac{{n\left( A \right)}}{{n\left( \Omega \right)}} = \frac{{C_8^4}}{{C_{16}^4}} = \frac{1}{{26}}\).
Câu 15:
 Xem đáp án
Xem đáp án
Đáp án D
Phương pháp:
Xác định thiết diện dựa vào các yếu tố song song.
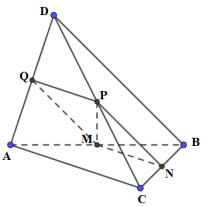
Cách giải:
Gọi Q là trung điểm của AD.
Ta có: \(PQ//AC\) (do PQ là đường trung bình của tam giác ACD)
\(MN//AC\) (do MN là đường trung bình của tam giác ABC).
\( \Rightarrow PQ//MN \Rightarrow \) M, N, P, Q đồng phẳng \( \Rightarrow \)\(Q \in \left( {MNP} \right)\)
\( \Rightarrow \)Thiết diện của tứ diện cắt bởi mặt phẳng (MNP) là tứ giác MNQP.
Ta có: \(PQ//MN,\,PQ = MN\left( { = \frac{1}{2}AC} \right) \Rightarrow \)MNQP là hình bình hành
Vậy, thiết diện của tứ diện cắt bởi mp(MNP) là hình bình hành.
Câu 16:
 Xem đáp án
Xem đáp án
Đáp án B
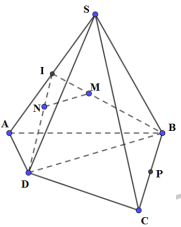
Phương pháp:
\(\left\{ \begin{array}{l}a//b\\b \subset \left( \alpha \right) \Rightarrow a//\left( \alpha \right)\\a \not\subset \left( \alpha \right)\end{array} \right.\)
Cách giải:
Gọi I là trung điểm của tam giác IBD.
Do M, N lần lượt là trọng tâm của tam giác SAB, SAD nên ta có:
\(\frac{{IN}}{{I{\rm{D}}}} = \frac{{IM}}{{IB}} = \frac{1}{3} \Rightarrow MN//B{\rm{D}}\)
Mà \(B{\rm{D}} \subset \left( {SB{\rm{D}}} \right),\,\,MN \not\subset \left( {SB{\rm{D}}} \right) \Rightarrow MN//\left( {SB{\rm{D}}} \right)\).
Câu 17:
Giải các phương trình sau:
a) \(\frac{3}{{{{\sin }^2}x}} - 2\sqrt 3 \cot x - 6 = 0\)
 Xem đáp án
Xem đáp án
Phương pháp:
- Tìm ĐKXĐ
- Sử dụng công thức \(\frac{1}{{{{\sin }^2}x}} = 1 + {\cot ^2}x\), biến đổi phương trình về dạng phương trình bậc hai đối với \(\cot x\).
Cách giải:
ĐKXĐ: \(\sin x \ne 0 \Leftrightarrow x \ne k\pi ,\,k \in \mathbb{Z}\)
Ta có:
\(\frac{3}{{{{\sin }^2}x}} - 2\sqrt 3 \cot x - 6 = 0 \Leftrightarrow 3\left( {1 + {{\cot }^2}x} \right) - 2\sqrt 3 \cot x - 6 = 0\)
\( \Leftrightarrow 3{\cot ^2}x - 2\sqrt 3 \cot x - 3 = 0 \Leftrightarrow \left[ \begin{array}{l}\cot x = \sqrt 3 \\\cot x = - \frac{1}{{\sqrt 3 }}\end{array} \right.\)
\( \Leftrightarrow \left[ \begin{array}{l}x = \frac{\pi }{6} + k\pi \\x = - \frac{\pi }{3} + k\pi \end{array} \right.,\,k \in \mathbb{Z}\) (thỏa mãn ĐKXĐ)
Vậy phương trình đã cho có nghiệm \(x = \frac{\pi }{6} + k\pi ,\,x = - \frac{\pi }{3} + k\pi ,\,\,k \in \mathbb{Z}\,\).
Câu 18:
 Xem đáp án
Xem đáp án
Phương pháp:
- Tìm ĐKXĐ
- Biến đổi phương trình về phương trình cơ bản để giải.
Cách giải:
ĐKXĐ: \(1 - 2\sin x \ne 0 \Leftrightarrow \sin x \ne \frac{1}{2} \Leftrightarrow \left\{ \begin{array}{l}x \ne \frac{\pi }{6} + k2\pi \\x \ne \frac{{5\pi }}{6} + k2\pi \end{array} \right.,\,k \in \mathbb{Z}\).
Khi đó:
\[\frac{{\cos \left( {\frac{{7\pi }}{2} - 2x} \right) - \sqrt 3 \cos \left( {2x - 3\pi } \right) + 2\cos x}}{{1 - 2\sin x}} = 0\]
\[ \Leftrightarrow \cos \left( {3\pi + \frac{\pi }{2} - 2x} \right) - \sqrt 3 \cos \left( {2x - 3\pi } \right) + 2\cos x = 0\]
\[ \Leftrightarrow - \cos \left( {\frac{\pi }{2} - 2x} \right) + \sqrt 3 \cos 2x + 2\cos x = 0\]
\[ \Leftrightarrow - \sin 2x + \sqrt 3 \cos 2x + 2cosx = 0\]
\[ \Leftrightarrow \sin 2x - \sqrt 3 \cos 2x = 2\cos x\]
\[ \Leftrightarrow \frac{1}{2}\sin 2x - \frac{{\sqrt 3 }}{2}\cos 2x = \cos x\]
\[ \Leftrightarrow \sin \frac{\pi }{6}.\sin 2{\rm{x}} - \cos \frac{\pi }{6}.\cos 2x = \cos x\]
\[ \Leftrightarrow - \cos \left( {2x + \frac{\pi }{6}} \right) = \cos x \Leftrightarrow \cos \left( {2x - \frac{{5\pi }}{6}} \right) = \cos x\]
\[ \Leftrightarrow \left[ \begin{array}{l}2x - \frac{{5\pi }}{6} = x + k2\pi \\2x - \frac{{5\pi }}{6} = - x + k2\pi \end{array} \right.,\,k \in \mathbb{Z} \Leftrightarrow \left[ \begin{array}{l}x = \frac{{5\pi }}{6} + k2\pi \\x = \frac{{5\pi }}{{18}} + k\frac{{2\pi }}{3}\end{array} \right.,\,\,k \in \mathbb{Z}\]
Kết hợp ĐKXĐ, suy ra: Phương trình đã cho có nghiệm \[x = \frac{{5\pi }}{{18}} + k\frac{{2\pi }}{3},\,\,k \in \mathbb{Z}\].
Câu 19:
 Xem đáp án
Xem đáp án
Phương pháp:
Áp dụng công thức khai triển nhị thức Newton: \[{\left( {x + y} \right)^n} = \sum\limits_{i = 0}^n {C_n^i{x^i}.{y^{n - i}}} \]
Cách giải:
Ta có: \[{\left( {\frac{x}{2} - 4m} \right)^{12}} = \sum\limits_{i = 0}^{12} {C_{12}^i{{\left( {\frac{1}{2}x} \right)}^i}.{{\left( { - 4m} \right)}^{12 - i}}} = \sum\limits_{i = 0}^{12} {C_{12}^i{{\left( { - 1} \right)}^{12 - i}}{2^{24 - 3i}}{m^{12 - i}}{x^i}} \]
Hệ số của các số hạng chứa \[{x^2}\], số hạng chứa \[{x^4}\], số hạng chứa \[{x^6}\] lần lượt là:
\[a = C_{12}^2{2^{18}}{m^{10}},\,\,b = C_{12}^4{2^{12}}{m^8},\,c = C_{12}^6{2^6}{m^4}\]
Theo đề bài:
\[a = bc \Leftrightarrow C_{12}^2{2^{18}}{m^{10}} = C_{12}^4{2^{12}}{m^8}.C_{12}^6{2^6}{m^4} \Leftrightarrow C_{12}^2{m^{10}} = C_{12}^4C_{12}^6{m^{12}} \Leftrightarrow {m^{10}}\left( {66 - 495.924{m^2}} \right) = 0\]
\[ \Leftrightarrow \left[ \begin{array}{l}m = 0\\{m^2} = \frac{1}{{6930}}\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}m = 0\\m = \pm \sqrt {\frac{1}{{6930}}} \end{array} \right.\]
Câu 20:
 Xem đáp án
Xem đáp án
Phương pháp:
Xác suất của biến cố A là: \(P\left( A \right) = \frac{{n\left( A \right)}}{{n\left( \Omega \right)}}\).
Cách giải:
Gọi số học sinh nam của trường là n (học sinh, \(n \in \mathbb{N}\))
Số phần tử của không gian mẫu: \(n\left( \Omega \right) = C_{n + 10}^5\)
Xác suất để cả 5 học sinh được chọn toàn nam: \(\frac{{C_n^5}}{{C_{n + 10}^5}}\).
Xác suất trong 5 học sinh được chọn có 2 nữ: \(\frac{{C_{10}^2C_n^3}}{{C_{n + 10}^5}}\).
Theo đề bài, ta có:
\(\frac{{C_n^5}}{{C_{n + 10}^5}} = \frac{7}{{15}}.\frac{{C_{10}^2C_n^3}}{{C_{n + 10}^5}} \Leftrightarrow 15C_n^5 = 7C_{10}^2C_n^3 \Leftrightarrow 15C_n^5 = 7.45C_n^3 \Leftrightarrow C_n^5 = 21C_n^3 \Leftrightarrow \frac{{n!}}{{5!\left( {n - 5} \right)!}} = \frac{{21.n!}}{{3!\left( {n - 3} \right)!}}\)
\( \Leftrightarrow \frac{{n!}}{{5!\left( {n - 5} \right)!}} = \frac{{21.n!}}{{3!\left( {n - 3} \right)!}} \Leftrightarrow 5.4 = \frac{{\left( {n - 3} \right)\left( {n - 4} \right)}}{{21}} \Leftrightarrow {n^2} - 7n + 12 - 420 = 0 \Leftrightarrow {n^2} - 7n - 408 = 0 \Leftrightarrow \left[ \begin{array}{l}n = 24\,\left( {TM} \right)\\n = - 17\,\left( L \right)\end{array} \right.\)\( \Rightarrow \) Số học sinh nam của lớp 11A là: 24 học sinh.
\( \Rightarrow \)Lớp 11A có tất cả số học sinh là: \(10 + 24 = 34\) (học sinh)
Câu 21:
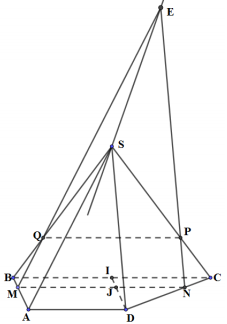
Cho hình chóp S.ABCD có đáy là hình thang ABCD với đáy lớn \(BC = 2{\rm{a}}\) và \(A{\rm{D}} = AB = a\). Mặt bên SAD là tam giác đều. Gọi M là điểm bất kì thuộc cạnh AB. Mặt phẳng \(\left( \alpha \right)\) đi qua M và song song với SA, BC, cắt CD, SC, SB lần lượt tại N, P, Q.
a) Chứng minh: \(PN//\left( {SA{\rm{D}}} \right)\).
b) Gọi E là giao điểm của MQ và NP. Chứng minh rằng E luôn nằm trên một đường thẳng cố định.
c) Giả sử \(AM = x\,\left( {0 < x < a} \right)\). Tính diện tích thiết diện tạo bởi mặt phẳng \(\left( \alpha \right)\) với hình chóp S.ABCD theo a và x. Tìm vị trí của M để thiết diện đạt giá trị lớn nhất?
 Xem đáp án
Xem đáp án
Phương pháp:
+) \(\left\{ \begin{array}{l}\left( P \right) \cap \left( Q \right) = d\\a \subset \left( P \right)\\a//\left( Q \right)\end{array} \right. \Rightarrow a//d\)
+) \(\left\{ \begin{array}{l}a,b \subset \left( P \right)\\a',\,b' \subset \left( Q \right)\\a//a',\,b//b'\\a \cap b = \left\{ I \right\}\end{array} \right. \Rightarrow \left( P \right)//\left( Q \right)\)
+) \(\left\{ \begin{array}{l}\left( P \right)//\left( Q \right)\\a \subset \left( P \right)\end{array} \right. \Rightarrow a//\left( Q \right)\)
Cách giải:
a) Ta có: \(\left\{ \begin{array}{l}\left( {MNPQ} \right) \cap \left( {SAB} \right) = MQ\\SA \subset \left( {SA{\rm{D}}} \right)\\SA//\left( {MNPQ} \right)\end{array} \right. \Rightarrow MQ//SA\) (1)
Do \(\left\{ \begin{array}{l}\left( {MNPQ} \right) \cap \left( {SBC} \right) = PQ\\BC \subset \left( {SBC} \right)\\BC//\left( {MNPQ} \right)\end{array} \right. \Rightarrow BC//PQ\). Mà \(A{\rm{D//BC}} \Rightarrow {\rm{PQ//AD}}\) (2)
Từ (1), (2) suy ra: \(\left( {MNPQ} \right)//\left( {SA{\rm{D}}} \right) \Rightarrow NP//\left( {SA{\rm{D}}} \right)\) (do \(NP \subset \left( {MNPQ} \right)\))
b) Ta có: \[E = MQ \cap NP\].
Mà \[MQ \subset \left( {SAB} \right),NP \subset \left( {SC{\rm{D}}} \right) \Rightarrow E \in \left( {SAB} \right) \cap \left( {SC{\rm{D}}} \right)\]
\[ \Rightarrow \] E luôn di động trên một đường thẳng cố định, chính là giao tuyến của (SAB) và (SCD).
c) Thiết diện của hình chóp cắt bởi \[\left( \alpha \right)\] là hình thang MNPQ (do \[MN//PQ\left( {//BC} \right)\])
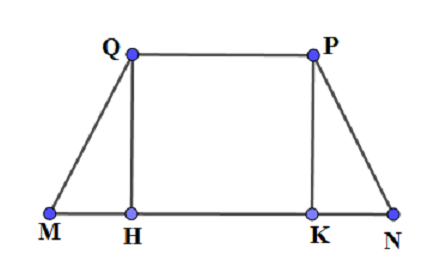
Ta có: \[\left\{ \begin{array}{l}MQ//SA\\MN//A{\rm{D}}\end{array} \right. \Rightarrow MQN = SA{\rm{D}} = 60^\circ \] (do tam giác SAD đều)
\[\left\{ \begin{array}{l}NP//S{\rm{D}}\\MN//A{\rm{D}}\end{array} \right. \Rightarrow QPN = S{\rm{D}}A = 60^\circ \] (do tam giác SAD đều)
\[ \Rightarrow MQN = QPN \Rightarrow \]MNPQ là hình thang cân.
+) \[MQ//SA \Rightarrow \frac{{AM}}{{AB}} = \frac{{MQ}}{{SA}} = \frac{{SQ}}{{SB}} = \frac{x}{a} \Rightarrow \left\{ \begin{array}{l}MQ = \frac{x}{a}.SA = \frac{x}{a}.a = x\\\frac{{SQ}}{{SB}} = \frac{x}{a}\end{array} \right.\]
+) \[PQ//BC \Rightarrow \frac{{PQ}}{{BC}} = \frac{{SQ}}{{SB}} = \frac{x}{a} \Rightarrow PQ = \frac{x}{a}.BC = \frac{x}{a}.2{\rm{a}} = 2{\rm{x}}\]
+) Gọi I là trung điểm của BC, J là giao điểm của ID và MN
Khi đó, ABID là hình thoi có các cạnh đều bằng a \[ \Rightarrow {\rm{MJ = a}}\] (do \[MJ//BI//A{\rm{D}}\])
\[JN//IC \Rightarrow \frac{{JN}}{{IC}} = \frac{{J{\rm{D}}}}{{I{\rm{D}}}} = \frac{{AM}}{{AB}} = \frac{x}{a} \Rightarrow JN = \frac{x}{a}.IC = \frac{x}{a}.a = x \Rightarrow MN = a + x\]
Gọi H, K lần lượt là hình chiếu của Q, P lên MN.
Do MNPQ là hình thang cân nên
\[MH = KN = \frac{{MN - PQ}}{2} = \frac{{x + a - 2{\rm{x}}}}{2} = \frac{{a - x}}{2}\]
\[\Delta MQH\] vuông tại H \[ \Rightarrow QH = MH.\tan 60^\circ = \frac{{a - x}}{2}.\sqrt 3 \]
Diện tích hình thang MNPQ là:
\[{S_{MNPQ}} = \frac{1}{2}\left( {PQ + MN} \right).QH = \frac{1}{2}.\left( {2{\rm{x}} + x + a} \right).\frac{{\sqrt 3 }}{2}\left( {a - x} \right)\]
\[ = \frac{{\sqrt 3 }}{{12}}\left( {3{\rm{x}} + a} \right)\left( {3{\rm{a}} - 3{\rm{x}}} \right)\]
Áp dụng BĐT Cô si, ta có: \[\left( {3{\rm{x}} + a} \right)\left( {3{\rm{a}} - 3{\rm{x}}} \right) \le {\left( {\frac{{3{\rm{x}} + a + 3{\rm{a}} - 3{\rm{x}}}}{2}} \right)^2} = 4{{\rm{a}}^2}\]
\[ \Rightarrow \frac{{\sqrt 3 }}{{12}}\left( {3{\rm{x}} + a} \right)\left( {3{\rm{a}} - 3{\rm{x}}} \right) \le \frac{{\sqrt 3 }}{{12}}.4{{\rm{a}}^2} = \frac{{{a^2}\sqrt 3 }}{3} \Rightarrow {S_{MNPQ}} \le \frac{{{a^2}\sqrt 3 }}{3}\]
Dấu “=” xảy ra khi và chỉ khi \[3{\rm{x}} + a = 3{\rm{a}} - 3{\rm{x}} \Leftrightarrow x = \frac{2}{3}a\]
Vậy, diện tích thiết diện MNPQ đạt giá trị lớn nhất \[\frac{{{a^2}\sqrt 3 }}{3}\] khi và chỉ khi M nằm trên cạnh AB sao cho \[AM = \frac{2}{3}a\].
Câu 22:
 Xem đáp án
Xem đáp án
Phương pháp:
Áp dụng: \[C_n^0 + C_n^1 + C_n^2 + ... + C_n^n = {2^n}\] và BĐT Cô si
Cách giải:
Ta có: \[C_n^0 + C_n^1 + C_n^2 + ... + C_n^n = {2^n} \Leftrightarrow C_n^1 + C_n^2 + ... + C_n^{n - 1} = {2^n} - 2\]
Áp dụng BĐT Cô si cho \[n - 1\] số dương \[C_n^1,\,C_n^2,\,...,\,C_n^{n - 1}\] ta có:
\[C_n^1 + C_n^2 + ... + C_n^{n - 1} \ge \left( {n - 1} \right)\sqrt[{n - 1}]{{C_n^1C_n^2\,...C_n^{n - 1}}},\,\forall n \in \mathbb{N},\,n \ge 2\]
\[ \Rightarrow {2^n} - 2 \ge \left( {n - 1} \right)\sqrt[{n - 1}]{{C_n^1C_n^2\,...C_n^{n - 1}}} \Leftrightarrow C_n^1C_n^2\,...C_n^{n - 1} \le {\left( {\frac{{{2^n} - 2}}{{n - 1}}} \right)^{n - 1}} \Leftrightarrow C_n^0C_n^1C_n^2\,...C_n^{n - 1}C_n^n \le {\left( {\frac{{{2^n} - 2}}{{n - 1}}} \right)^{n - 1}}\]
(do \[C_n^0 = C_n^n = 1\])
Vậy, \[C_n^0C_n^1C_n^2\,...C_n^n \le {\left( {\frac{{{2^n} - 2}}{{n - 1}}} \right)^{n - 1}},\,\forall n \in \mathbb{N},\,n \ge 2\].
