Bộ 20 đề thi học kì 1 Toán 11 năm 2022 - 2023 có đáp án
Bộ 20 đề thi học kì 1 Toán 11 năm 2022 - 2023 có đáp án (Đề 13)
-
876 lượt thi
-
18 câu hỏi
-
0 phút
Danh sách câu hỏi
Câu 1:
 Xem đáp án
Xem đáp án
Đáp án C
Phương pháp:
- Tính số phần tử của không gian mẫu.
- Liệt kê các khả năng có lợi cho biến cố.
- Tính xác suất \(P\left( A \right) = \frac{{n\left( A \right)}}{{n\left( \Omega \right)}}\).
Cách giải:
Gieo con xúc sắc hai lần, \(n\left( \Omega \right) = 6.6 = 36\).
Gọi A là biến cố: “Tổng số chấm xuất hiện trong hai lần gieo bằng 8”
Khi đó \(A = \left\{ {\left( {2;6} \right),\left( {3;5} \right),\left( {4;4} \right),\left( {5;3} \right),\left( {6;2} \right)} \right\} \Rightarrow n\left( A \right) = 5\)
Xác suất \(P\left( A \right) = \frac{5}{{36}}\).
Câu 2:
 Xem đáp án
Xem đáp án
Đáp án D
Phương pháp:
Dãy số \(\left( {{u_n}} \right)\) giảm nếu \(0 < \frac{{{u_{n + 1}}}}{{{u_n}}} < 1\) hoặc \({u_{n + 1}} - {u_n} < 0\).
Cách giải:
Đáp án A: \(\frac{{{u_{n + 1}}}}{{{u_n}}} < \frac{{{2^{n + 1}}}}{{{2^n}}} = 2 > 1\) nên dãy số tăng.
Đáp án B: \({u_{n + 1}} - {u_n} = 2\left( {n + 1} \right) - 5 - 2n + 5 = 2 > 0\) nên dãy số tăng.
Đáp án C: Dãy số \( - 3;9; - 27;81;...\) không tăng không giảm.
Đáp án D: \({u_{n + 1}} - {u_n} = \frac{{1 - \left( {n + 1} \right)}}{{3\left( {n + 1} \right) + 2}} - \frac{{1 - n}}{{3n + 2}} = \frac{{ - n}}{{3n + 5}} - \frac{{1 - n}}{{3n + 2}} = \frac{{ - 3{n^2} - 2n - 3n - 5 + 3{n^2} + 5n}}{{\left( {3n + 5} \right)\left( {3n + 2} \right)}}\)
\( = \frac{{ - 5}}{{\left( {3n + 5} \right)\left( {3n + 2} \right)}} < 0\)
Do đó dãy số \(\left( {{u_n}} \right)\) giảm.
Câu 3:
 Xem đáp án
Xem đáp án
Đáp án B
Phương pháp:
Nhận xét vị trí tương đối của đường thẳng a, b và kết luận.
Cách giải:
Nếu \(a//\left( \alpha \right)\), \(b \subset \left( \alpha \right)\) thì \(a//b\) hoặc a chéo b .
Câu 4:
 Xem đáp án
Xem đáp án
Đáp án D
Phương pháp:
Sử dụng lí thuyết về đường thẳng song song với mặt phẳng, hai mặt phẳng song song nhận xét tính đúng sai của từng đáp án.
Cách giải:
Đáp án A: sai, ta vẽ được vô số đường thẳng song song với mặt phẳng cho trước.
Đáp án B: sai, mọi đường thẳng nằm trong mặt phẳng này đều song song với mặt phẳng kia chứ không phải song song với mọi đường thẳng nằm trong mặt phẳng kia.
Đáp án C: sai, \(\left( \alpha \right)\) và \(\left( \beta \right)\) có thể cắt nhau theo giao tuyến song song với a và b.
Đáp án D: đúng.
Câu 5:
 Xem đáp án
Xem đáp án
Đáp án C
Phương pháp:
Muốn chứng minh một đường thẳng song song với một mặt phẳng, ta chỉ ra một đường thẳng nằm trong mặt này và song song với đường thẳng kia.
Cách giải:
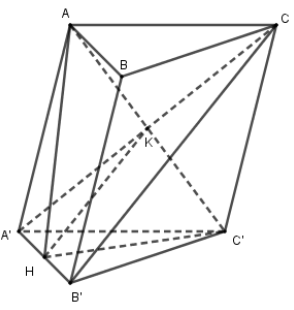
Gọi K là giao điểm của \(A'C\) và \(AC'\).
Tam giác \(A'B'C\) có HK là đường trung bình của tam giác nên \(HK//B'C\).
Mà \(HK \subset \left( {AHC'} \right)\) nên \(B'C//\left( {AHC'} \right)\).
Chú ý:
Các em có thể loại đáp án, chẳng hạn:
Đáp án A: \(B'C \subset \left( {HA'C} \right)\) nên A sai.
Đáp án B: \(B'C \cap \left( {HAB} \right) = B'\) nên B sai.
Đáp án D: \(B'C \cap \left( {AA'H} \right) = B'\) nên D sai.
Câu 6:
 Xem đáp án
Xem đáp án
Đáp án D
Phương pháp:
Giải phương trình \({u_n} = \frac{1}{3}\) tìm n.
Cách giải:
Ta có: \(\frac{{2n - 1}}{{5n + 3}} = \frac{1}{3} \Leftrightarrow 3\left( {2n - 1} \right) = 5n + 3 \Leftrightarrow n = 6\)
Câu 7:
 Xem đáp án
Xem đáp án
Đáp án B
Phương pháp:
Sử dụng công thức tính số hạng tổng quát \({T_{k + 1}} = C_n^k{a^{n - k}}{b^k}\)
Cách giải:
Số hạng tổng quát \({T_{k + 1}} = C_9^k{a^{9 - k}}{\left( {\frac{1}{{2x}}} \right)^k} = C_9^2.\frac{1}{{{2^k}}}.{x^{9 - 2k}}\).
Số hạng chứa \({x^3}\) ứng với \(9 - 2k = 3 \Leftrightarrow k = 3\).
Vậy số hạng chứa \({x^3}\) là \(C_9^3.\frac{1}{{{2^3}}}.{x^3} = \frac{1}{8}C_9^3{x^3}\)
Câu 8:
 Xem đáp án
Xem đáp án
Đáp án A
Phương pháp:
Sử dụng phương pháp loại đáp án, xét các đáp án đúng, từ đó suy ra đáp án sai.
Cách giải:
Đáp án B: Dễ thấy \(O{O_1}//DF \subset \left( {EFM} \right)\) nên B đúng.
Đáp án C: \(O{O_1}//CE \subset \left( {BEC} \right)\) nên C đúng.
Đáp án D: \(O{O_1}//DF \subset \left( {AFD} \right)\) nên D đúng.
Ngoài ra A sai vì \(M{O_1}//\left( {BEC} \right)\), thật vậy, \(O{O_1}//CE\), \(OM//BC\) nên \(\left( {O{O_1}M} \right)//\left( {BCE} \right) \Rightarrow M{O_1}//\left( {BCE} \right)\)
Câu 9:
 Xem đáp án
Xem đáp án
Đáp án C
Phương pháp:
Tính giá trị các số hạng của dãy và kết luận.
Cách giải:
Ta có: \({u_2} = \frac{1}{2}{u_1} + 1 = \frac{1}{2}.\left( { - 3} \right) + 1 = - \frac{1}{2}\)
\({u_3} = \frac{1}{2}{u_2} + 1 = \frac{1}{2}.\left( { - \frac{1}{2}} \right) + 1 = \frac{3}{4}\)
\({u_4} = \frac{1}{2}{u_3} + 1 = \frac{1}{2}.\frac{3}{4} + 1 = \frac{{11}}{8}\).
Câu 10:
 Xem đáp án
Xem đáp án
Đáp án B
Phương pháp:
Sử dụng công thức tính số hạng tổng quát \({T_{k + 1}} = C_n^k{a^{n - k}}{b^k}\)
Cách giải:
Số hạng tổng quát: \(C_{14}^k.{\left( {3{x^2}} \right)^{14 - k}}{\left( {\frac{1}{x}} \right)^k} = C_{14}^k{.3^{14 - k}}.{x^{28 - 2k}}.\frac{1}{{{x^k}}} = C_{14}^k{.3^{14 - k}}.{x^{28 - 3k}}\)
Số hạng chứa \({x^{10}}\) ứng với \(28 - 3k = 10 \Leftrightarrow k = 6\)
Hệ số \(C_{14}^6{.3^8}\).
Câu 11:
 Xem đáp án
Xem đáp án
Đáp án D
Phương pháp:
Thay \(n = 5\) vào công thức hàm số và tính toán.
Cách giải:
Ta có: \({u_5} = \frac{{{5^2} + 3}}{{{{2.5}^2} - 1}} = \frac{4}{7}\).
Câu 12:
 Xem đáp án
Xem đáp án
Đáp án B
Phương pháp:
- Tính số phần tử của không gian mẫu.
- Tính số các khả năng có lợi cho biến cố.
- Tính xác suất \(P\left( A \right) = \frac{{n\left( A \right)}}{{n\left( \Omega \right)}}\)
Cách giải:
Chọn 5 viên bi trong hộp có \(C_{15}^5 = 3003\) cách chọn hay \(n\left( \Omega \right) = 3003\).
Gọi A là biến cố “5 viên bi được chọn có đủ ba màu và số bi xanh bằng số bi vàng”
+ TH1: 1 xanh, 1 vàng và 3 đỏ, có \(C_6^1.C_5^1.C_4^3 = 120\) cách chọn.
+ TH2: 2 xanh, 2 vàng và 1 đỏ, có \(C_6^2.C_5^2.C_4^1 = 600\) cách chọn.
Do đó \(n\left( A \right) = 120 + 600 = 720\) cách chọn.
Xác suất \(P\left( A \right) = \frac{{n\left( A \right)}}{{n\left( \Omega \right)}} = \frac{{720}}{{3003}} = \frac{{240}}{{1001}}\).
Câu 13:
 Xem đáp án
Xem đáp án
Phương pháp:
1. Sử dụng công thức nhân đôi \(\sin 2x = 2\sin x\cos x\) đưa phương trình về dạng tích.
Cách giải:
1. Giải phương trình: \(\sin x + \sin 2x = 0\)
\(\sin x + \sin 2x = 0 \Leftrightarrow \sin x + 2\sin x\cos x = 0 \Leftrightarrow \sin x\left( {1 + 2\cos x} \right) = 0\)
\( \Leftrightarrow \left[ \begin{array}{l}\sin x = 0\\\cos x = - \frac{1}{2}\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = k\pi \\x = \pm \frac{2}{3} + k2\pi \end{array} \right.\), \(k \in \mathbb{Z}\)
Vậy phương trình có nghiệm \(x = k\pi \), \(x = \pm \frac{{2\pi }}{3} + k2\pi \), \(k \in \mathbb{Z}\).
Câu 14:
 Xem đáp án
Xem đáp án
Phương pháp:
2. Giải phương trình tìm n.
Sử dụng công thức tính số hạng tổng quát tìm số hạng chứa \({x^{29}}\).
Cách giải:
Ta có:
\(2C_n^2 - 19n = 0 \Leftrightarrow 2.\frac{{n\left( {n - 1} \right)}}{2} - 19n = 0 \Leftrightarrow {n^2} - n - 19n = 0 \Leftrightarrow {n^2} - 20n = 0 \Leftrightarrow \left[ \begin{array}{l}n = 0\left( {loai} \right)\\n = 20\left( {tm} \right)\end{array} \right.\)
Số hạng tổng quát \(C_{20}^k{\left( {{x^2}} \right)^{20 - k}}.{x^k} = C_{20}^k.{x^{40 - k}}\)
Số hạng chứa \({x^{29}}\) ứng với \(40 - k = 29 \Leftrightarrow k = 11\).
Vậy số hạng đó là \(C_{20}^{11}{x^{29}}\).
Câu 15:
1. Trong một nhóm học sinh khối 11 tham gia hoạt động thiện nguyện gồm 3 học sinh nữ và 7 học sinh nam. Cần chọn ra 5 học sinh tham gia trong đợt thứ nhất. Tính xác suất để 5 học sinh được chọn không có quá 1 học sinh nữ.
 Xem đáp án
Xem đáp án
Phương pháp:
1. - Tính số phần tử của không gian mẫu.
- Tính số các khả năng có lợi cho biến cố.
- Tính xác suất \(P\left( A \right) = \frac{{n\left( A \right)}}{{n\left( \Omega \right)}}\).
Cách giải:
1. Trong một nhóm học sinh khối 11 tham gia hoạt động thiện nguyện gồm 3 học sinh nữ và 7 học sinh nam. Cần chọn ra 5 học sinh tham gia trong đợt thứ nhất. Tính xác suất để 5 học sinh được chọn
không có quá 1 học sinh nữ.
Chọn 5 học sinh trong 10 học sinh, \(n\left( \Omega \right) = C_{10}^5 = 252\).
Gọi A là biến cố: “Chọn được không quá một học sinh nữ”.
+ TH1: Có 1 học sinh nữ và 4 học sinh nam có \(C_3^1.C_7^4 = 105\) cách.
+ TH2: Có 0 học sinh nữ và 5 học sinh nam có \(C_3^0.C_7^5 = 21\) cách.
Do đó \(n\left( A \right) = 105 + 21 = 126\).
Xác suất \(P\left( A \right) = \frac{{n\left( A \right)}}{{n\left( \Omega \right)}} = \frac{{126}}{{252}} = \frac{1}{2}\).Câu 16:
 Xem đáp án
Xem đáp án
Phương pháp:
2. Sử dụng qui tắc nhân xác suất và xác suất của biến cố đối.
Cách giải:
2. Trong trận bóng đá chung kết, hai bạn Việt và Nam tham gia sút phạt, biết rằng khả năng sút phạt vào lưới của Việt và Nam lần lượt là 0,7 và 0,8. Tính xác suất để ít nhất một bạn ghi bàn.
Gọi A là biến cố: “Ít nhất một bạn ghi bàn”
Khi đó \(\bar A\) là biến cố: “Không có bạn nào ghi bàn”
Xác suất để Việt không ghi bàn là: \(1 - 0,7 = 0,3\).
Xác suất để Nam không ghi bàn là: \(1 - 0,8 = 0,2\).
Xác suất để cả hai bạn không ghi bàn là: \(P\left( {\bar A} \right) = 0,3.0,2 = 0,06\).
Xác suất để ít nhất một bạn ghi bàn là: \(P\left( A \right) = 1 - P\left( {\bar A} \right) = 1 - 0,06 = 0,94\).
Câu 17:
Cho hình chóp S.ABCD có đáy là hình bình hành ABCD với O là giao điểm hai đường chéo AC và BD. Gọi M, N lần lượt là trung điểm các cạnh SA và SD.
1. Chứng minh MO song song với mặt phẳng \(\left( {SBC} \right)\) và mặt phẳng \(\left( {OMN} \right)\) song song với mặt phẳng \(\left( {SBC} \right)\).
2. Gọi K là trung điểm của MO. Chứng minh rằng NK song song với \(\left( {SBC} \right)\).
3. Xác định thiết diện của hình chóp S.ABCD cắt bởi mặt phẳng \(\left( {OMN} \right)\). Hỏi thiết diện là hình gì?
 Xem đáp án
Xem đáp án
Phương pháp:
1. Sử dụng định lí \(\left\{ \begin{array}{l}d \not\subset \left( P \right)\\a \subset \left( P \right)\\d//a\end{array} \right. \Rightarrow d//\left( P \right)\) để chứng minh đường thẳng song song mặt phẳng.
Sử dụng định lí \(\left\{ \begin{array}{l}a,b \subset \left( P \right),a'b' \subset \left( Q \right)\\a \cap b = I,a' \cap b' = I'\\a//a',b//b'\end{array} \right. \Rightarrow \left( P \right)//\left( Q \right)\) để chứng minh hai mặt phẳng song song.
2. Sử dụng định lí \(\left\{ \begin{array}{l}d \subset \left( P \right)\\\left( P \right)//\left( Q \right)\end{array} \right. \Rightarrow d//\left( Q \right)\) để chứng minh đường thẳng song song mặt phẳng.
3. Xác định các giao tuyến của mặt phẳng đã cho với các mặt của hình chóp và suy ra thiết diện.
Cách giải:
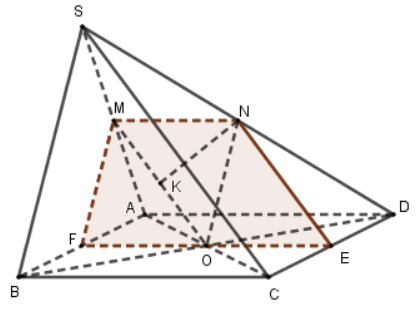
1. Chứng minh MO song song với mặt phẳng \(\left( {SBC} \right)\) và mặt phẳng \(\left( {OMN} \right)\) song song với mặt phẳng \(\left( {SBC} \right)\).
Ta có: MO là đường trung bình của tam giác SAC nên \(MO//SC\).
Mà \(SC \subset \left( {SBC} \right)\) nên \(MO//\left( {SBC} \right)\).
MN là đường trung bình của \(\Delta SAD\) nên \(MN//AD\), mà \(AD//BC\) nên \(MN//BC\).
Ta có: \(\left\{ \begin{array}{l}MN,MO \subset \left( {OMN} \right)\\BC,SC \subset \left( {SBC} \right)\end{array} \right. \Rightarrow \left( {OMN} \right)//\left( {SBC} \right)\)
2. Gọi K là trung điểm của MO. Chứng minh rằng NK song song với \(\left( {SBC} \right)\).
Dễ thấy \(NK \subset \left( {OMN} \right)\).
Mà \(\left( {OMN} \right)//\left( {SBC} \right)\) nên \(NK//\left( {SBC} \right)\).
3. Xác định thiết diện của hình chóp S.ABCD cắt bởi mặt phẳng \(\left( {OMN} \right)\). Hỏi thiết diện là hình gì?
Ta có:
\(BC \subset \left( {SBC} \right)//\left( {OMN} \right)\) nên \(BC//\left( {OMN} \right)\)
Mà \(BC \subset \left( {ABCD} \right)\) nên \(\left( {OMN} \right) \cap \left( {ABCD} \right) = Ox//BC\).
Trong \(\left( {ABCD} \right)\), qua O kẻ đường thẳng song song với BC cắt CD, AB lần lượt tại E, F.
Khi đó,
\(\left( {OMN} \right) \cap \left( {ABCD} \right) = EF\)
\(\left( {OMN} \right) \cap \left( {SAB} \right) = FM\)
\[\left( {OMN} \right) \cap \left( {SAD} \right) = MN\]
\[\left( {OMN} \right) \cap \left( {SCD} \right) = NE\]
\( \Rightarrow \) Thiết diện là tứ giác MNEF.
Mà \(MN//BC\), \(EF//BC\) nên \(MN//EF\) hay thiết diện là hình thang MNEF.
Câu 18:
 Xem đáp án
Xem đáp án
Phương pháp:
Gọi N là trung điểm của \(A'B'\), G là giao điểm của \(NC'\) với EF.
Từ đó mở rộng mặt phẳng \(\left( {FOE} \right)\) rồi tìm giao tuyến của \(\left( {FOE} \right)\) với các mặt của hình hộp.
Cách giải:
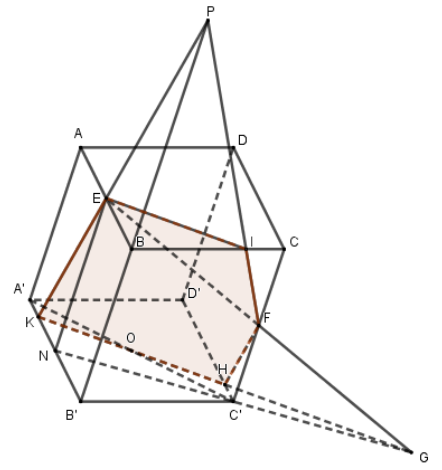
Gọi N là trung điểm của \(A'B' \Rightarrow NE//FC'\) nên bốn điểm N, E, F, C đồng phẳng.
Trong \(\left( {NEFC} \right)\), gọi \(G = NC' \cap EF \Rightarrow G \in EF \subset \left( {FOE} \right)\).
Trong \(\left( {A'B'C'D'} \right)\), gọi H, K lần lượt là giao điểm của GO với \(D'C'\), \(A'B'\)
Khi đó \(\left( {FOE} \right) \equiv \left( {GKE} \right)\).
Trong \(\left( {ABB'A'} \right)\), gọi \(P = KE \cap B'B \Rightarrow P \in BB' \subset \left( {BCC'B'} \right)\).
Trong \(\left( {BCC'B'} \right)\), gọi \(I = PF \cap BC \Rightarrow \left\{ \begin{array}{l}I \in BC\\I \in PF \subset \left( {GKE} \right) \equiv \left( {FOE} \right)\end{array} \right. \Rightarrow I = BC \cap \left( {FOE} \right)\).
Khi đó
\(\left( {FOE} \right) \cap \left( {A'B'C'D'} \right) = HK\)
\(\left( {FOE} \right) \cap \left( {ABB'A'} \right) = KE\)
\(\left( {FOE} \right) \cap \left( {ABCD} \right) = EI\)
\(\left( {FOE} \right) \cap \left( {BCC'B'} \right) = IF\)
\(\left( {FOE} \right) \cap \left( {DCC'D'} \right) = FH\)
Thiết diện là ngũ giác EIFHK.
Ta có, \(\frac{{IB}}{{IC}} = \frac{{PB}}{{CF}}\), \(CF = \frac{1}{2}CC' \Rightarrow \frac{{PB}}{{CF}} = \frac{{PB}}{{\frac{1}{2}CC'}} = 2.\frac{{PB}}{{BB'}}\) .
\(HC'//KN \Rightarrow \frac{{HC'}}{{KN}} = \frac{{GC'}}{{GN}}\)
Mà \(C'F//NE \Rightarrow \frac{{GC'}}{{GN}} = \frac{{C'F}}{{NE}} = \frac{1}{2} \Rightarrow \frac{{HC'}}{{KN}} = \frac{1}{2} \Rightarrow \frac{{A'K}}{{KN}} = \frac{1}{2} \Rightarrow \frac{{A'K}}{{A'N}} = \frac{1}{3} \Rightarrow \frac{{A'K}}{{A'B'}} = \frac{1}{6}\)
\( \Rightarrow \frac{{KN}}{{A'N}} = \frac{2}{3} = \frac{{K'N}}{{NB'}} \Rightarrow \frac{{K'N}}{{NB'}} = \frac{2}{5} \Rightarrow \frac{{NE}}{{PB'}} = \frac{2}{5} \Rightarrow \frac{{BB'}}{{PB'}} = \frac{2}{5} \Rightarrow \frac{{PB}}{{PB'}} = \frac{3}{5} \Rightarrow \frac{{PB}}{{BB'}} = \frac{3}{2}\)
Vậy \(\frac{{IB}}{{IC}} = \frac{{PB}}{{CF}} = 2.\frac{{PB}}{{BB'}} = 2.\frac{3}{2} = 3\).
