Bộ 20 đề thi học kì 1 Toán 11 năm 2022 - 2023 có đáp án
Bộ 20 đề thi học kì 1 Toán 11 năm 2022 - 2023 có đáp án (Đề 14)
-
863 lượt thi
-
10 câu hỏi
-
0 phút
Danh sách câu hỏi
Câu 1:
 Xem đáp án
Xem đáp án
Phương pháp:
Sử dụng công thức hạ bậc \[{\sin ^2}\alpha = \frac{{1 - \cos 2\alpha }}{2};{\rm{ }}{\cos ^2}\alpha = \frac{{1 + \cos 2\alpha }}{2}\]
Cách giải:
\[{\sin ^2}\left( {\frac{x}{2}} \right) - 2{\cos ^2}\left( {\frac{x}{4}} \right) + \frac{3}{4} = 0\]
\[ \Leftrightarrow \frac{{1 - \cos x}}{2} - 2.\frac{{1 + \cos \frac{x}{2}}}{2} + \frac{3}{4} = 0 \Leftrightarrow 2 - 2\cos x - 4 - 4\cos \frac{x}{2} + 3 = 0\]
\[ \Leftrightarrow \left( {2\cos x - 1} \right) + 4\cos \frac{x}{2} = 0 \Leftrightarrow {\cos ^2}\frac{x}{2} + 4\cos \frac{x}{2} = 0 \Leftrightarrow \cos \frac{x}{2}\left( {\cos \frac{x}{2} + 4} \right) = 0\]
\[ \Leftrightarrow \left[ \begin{array}{l}\cos \frac{x}{2} = 0\\\cos \frac{x}{2} + 4 = 0\left( {VN} \right)\end{array} \right. \Leftrightarrow \frac{x}{2} = \frac{\pi }{2} + k\pi \Leftrightarrow x = \pi + k2\pi \]
Vậy phương trình có nghiệm \[x = \pi + k2\pi ,{\rm{ }}k \in \mathbb{Z}\].
Câu 2:
 Xem đáp án
Xem đáp án
Phương pháp:
Sử dụng công thức tính số hạng tổng quát \[{T_{k + 1}} = C_n^k{a^{n - k}}{b^k}\].
Cách giải:
Số hạng tổng quát: \[{T_{k + 1}} = C_5^k.{\left( {3{x^3}} \right)^{5 - k}}.{\left( { - \frac{2}{{{x^2}}}} \right)^k} = C_5^k{.3^{5 - k}}.{x^{15 - 3k}}.\frac{{{{\left( { - 2} \right)}^k}}}{{{x^{2k}}}} = C_5^k{.3^{5 - k}}.{\left( { - 2} \right)^k}.{x^{15 - 5k}}\]
Số hạng không chứa \[x\] ứng với \[15 - 5k = 0 \Leftrightarrow k = 3\]
Vậy số không chứa \[x\] là: \[C_5^3{.3^{5 - 3}}.{\left( { - 2} \right)^3} = - 720\].
Câu 3:
Cho cấp số cộng \[\left( {{u_n}} \right)\] là một dãy số tăng thỏa mãn điều kiện \[\left\{ \begin{array}{l}{u_{31}} + {u_{34}} = 11\\u_{31}^2 + u_{34}^2 = 101\end{array} \right.\].
Tìm số hạng đầu tiên \[{u_1}\], công sai \[d\] và số hạng tổng quát của cấp số cộng đó.
 Xem đáp án
Xem đáp án
Phương pháp:
Sử dụng công thức: \[{u_n} = {u_1} + \left( {n - 1} \right)d\].
Cách giải:
Ta có: \[\left\{ \begin{array}{l}{u_{31}} + {u_{34}} = 11\\u_{31}^2 + u_{34}^2 = 101\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{u_{34}} = 11 - {u_{31}}\\u_{31}^2 + {\left( {11 - {u_{31}}} \right)^2} = 101\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{u_{34}} = 11 - {u_{31}}\\2u_{31}^2 - 22{u_{31}} + 121 = 101\end{array} \right.\]
\[ \Leftrightarrow \left\{ \begin{array}{l}{u_{34}} = 11 - {u_{31}}\\2u_{31}^2 - 22{u_{31}} + 20 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{u_{34}} = 11 - {u_{31}}\\{u_{31}} = 2,{u_{31}} = 10\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}{u_{31}} = 2,{u_{34}} = 9\\{u_{31}} = 10,{u_{34}} = 1\end{array} \right.\]
Mà dãy \[\left( {{u_n}} \right)\] tăng nên \[{u_{34}} > {u_{31}}\], do đó \[{u_{31}} = 2,{\rm{ }}{u_{34}} = 9\]
\[ \Rightarrow \left\{ \begin{array}{l}{u_1} + 30d = 2\\{u_1} + 33d = 9\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}d = \frac{7}{3}\\{u_1} = - 68\end{array} \right.\]
Số hạng tổng quát \[{u_n} = - 68 + \frac{7}{3}\left( {n - 1} \right)\].
Vậy \[{u_1} = - 68,{\rm{ }}d = \frac{7}{3},{\rm{ }}{u_n} = - 68 + \frac{7}{3}\left( {n - 1} \right)\].
Câu 4:
 Xem đáp án
Xem đáp án
Phương pháp:
- Tính số phần tử không gian mẫu \[n\left( \Omega \right)\]
- Tính số khả năng có lợi cho biến cố \[A\] đã cho.
- Tính xác suất \[P\left( A \right) = \frac{{n\left( A \right)}}{{n\left( \Omega \right)}}\].
Cách giải:
Chọn 4 trong 16 quả cầu, \[n\left( \Omega \right) = C_{16}^4 = 1820\].
Gọi \[A\] là biến cố: “Có đúng 1 quả cầu đỏ và không quá 2 quả cầu vàng”
TH1: Chọn được 1 quả cầu đỏ, 2 quả cầu vàng, 1 quả cầu xanh có \[C_4^1.C_7^2.C_5^1 = 420\] cách.
TH2: Chọn được 1 quả cầu đỏ, 1 quả cầu vàng, 2 quả cầu xanh có \[C_4^1.C_7^1.C_5^2 = 280\] cách.
TH3: Chọn được 1 quả cầu đỏ, 0 quả cầu vàng, 3 quả cầu xanh có \[C_4^1.C_7^0.C_5^3 = 40\] cách.
Do đó \[n\left( A \right) = 420 + 280 + 40 = 740\].
Xác suất \[P\left( A \right) = \frac{{n\left( A \right)}}{{n\left( \Omega \right)}} = \frac{{740}}{{1820}} = \frac{{37}}{{91}}\].
Câu 5:
 Xem đáp án
Xem đáp án
Phương pháp:
- Tìm CSC đã cho bằng cách sử dụng công thức \[{S_n} = \frac{{n\left[ {2{u_1} + \left( {n - 1} \right)d} \right]}}{2}\]
- Thay vào tổng đã cho tính toán.
Cách giải:
Ta có: \[24850 = {S_{100}} = \frac{{100\left( {2.1 + 99d} \right)}}{2} \Leftrightarrow d = 5\]
Khi đó \[{u_1} = 1,{\rm{ }}{u_2} = 6,{\rm{ }}{u_3} = 11,{\rm{ }}{u_4} = 16,...,{u_{49}} = {u_1} + 48d = 241,{\rm{ }}{u_{50}} = {u_1} + 49d = 246\]
\[ \Rightarrow S = \frac{1}{{{u_1}{u_2}}} + \frac{1}{{{u_2}{u_3}}} + ... + \frac{1}{{{u_{49}}{u_{50}}}} = \frac{1}{{1.6}} + \frac{1}{{6.11}} + \frac{1}{{11.16}} + ... + \frac{1}{{241.246}}\] \[ = \frac{1}{5}\left( {\frac{1}{1} - \frac{1}{6}} \right) + \frac{1}{5}\left( {\frac{1}{6} - \frac{1}{{11}}} \right) + ... + \frac{1}{5}\left( {\frac{1}{{241}} - \frac{1}{{246}}} \right)\]
\[ = \frac{1}{5}\left( {1 - \frac{1}{6} + \frac{1}{6} - \frac{1}{{11}} + ... + \frac{1}{{241}} - \frac{1}{{246}}} \right)\]
\[ = \frac{1}{5}\left( {1 - \frac{1}{{246}}} \right) = \frac{{49}}{{246}}\]
Vậy \[S = \frac{{49}}{{246}}\].
Câu 6:
 Xem đáp án
Xem đáp án
Phương pháp:
a) Sử dụng định lí ba giao tuyến song song: \[\left\{ \begin{array}{l}\left( \alpha \right) \cap \left( \beta \right) = {d_1}\\\left( \beta \right) \cap \left( \gamma \right) = {d_2}\\\left( \alpha \right) \cap \left( \gamma \right) = {d_3}\\{d_1}//{d_2}\end{array} \right. \Rightarrow {d_3}//{d_1}//{d_2}\].
Cách giải:
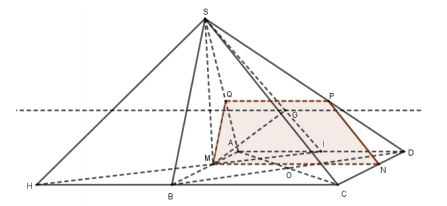
1) Tìm giao tuyến của mặt phẳng \[\left( {SAD} \right)\] và mặt phẳng \[\left( {GBC} \right)\]. Tìm giao điểm \[H\] của đường thẳng \[BC\] với mặt phẳng \[\left( {SGM} \right)\].
Dễ thấy \[G \in \left( {GBC} \right) \cap \left( {SAD} \right)\].
Xét các mặt phẳng: \[\left( {GBC} \right),{\rm{ }}\left( {SAD} \right),{\rm{ }}\left( {ABCD} \right)\] có:
\[\left\{ \begin{array}{l}\left( {GBC} \right) \cap \left( {SAD} \right) = Gx\\\left( {SAD} \right) \cap \left( {ABCD} \right) = AD\\\left( {ABCD} \right) \cap \left( {GBC} \right) = BC\\BC//AD\end{array} \right. \Rightarrow Gx//AB//CD\]
Vậy \[\left( {SAD} \right) \cap \left( {GBC} \right) = Gx\] là đường thẳng đi qua \[G\] và song song \[AD\].
Gọi \[I\] là trung điểm \[AD\], khi đó \[\left( {SGM} \right) \equiv \left( {SIM} \right)\].
Trong \[\left( {ABCD} \right)\], gọi \[H = IM \cap BC \Rightarrow \left\{ \begin{array}{l}H \in IM \subset \left( {SIM} \right)\\H \in BC\end{array} \right. \Rightarrow H = BC \cap \left( {SMG} \right)\].
Câu 7:
 Xem đáp án
Xem đáp án
Phương pháp:
b) Sử dụng định lí \[\left\{ \begin{array}{l}a \not\subset \left( P \right)\\a//b\\b \subset \left( P \right)\end{array} \right. \Rightarrow a//\left( P \right)\].
Cách giải:
2) Chứng minh rằng đường thẳng \[MG\] song song với mặt phẳng \[\left( {SBC} \right)\].
Vì \[AD//BC\] nên \[\frac{{MI}}{{MH}} = \frac{{MA}}{{MB}} = \frac{1}{2}\]
Xét tam giác \[SIH\] có \[\frac{{MI}}{{MH}} = \frac{{GI}}{{GS}} = \frac{1}{2}\] nên theo định lí Talet ta có \[MG//SH\].
Mà \[SH \subset \left( {SBC} \right)\] nên \[MG//\left( {SBC} \right)\].
Câu 8:
 Xem đáp án
Xem đáp án
Phương pháp:
c) Sử dụng hệ quả \[\left\{ \begin{array}{l}a//\left( P \right)\\a \subset \left( Q \right)\\\left( P \right) \cap \left( Q \right) = d\end{array} \right. \Rightarrow a//d\].
Cách giải:
3) Mặt phẳng \[\left( \alpha \right)\] đi qua \[M\] và song song với \[AD\] và \[SB\], \[\left( \alpha \right)\] cắt các cạnh \[CD,SD,SA\] lần lượt tại các điểm \[N,P,Q\]. Xác định thiết diện của mặt phẳng \[\left( \alpha \right)\] với hình chóp \[S.ABCD\].
Ta có: \[\left\{ \begin{array}{l}SB//\left( \alpha \right)\\SB \subset \left( {SAB} \right)\\\left( \alpha \right) \cap \left( {SAB} \right) = MQ\end{array} \right. \Rightarrow MQ//SB\]
Þ Trong \[\left( {SAB} \right)\], kẻ \[Mx//SB\] cắt \[SA\] tại \[Q\].
\[\left\{ \begin{array}{l}AD//\left( \alpha \right)\\AD \subset \left( {SAD} \right)\\\left( \alpha \right) \cap \left( {SAD} \right) = QP\end{array} \right. \Rightarrow QP//AD\]
Þ Trong \[\left( {SAD} \right)\], kẻ \[Qy//AD\] cắt \[SD\] tại \[P\].
\[\left\{ \begin{array}{l}AD//\left( \alpha \right)\\AD \subset \left( {ABCD} \right)\\\left( \alpha \right) \cap \left( {ABCD} \right) = MN\end{array} \right. \Rightarrow MN//AD\]
Þ Trong \[\left( {ABCD} \right)\], kẻ \[Mt//AD\] cắt \[CD\] tại \[N\].
Khi đó \[\left\{ \begin{array}{l}\left( \alpha \right) \cap \left( {SAB} \right) = MQ\\\left( \alpha \right) \cap \left( {SAD} \right) = QP\\\left( \alpha \right) \cap \left( {SCD} \right) = PN\\\left( \alpha \right) \cap \left( {ABCD} \right) = NM\end{array} \right.\] Þ Thiết diện là tứ giác \[MNPQ\].
Câu 9:
 Xem đáp án
Xem đáp án
Phương pháp:
- Sử dụng công thức cộng \[\sin a + \sin b = 2\sin \frac{{a + b}}{2}\cos \frac{{a - b}}{2}\] biến đổi phương trình về dạng tích.
- Giải phương trình và đối chiếu điều kiện, kết luận nghiệm.
Cách giải:
ĐK: \[\sin 3x \ne 0 \Leftrightarrow 3x \ne k\pi \Leftrightarrow x \ne \frac{{k\pi }}{3}\]
\[{\rm{PT}} \Rightarrow \sin x + \sin 2x = - \sin 3x \Leftrightarrow \left( {\sin x + \sin 3x} \right) + \sin 2x = 0\]
\[ \Leftrightarrow 2\sin 2x\cos x + \sin 2x = 0 \Leftrightarrow \sin 2x\left( {2\cos x + 1} \right) = 0\]
\[ \Leftrightarrow \left[ \begin{array}{l}\sin 2x = 0\\2\cos x + 1 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}\sin 2x = 0\\\cos x = - \frac{1}{2}\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}2x = k\pi \\x = \pm \frac{\pi }{3} + k2\pi \end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = \frac{{k\pi }}{2}\\x = \pm \frac{\pi }{3} + k2\pi \end{array} \right.,{\rm{ }}k \in \mathbb{Z}\]
Biểu diễn các nghiệm trên đường tròn lượng giác ta được:
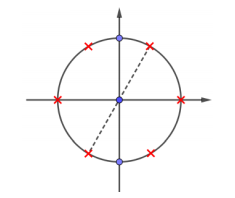
Quan sát hình vẽ ta thấy phương trình có nghiệm \[x = \frac{\pi }{2} + k\pi ,{\rm{ }}k \in \mathbb{Z}\] (hai điểm màu xanh).
Câu 10:
 Xem đáp án
Xem đáp án
Phương pháp:
- Đếm các số chẵn có 5 chữ số khác nhau mà có đúng hai chữ số lẻ.
- Đếm các số chẵn có 5 chữ số khác nhau mà có hai chữ số lẻ đứng cạnh nhau.
- Trừ các kết quả cho nhau ta được đáp số.
Cách giải:
Gọi số có năm chữ số có dạng \[\overline {abcde} \].
TH1: \[e = 0\] có 1 cách chọn.
Chọn 2 chữ số lẻ và 2 chữ số chẵn và xếp vị trí cho chúng có \[C_5^2.C_4^2.4!\] cách chọn.
Do đó có \[C_5^2.C_4^2.4!\] số.
TH2: \[e \in \left\{ {2;4;6;8} \right\}\] có 4 cách chọn.
+) Nếu \[a\] chẵn, \[a \ne 0,{\rm{ }}a \ne e\] thì có 3 cách chọn.
Số cách chọn 3 chữ số còn lại (1 chữ số chẵn và 2 chữ số lẻ) và xếp vị trí cho chúng là \[C_3^1.C_5^2.3!\] cách chọn.
Do đó có \[3.C_3^1.C_5^2.3!\] số.
+) Nếu \[a\] lẻ thì có 5 cách chọn.
Số cách chọn 3 chữ số còn lại (2 chữ số chẵn và 1 chữ số lẻ) và xếp vị trí cho chúng là \[C_4^2.C_4^1.3!\] cách chọn.
Do đó có \[5.C_4^2.C_4^1.3!\] số.
Khi đó số các số chẵn có 5 chữ số khác nhau mà chỉ có đúng 2 chữ số lẻ là
\[C_5^2.C_4^2.4! + 4.\left( {3.C_3^1.C_5^2.3! + 5.C_4^2.C_4^1.3!} \right) = 6480\] số.
Ta tính các số chẵn có 5 chữ số khác nhau chỉ có 2 chữ số lẻ mà chúng đứng cạnh nhau.
Coi hai chữ số lẻ đứng cạnh nhau là một chữ số \[A\], có \[A_5^2\] cách chọn và sắp xếp vị trí của hai chữ số trong \[A\].
Số có dạng \[\overline {abcd} \] với \[a,b,c,d \in \left\{ {A;0;2;4;6;8} \right\}\].
+) Nếu \[a = A\] thì có \[A_5^3\] cách chọn \[b,c,d\].
+) Nếu \[a \ne A,{\rm{ }}a \ne 0\] thì có 4 cách chọn.
\[A\] có thể đứng ở bị trí \[b\] hoặc \[c\] nên có 2 cách xếp.
Có \[A_4^2\] cách chọn và sắp xếp hai chữ số còn lại.
Do đó có \[A_5^2\left( {A_5^3 + 4.2.A_4^2} \right) = 3120\]
Vậy có \[6480 - 3120 = 3360\] số.
