Bộ 20 đề thi học kì 1 Toán 11 năm 2022 - 2023 có đáp án
Bộ 20 đề thi học kì 1 Toán 11 năm 2022 - 2023 có đáp án (Đề 2)
-
866 lượt thi
-
50 câu hỏi
-
0 phút
Danh sách câu hỏi
Câu 1:
 Xem đáp án
Xem đáp án
Đáp án A
Phương pháp:
Áp dụng tính chất giao tuyến của hai mặt phẳng có 1 điểm chung và 2 cạnh song song với nhau.
Cách giải:
Ta thấy \(\left( {SAD} \right)\); \(\left( {SBC} \right)\) có điểm chung thứ nhất là S.
Ta có: \(\left\{ \begin{array}{l}AD \subset \left( {SAD} \right)\\BC \subset \left( {SBC} \right)\\AD||BC\end{array} \right. \Rightarrow \) Giao tuyến của hai mặt phẳng là đường thẳng qua S và song song với AD, BC.
Câu 2:
 Xem đáp án
Xem đáp án
Đáp án D
Phương pháp:
Dựa vào tính chất của hàm số \(y = \cot x\).
Cách giải:
Hàm số \(y = \cot x\) là hàm số nghịch biến trên mỗi khoảng \(\left( {k\pi ;\pi + k\pi } \right)\), không phải đồ thị dạng hình sin.
Câu 3:
 Xem đáp án
Xem đáp án
Đáp án B
Phương pháp:
Sử dụng công thức \[\cos \left( {a - b} \right) = \cos a.\cos b + \sin a.\sin b\].
Cách giải:
Ta có
\(\sin x + \sqrt 3 \cos x = 2 \Leftrightarrow \frac{1}{2}\sin x + \frac{{\sqrt 3 }}{2}\cos x = 1\)
\( \Leftrightarrow \sin \frac{\pi }{6}.\sin x + \cos \frac{\pi }{6}.\cos x = 1 \Leftrightarrow \cos \left( {x - \frac{\pi }{6}} \right) = 1\)
\( \Leftrightarrow x - \frac{\pi }{6} = k2\pi \Leftrightarrow x = \frac{\pi }{6} + k2\pi \left( {k \in \mathbb{Z}} \right)\).
Câu 4:
 Xem đáp án
Xem đáp án
Đáp án D
Phương pháp:
Sử dụng công thức tính tổ hợp \(C_n^k = \frac{{n!}}{{k!.\left( {n - k} \right)!}}\)
Cách giải:
Cứ 2 điểm bất kì trong 2019 điểm đã cho sẽ tạo thành 2 véctơ khác véctơ không.
Do đó có tất cả số véctơ là: \(2.C_{2019}^2 = 2.\frac{{2019!}}{{2!.2017!}} = \frac{{2019!}}{{2017!}}\).
Câu 5:
 Xem đáp án
Xem đáp án
Đáp án C
Phương pháp:
Giải phương trình lượng giác đặc biệt: \(\sin x = - 1 \Leftrightarrow x = - \frac{\pi }{2} + k2\pi \left( {k \in \mathbb{Z}} \right)\).
Cách giải:
\(\sin \left( {2x - \frac{\pi }{6}} \right) + 1 = 0 \Leftrightarrow \sin \left( {2x - \frac{\pi }{6}} \right) = - 1\)
\( \Leftrightarrow 2x - \frac{\pi }{6} = \frac{{ - \pi }}{2} + k2\pi \Leftrightarrow x = - \frac{\pi }{6} + k\pi \left( {k \in \mathbb{Z}} \right)\).
Câu 6:
 Xem đáp án
Xem đáp án
Đáp án D
Phương pháp:
Sử dụng tổ hợp.
Cách giải:
Số cách chọn 3 đỉnh bất kì trong 12 đỉnh là \(\left| \Omega \right| = C_{12}^3\).
Để 3 đỉnh tạo thành 1 tam giác đều thì các đỉnh cách đều nhau. Do đó số cách chọn tam giác đều là \(\left| {{\Omega _A}} \right| = \frac{{12}}{3} = 4\).
Vậy xác suất là \[P = \frac{{\left| {{\Omega _A}} \right|}}{{\left| \Omega \right|}} = \frac{4}{{C_{12}^3}} = \frac{1}{{55}}\].
Câu 7:
 Xem đáp án
Xem đáp án
Đáp án B
Phương pháp:
Áp dụng định nghĩa của phép vị tự.
Cách giải:
\({V_{\left( {O;k} \right)}}\left( M \right) = M' \Leftrightarrow \overrightarrow {OM'} = k\overrightarrow {OM} \).
Câu 8:
 Xem đáp án
Xem đáp án
Đáp án D
Phương pháp:
Xác định ảnh của từng điểm qua phép tịnh tiến.
Cách giải:
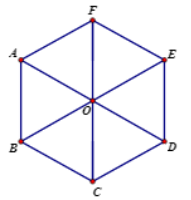
\({T_{\overrightarrow {BC} }}\left( A \right) = O\) do \(\overrightarrow {AO} = \overrightarrow {BC} \)
\({T_{\overrightarrow {BC} }}\left( B \right) = C\)
\({T_{\overrightarrow {BC} }}\left( O \right) = D\) do \(\overrightarrow {OD} = \overrightarrow {BC} \)
\({T_{\overrightarrow {BC} }}\left( F \right) = E\) do \(\overrightarrow {FE} = \overrightarrow {BC} \)
Vậy \({T_{\overrightarrow {BC} }}\left( {ABOF} \right) = OCDE\).
Câu 9:
 Xem đáp án
Xem đáp án
Đáp án D
Phương pháp:
Dựa vào hình vẽ trên.
Cách giải:
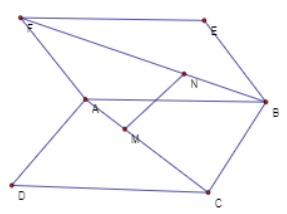
Trong mặt phẳng ADN ta kéo dài để \(MG \cap AN = K\)
Câu 10:
 Xem đáp án
Xem đáp án
Đáp án B
Phương pháp:
Chứng minh hai mặt phẳng song song rồi suy ra tính chất song song của đường thẳng và mặt phẳng.
Cách giải:
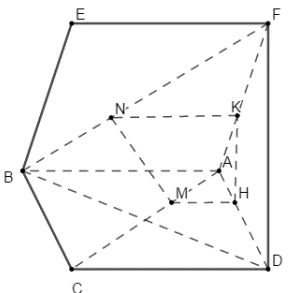
Lấy H, K lần lượt trên AD, AF sao cho \(\frac{{AH}}{{AP}} = \frac{{AK}}{{FA}} = \frac{{AM}}{{AC}} = \frac{{BN}}{{BF}}\)
Tam giác AFP có \(\frac{{AH}}{{AP}} = \frac{{AK}}{{FA}}\) áp dụng định lí Ta-lét đảo ta có \(HK||PF\).
Tương tự ta có \(KN||FE\)
Do đó \(\left( {HKN} \right)||\left( {DFE} \right) \Rightarrow \left( {MNKH} \right)||\left( {DFEC} \right) \Rightarrow MN||\left( {DCF} \right)\).
Câu 11:
 Xem đáp án
Xem đáp án
Đáp án B
Phương pháp:
Áp dụng tính chất hai đường thẳng song song trong không gian.
Cách giải:
Ta có \(a \subset \left( \alpha \right)\); \(b \subset \left( \beta \right)\) mà \(\left( \alpha \right)||\left( \beta \right)\).
Do đó 2 đường thẳng a, b có thể song song hoặc chéo nhau.
Câu 12:
 Xem đáp án
Xem đáp án
Đáp án B
Phương pháp:
Sử dụng tính chất song song.
Cách giải:
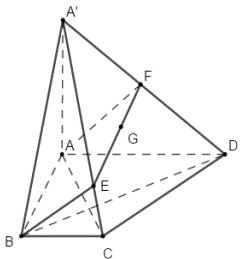
Từ G kẻ đường thẳng song song với AB lần lượt cắt SC, SD tại E, F.
Vậy thiết diện của hình chóp S.ABCD khi cắt bởi mặt phẳng \(\left( {ABG} \right)\) là hình tứ giác ABEF.
Câu 13:
 Xem đáp án
Xem đáp án
Đáp án A
Phương pháp:
Sử dụng tính chất của hàm số lượng giác.
Cách giải:
Ta có \(y = 1 + \sqrt 3 {\sin ^2}\left( {2x - \frac{\pi }{4}} \right)\). Mà \(0 \le {\sin ^2}\left( {2x - \frac{\pi }{4}} \right) \le 1\).
Do đó \(1 \le y \le 1 + \sqrt 3 \Rightarrow \left\{ \begin{array}{l}M = 1 + \sqrt 3 \\m = 1\end{array} \right.\)
Câu 14:
 Xem đáp án
Xem đáp án
Đáp án C
Phương pháp:
Sử dụng tính chất nhân.
Cách giải:
Số cách chọn nữ của tổ 1 là 7
Số cách chọn nữ của tổ 2 là 8
Do đó có \(7.8 = 56\) cách chọn 2 học sinh từ mỗi tổ đều là nữ.
Mặt khác số cách chọn 2 bạn (mỗi tổ 1 bạn) là \(13.13 = 169\)
Vậy xác suất là \(P = \frac{{56}}{{169}}\)
Câu 15:
 Xem đáp án
Xem đáp án
Đáp án A
Phương pháp:
Áp dụng tính chất của phép tịnh tiến điểm M thành \(M'\) theo vectơ v thì \(\overrightarrow {MM'} = \vec v\).
Cách giải:
Đường tròn \(\left( C \right)\): \({\left( {x - 1} \right)^2} + {\left( {y + 2} \right)^2} = 9\) có tâm \(I\left( {1; - 2} \right)\); bán kính \(R = 3\).
Gọi \(I'\) là tâm đường tròn \(\left( {C'} \right)\).
Phép tịnh tiến điểm I thành điểm \(I'\) theo véc-tơ \(\vec v\left( {3;3} \right)\) thì \(\overrightarrow {II'} = \vec v\)
Suy ra \(I'\left( {4;1} \right)\)
Đường tròn \(\left( {C'} \right)\) có tâm là \(I'\left( {4;1} \right)\); \(R = 3\) nên có dạng \({\left( {x - 4} \right)^2} + {\left( {y - 1} \right)^2} = 9\).
Câu 16:
 Xem đáp án
Xem đáp án
Đáp án A
Phương pháp:
Giải phương trình bậc hai rồi tìm nghiệm.
Cách giải:
\[3{\cos ^2}x + 2\cos x - 5 = 0 \Leftrightarrow \left( {3\cos x + 5} \right)\left( {\cos x - 1} \right) = 0\]
\[ \Leftrightarrow \left[ \begin{array}{l}\cos x = 1\\\cos x = - \frac{5}{3}\left( {loai} \right)\end{array} \right. \Leftrightarrow x = k2\pi \left( {k \in \mathbb{Z}} \right)\]
Câu 17:
 Xem đáp án
Xem đáp án
Đáp án D
Phương pháp:
Sử dụng tính chất song song trong không gian.
Cách giải:
Câu D sai vì hai đường thẳng phân biệt song song với cùng một mặt phẳng thì chúng song song hoặc chéo nhau.
Câu 18:
 Xem đáp án
Xem đáp án
Đáp án D
Phương pháp:
Xét các điều kiện có nghiệm của từng hàm số.
Cách giải:
+) phương trình \(\sqrt 3 \sin \left( {3x - \frac{\pi }{3}} \right) - 3 = 0 \Leftrightarrow \sin \left( {3x - \frac{\pi }{3}} \right) = \sqrt 3 > 1\) (Loại).
+) Phương trình \(\sin 3x + \sqrt 3 \cos 3x = - 4\) có nghiệm khi \({1^2} + 3 \ge {\left( { - 4} \right)^2}\)(vô lí).
+) Phương trình \(2\cos 3x + 3 = 0 \Leftrightarrow \cos 3x = - \frac{3}{2} < - 1\) (Loại).
Câu 19:
 Xem đáp án
Xem đáp án
Đáp án A
Phương pháp:
Đặt ẩn phụ rồi lập bảng xét dấu.
Cách giải:
Ta có \(y = \sqrt {8\cos x - 6\sin x - {{\left( {3\sin x - 4\cos x} \right)}^2} - 2m} \)
Hàm số trên có tập xác định R khi
\(8\cos x - 6\sin x - {\left( {3\sin x - 4\cos x} \right)^2} - 2m \ge 0\)
\( \Leftrightarrow 2\left( {4\cos x - 3\sin x} \right) - {\left( {3\sin x - 4\cos x} \right)^2} - 2m \ge 0\)
Đặt \(t = 4\cos x - 3\sin x\) có nghiệm khi \({t^2} \le 16 + 9 \Leftrightarrow - 5 \le t \le 5\)
Ta có bất phương trình \(2t - {t^2} - 2m \ge 0 \Leftrightarrow - 2m \ge {t^2} - 2t\) \(\left( 1 \right)\)
Đặt \(f\left( t \right) = {t^2} - 2t \Rightarrow f'\left( t \right) = 2t - 2 = 0 \Leftrightarrow t = 1\)
Bảng biến thiên:
|
t |
–5 |
|
1 |
|
5 |
|
\(f\left( t \right)\) |
35 |
 |
–1 |
 |
15 |
Dựa vào bảng biến thiên ta thấy bất đẳng thức \(\left( 1 \right)\) xảy ra khi \( - 2m \ge 35 \Leftrightarrow m \le - \frac{{35}}{2}\)
Câu 20:
 Xem đáp án
Xem đáp án
Đáp án C
Phương pháp:
Dựa vào tính chất đường trung bình của hình thang.
Cách giải:
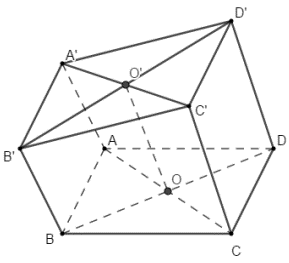
Do Ax, By, Cz, Dt song song với nhau cắt mặt phẳng \(\left( \alpha \right)\) lần lượt tại \(A'\), \(B'\), \(C'\), \(D'\)nên \(A'B'C'D'\) là hình bình hành và có tâm là \(O'\).
Gọi O là tâm hình bình hành ABCD.
Ta có \[OO'\] là đường trung bình của hình thang \[BDD'B'\], \(ACC'A'\).
\( \Rightarrow \frac{{A'A + CC'}}{2} = O'O = \frac{{BB' + D'D}}{2}\)
\( \Leftrightarrow A'A + CC' = BB' + D'D\)
\( \Leftrightarrow A'A = 5,2 + 7,8 - 8,6 = 4,4\,cm\)
Câu 21:
 Xem đáp án
Xem đáp án
Đáp án B
Phương pháp:
Sử dụng tổ hợp.
Cách giải:
+) Trong 6 học sinh có 5 học sinh nam, 1 học sinh nữ \( \Rightarrow \left| {{\Omega _A}} \right| = C_{20}^5.C_{15}^1\)
+) Cả 6 học sinh được chọn đều là nam \( \Rightarrow \left| {{\Omega _A}} \right| = C_{20}^6\)
Vậy tổng có \(C_{20}^6 + C_{20}^5.C_{15}^1 = 271320\)cách chọn thỏa mãn đề bài.
Câu 22:
 Xem đáp án
Xem đáp án
Đáp án D
Phương pháp:
Tính chất song song giữa 2 đường thẳng trong cùng một mặt phẳng.
Cách giải:
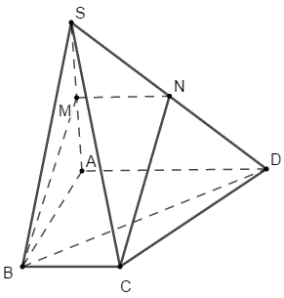
Từ M kẻ đường thẳng song song với BC cắt SD tại N \( \Rightarrow MN||BC\) hay \( \Rightarrow MN||BC\)
Mà M là trung điểm của SA nên N là trung điểm của SD.
Câu 23:
 Xem đáp án
Xem đáp án
Đáp án B
Phương pháp:
Áp dụng công thức của tổ hợp.
Cách giải:
Ta có \(C_n^k = \frac{{n!}}{{k!\left( {n - k} \right)!}}\)
Câu 24:
 Xem đáp án
Xem đáp án
Đáp án A
Phương pháp:
Hàm số lẻ là hàm số có dạng \(f\left( x \right) = - f\left( { - x} \right)\)
Hàm số chẵn là hàm số có dạng \(f\left( x \right) = f\left( { - x} \right)\)
Cách giải:
Ta có hàm số
\(y\left( x \right) = \sin x.{\cos ^2}x + \tan x\)
\( \Rightarrow y\left( { - x} \right) = \sin \left( { - x} \right).{\cos ^2}\left( { - x} \right) + \tan \left( { - x} \right)\)
\( \Leftrightarrow y\left( { - x} \right) = - \sin \left( x \right).{\cos ^2}\left( x \right) - \tan \left( x \right)\)
\( \Rightarrow y\left( x \right) = - y\left( { - x} \right)\)
Vậy đây là hàm số lẻ.
Câu 25:
 Xem đáp án
Xem đáp án
Đáp án A
Phương pháp:
Tìm 2 điểm chung của mặt phẳng.
Cách giải:
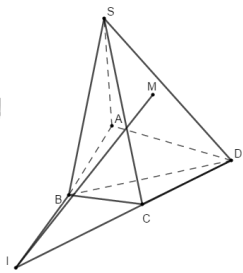
Trong mặt phẳng ABCD gọi \(I = AB \cap CD\)
Mặt phẳng \(\left( {AMB} \right)\), \(\left( {SCD} \right)\) có điểm chung là M và I.
Nên MI là giao điểm của 2 mặt phẳng trên.
Câu 26:
 Xem đáp án
Xem đáp án
Đáp án B
Phương pháp:
Áp dụng tính chất của phép vị tự.
Cách giải:
\(\left\{ \begin{array}{l}{V_{\left( {I; - 2} \right)}}\left( M \right) = M'\\{V_{\left( {I; - 2} \right)}}\left( N \right) = N'\end{array} \right. \Rightarrow M'N' = 2MN\)
\(M\left( {3; - 4} \right)\); \(N\left( {0; - 2} \right) \Rightarrow MN = \sqrt {13} \)
\( \Rightarrow M'N' = 2\sqrt {13} \)
Câu 27:
Phương trình \(3{\tan ^2}x + \left( {6 - \sqrt 3 } \right)\tan x - 2\sqrt 3 = 0\) có nghiệm là:
 Xem đáp án
Xem đáp án
Đáp án C
Phương pháp:
Giải phương trình bậc 2 rồi tìm nghiệm.
Cách giải:
Ta có \(3{\tan ^2}x + \left( {6 - \sqrt 3 } \right)\tan x - 2\sqrt 3 = 0\)
\( \Leftrightarrow \left[ \begin{array}{l}\tan x = \frac{{\sqrt 3 }}{3}\\\tan x = - 2\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = \frac{\pi }{6} + k\pi \\x = \arctan \left( { - 2} \right) + k\pi \end{array} \right.\left( {k \in \mathbb{Z}} \right)\)
Câu 28:
Cho hình chóp S.ABCD có đáy là hình bình hành. Gọi M, N, P lần lượt là trung điểm của AB, CD, SA (Tham khảo hình vẽ). Có bao nhiêu khẳng định đúng trong các khẳng định sau
i) \(\left( {MNP} \right)||\left( {SBC} \right)\). ii) \(NP||\left( {SBC} \right)\). 3i) \(MP||\left( {SCD} \right)\). 4i) \(MP||\left( {SBC} \right)\).
 Xem đáp án
Xem đáp án
Đáp án C
Phương pháp:
Dựa vào tính chất song song để chứng minh.
Cách giải:
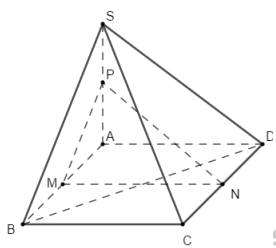
Ta có M, N, P lần lượt là trung điểm của AB, CD, SA.
Nên ta có \(\left\{ \begin{array}{l}MN||BC\\MP||SB\end{array} \right. \Rightarrow \left( {MNP} \right)||\left( {SBC} \right) \Rightarrow \left\{ \begin{array}{l}NP||\left( {SBC} \right)\\MP||\left( {SBC} \right)\end{array} \right.\)
Ta có \(MP||SB\); SB cắt \(\left( {SCD} \right)\) tại S nên MP không song song với \(\left( {SCD} \right)\).
Vậy mệnh đề đúng là I; II; IV
Câu 29:
 Xem đáp án
Xem đáp án
Đáp án B
Phương pháp:
Đưa 2 vế của phương trình về cùng dạng rồi suy ra x.
Cách giải:
Ta có \(\sqrt 3 \cot x + 3 = 0\)
\( \Leftrightarrow \cot x = - \sqrt 3 \Leftrightarrow x = \frac{{ - \pi }}{6} + k\pi \left( {k \in \mathbb{Z}} \right)\)
Câu 30:
Cho các mệnh đề sau:
\(\left( I \right)\): Hàm số \(y = \sin x\) có chu kì là \(\frac{\pi }{2}\).
\(\left( {II} \right)\): Hàm số \(y = \tan x\) có tập giá trị là \(\mathbb{R}\backslash \left\{ {\frac{\pi }{2} + k\pi |k \in \mathbb{Z}} \right\}\).
\(\left( {III} \right)\): Đồ thị hàm số \(y = \cos x\) đối xứng qua trục tung.
\(\left( {IV} \right)\): Hàm số \(y = \cot x\) đồng biến trên \(\left( { - \pi ;0} \right)\).
Có bao nhiêu mệnh đề đúng trong các mệnh đề trên?
 Xem đáp án
Xem đáp án
Đáp án A
Phương pháp:
Nhận xét từng mệnh đề rồi kết luận.
Cách giải:
Hàm số \(y = \sin x\) có chu kỳ là \(2\pi \) nên I sai.
Hàm số \(y = \tan x\) xác định khi \(\cos x \ne 0 \Leftrightarrow x \ne \frac{\pi }{2} + k\pi \left( {k \in \mathbb{Z}} \right)\) nên II đúng.
Ta có hàm số \(y = \cos x\) có \(y\left( x \right) = y\left( { - x} \right)\) nên đồ thị hàm số đối xứng với nhau qua trục tung nên III đúng.
Hàm số \(y = \cot x\) luôn nghịch biến trên R nên IV sai.
Câu 31:
 Xem đáp án
Xem đáp án
Đáp án C
Phương pháp:
Chứng minh đường thẳng đó song song với 1 cạnh thuộc mặt phẳng đó.
Cách giải:
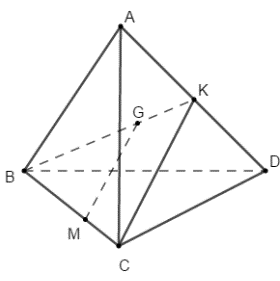
Gọi K là trung điểm của AD.
Tam giác ABD có trọng tâm G\( \Rightarrow \frac{{BG}}{{BK}} = \frac{2}{3}\)
Mà \(MB = 2MC \Rightarrow \frac{{MB}}{{BC}} = \frac{2}{3}\). Do đó \(\frac{{MB}}{{BC}} = \frac{{BG}}{{BK}} \Rightarrow MG||CK\)
Mà \(CK \subset \left( {ACD} \right) \Rightarrow MG||\left( {ACD} \right)\)
Câu 32:
 Xem đáp án
Xem đáp án
Đáp án B
Phương pháp:
Áp dụng tính chất:
Phương trình \[a\sin x + b\cos x = c\] có nghiệm khi \[{a^2} + {b^2} \ge {c^2}\].
Cách giải:
Ta có \( - \sqrt {2 - m} \sin x + \left( {m + 1} \right)\cos x = m - 1\) \(\left( * \right)\)
TXĐ: \(m \le 2\).
Áp dụng tính chất trên ta có: phương trình \(\left( * \right)\) có nghiệm khi
\(2 - m + {\left( {m + 1} \right)^2} \ge {\left( {m - 1} \right)^2} \Leftrightarrow m \ge \frac{2}{5}\)
Kết hợp điều kiện ta có \(\frac{2}{5} \le m \le 2\)
Câu 33:
 Xem đáp án
Xem đáp án
Đáp án A
Phương pháp:
Tìm điểm Q.
Sử dụng định lí Menelaus để tính tỉ số.
Cách giải:
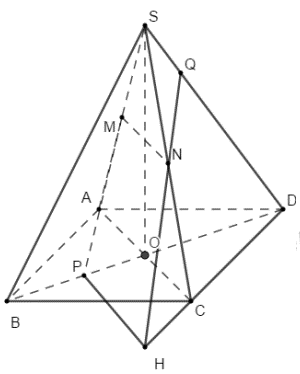
Trong \(\left( {ABCD} \right)\) lấy \(PH||MN\left( {H \in CD} \right)\)
Trong \(\left( {SCD} \right)\) gọi \(Q = NH \cap SD\)
Áp dụng định lí Menelaus trong tam giác SCD với cát tuyến QNH ta có: \(\frac{{HD}}{{HC}}.\frac{{NC}}{{NS}}.\frac{{QS}}{{QD}} = 1\)
Mà N là trung điểm của SC \( \Rightarrow \frac{{NC}}{{NS}} = 1\).
Mặt khác áp dụng định lí Ta-lét trong tam giác DPH ta có \(\frac{{HD}}{{HC}} = \frac{{DP}}{{OP}} = 3\) (vì P là trung điểm của OB).
Do đó ta có \(\frac{{QS}}{{QD}} = \frac{1}{3} \Rightarrow \frac{{SQ}}{{SD}} = \frac{1}{4}\)
Câu 34:
 Xem đáp án
Xem đáp án
Đáp án A
Phương pháp:
Sử dụng tổ hợp.
Cách giải:
Lấy 3 trong 20 điểm \({A_1}\), \({A_2}\), \({A_3}\), \({B_1}\), \({B_2}\), \({B_3}\), \({B_4}\), \({C_1}\), \({C_2}\),..., \({C_{13}}\) có số cách là \(C_{20}^3\) .
Mặt khác 3 điểm trong \({A_1}\), \({A_2}\), \({A_3}\)
\({B_1}\), \({B_2}\), \({B_3}\), \({B_4}\)
\({C_1}\), \({C_2}\),..., \({C_{13}}\)
thì sẽ không tạo thành một tam giác
Do đó số tam giác được tạo thành từ 20 điểm đã cho là \(C_{20}^3 - C_3^3 - C_4^3 - C_{13}^3 = 849\)
Câu 35:
 Xem đáp án
Xem đáp án
Đáp án D
Phương pháp:
Tìm điều kiện xác định của hàm số tan.
Tìm điều kiện xác định của hàm số khi mẫu khác không.
Cách giải:
Hàm số \(y = \frac{{2\sin x - 1}}{{\tan 2x + \sqrt 3 }}\) xác định khi
\(\left\{ \begin{array}{l}\cos 2x \ne 0\\\tan 2x \ne - \sqrt 3 \end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}2x \ne \frac{\pi }{2} + k\pi \\2x \ne \frac{{ - \pi }}{3} + k\pi \end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \ne \frac{\pi }{4} + k\frac{\pi }{2}\\x \ne \frac{\pi }{6} + k\frac{\pi }{2}\end{array} \right.\left( {k \in \mathbb{Z}} \right)\)
Câu 36:
 Xem đáp án
Xem đáp án
Đáp án C
Phương pháp:
Áp dụng tính chất nhân.
Cách giải:
Ta có số cách sắp xếp 5 cuốn sách toán khác nhau là 5!
Số cách sắp xếp 5 cuốn sách văn khác nhau là 5!
Có 2 cách để sắp xếp 5 cuốn sách toán khác nhau và 5 cuốn sách văn khác nhau thành 1 hàng ngang.
Do đó số cách xếp thỏa mãn bài toán là 2.5!.5!
Câu 37:
 Xem đáp án
Xem đáp án
Đáp án A
Phương pháp:
Áp dụng tính chất \(C_n^k = C_n^{n - k}\)
Áp dụng nhị thức Niu-tơn.
Cách giải:
Ta có \(\left\{ \begin{array}{l}C_{2n + 1}^1 = C_{2n + 1}^{2n}\\C_{2n + 1}^2 = C_{2n + 1}^{2n - 1}\\...\\C_{2n + 1}^n = C_{2n + 1}^{n + 1}\end{array} \right.\)
\( \Rightarrow A = C_{2n + 1}^1 + C_{2n + 1}^2 + ... + C_{2n + 1}^n = C_{2n + 1}^{n + 1} + C_{2n + 1}^{n + 2} + ... + C_{2n + 1}^{2n}\)
\( \Rightarrow A = \frac{{{2^{2n + 1}} - 2}}{2} = {2^{2n}} - 1\)
Theo giả thiết ta có \(A = {2^{24}} - 1 \Rightarrow n = 12\)
Khi đó \({\left( {{x^2} - x + \frac{1}{4}} \right)^2}{\left( {2x - 1} \right)^{24}} = {\left( {x - \frac{1}{2}} \right)^4}{\left( {2x - 1} \right)^{24}}\)
\( = \frac{{{{\left( {2x - 1} \right)}^{28}}}}{{16}} = \frac{1}{{16}}\sum\limits_{k \to 0}^{28} {C_{28}^k{{.2}^k}.{x^k}.{{\left( { - 1} \right)}^{28 - k}}} \)
Khi đó hệ số của \({x^9}\) hay \(k = 9\) là \( - C_{28}^9{.2^5}\)
Câu 38:
 Xem đáp án
Xem đáp án
Đáp án C
Phương pháp:
Sử dụng quy tắc nhân và quy tắc cộng.
Cách giải:
Gọi số cần tìm là \(\overline {abcd} \) \(\left( {a \ne 0} \right)\)
Để số cần tìm là số chẵn thì \(d \in \left\{ {0;2;4} \right\}\)
+) \(d = 0\) khi đó:
a có 5 cách chọn
b có 4 cách chọn
c có 3 cách chọn.
Khi đó có \(5.4.3 = 60\) số thỏa mãn.
+) \(d \in \left\{ {2;4} \right\}\) khi đó
a có 4 cách chọn
b có 4 cách chọn
c có 3 cách chọn.
khi đó có \(4.4.3.2 = 96\) số thỏa mãn.
Vậy có tất cả \(60 + 96 = 156\) số.
Câu 39:
 Xem đáp án
Xem đáp án
Đáp án B
Phương pháp:
Sử dụng quy tắc nhân.
Cách giải:
Xác suất sút 1 lần trúng là 0,7 nên xác suất sút 1 lần trượt là 0,3.
Mà 2 lần sút là độc lập nên có 2 cách sắp xếp để sút trượt và trúng trước hay sau.
Do đó xác suất là \[0,7.0,3.2 = 0,42\].
Câu 40:
 Xem đáp án
Xem đáp án
Đáp án A
Phương pháp:
Sử dụng quy tắc nhân và cộng.
Cách giải:
Ta có \(8 = 2 + 6 = 3 + 5 = 4 + 4\)
Xác suất 1 lần tung là \(\frac{1}{6}\)
Nên gieo xúc sắc 2 lần thì sẽ có xác suất là \({\left( {\frac{1}{6}} \right)^2} = \frac{1}{{36}}\)
Với lần tung \(\left\{ {2;6} \right\}\); \(\left\{ {3;4} \right\}\) sẽ có 2 cách sắp xếp xuất hiện.
Do đó xác suất để thỏa mãn bài toán là \(\frac{1}{{36}}.2 + \frac{1}{{36}}.2 + \frac{1}{{36}} = \frac{5}{{36}}\)
Câu 41:
 Xem đáp án
Xem đáp án
Đáp án B
Phương pháp:
Sử dụng tính chất của phép quay.
Cách giải:
Ta có \(\left( d \right)\): \(3x - y + 1 = 0\)
Gọi \(M\left( {0;1} \right) \in d\); Phép quay \({Q_{\left( {O; - 90^\circ } \right)}}\left( M \right) = M'\left( {a;b} \right)\)
\( \Rightarrow \overrightarrow {OM} \left( {0;1} \right)\); \(\overrightarrow {OM'} \left( {a;b} \right)\).
Phép quay \({Q_{\left( {O; - 90^\circ } \right)}}\left( d \right) = d'\) nên \(\left\{ \begin{array}{l}\overrightarrow {{n_d}} .\overrightarrow {{n_{d'}}} = 0\\OM' = OM = 1\\\overrightarrow {OM'} .\overrightarrow {OM} = 0\end{array} \right.\)
\( \Rightarrow \left\{ \begin{array}{l}\overrightarrow {{n_{d'}}} \left( {1; - 3} \right)\\{a^2} + {b^2} = 1\\b = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}\overrightarrow {{n_{d'}}} \left( {1; - 3} \right)\\b = 0\\a = 1\left( {do\,\,\alpha = 90^\circ } \right)\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}\overrightarrow {{n_{d'}}} \left( {1; - 3} \right)\\M'\left( {1;0} \right)\end{array} \right.\)
Khi đó phương trình đường thẳng \(\left( {d'} \right)\) là \(x + 3y - 1 = 0\)Câu 42:
 Xem đáp án
Xem đáp án
Đáp án C
Phương pháp:
Sử dụng tổ hợp.
Cách giải:
Tổng số bi xanh và trắng là \(7 + 6 = 13\).
Gọi A là biến cố: “Lấy 3 viên bi không có màu đỏ” \( \Rightarrow \left| {{\Omega _A}} \right| = C_{13}^3\)
Tổng số bi trong hộp là 16 \( \Rightarrow \left| \Omega \right| = C_{16}^3\)
Vậy \(P = \frac{{\left| {{\Omega _A}} \right|}}{{\left| \Omega \right|}} = \frac{{C_{13}^3}}{{C_{16}^3}} = \frac{{143}}{{280}}\)
Câu 43:
 Xem đáp án
Xem đáp án
Đáp án D
Phương pháp:
Sử dụng định lí Ta-lét đảo để chứng minh song song.
Cách giải:
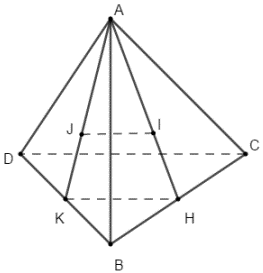
Gọi H, K lần lượt là trung điểm của BC, BD \( \Rightarrow HK||CD\); \(HK = \frac{1}{2}CD\) \(\left( 1 \right)\)
\(\Delta ABC\) có trọng tâm I, trung tuyến AH\( \Rightarrow \frac{{AI}}{{AH}} = \frac{2}{3}\)
Tương tự ta có \(\frac{{AJ}}{{AK}} = \frac{2}{3}\)
\( \Rightarrow \frac{{AI}}{{AH}} = \frac{{AJ}}{{AK}} \Rightarrow JI||HK\) (Định lí ta-lét đảo); \(JI = \frac{2}{3}HK\) \(\left( 2 \right)\)
Từ \(\left( 1 \right)\); \(\left( 2 \right)\) suy ra \(JI||CD\); \(JI = \frac{1}{3}CD\)
Câu 44:
 Xem đáp án
Xem đáp án
Đáp án D
Phương pháp:
Sử dụng tính chất nhị thức Niu-Tơn.
Cách giải:
+) Ta có \({\left( {1 + 2} \right)^n} = \sum\limits_{k \to 0}^n {C_n^k{{.2}^k}} = C_n^0 + 2C_n^1 + ... + {2^n}.C_n^n\)
Mà \(C_n^0 + 2C_n^1 + ... + {2^n}.C_n^n = 243\)
Nên \({3^n} = 243 \Leftrightarrow n = 5\)
+) Mặt khác \(C_{2m}^1 + C_{2m}^3 + ... + C_{2m}^{2m - 1} = 2048\).
\( \Leftrightarrow \frac{{{2^{2m}}}}{2} = 2048 \Leftrightarrow m = 6\)
Do đó \(m > n\).
Câu 45:
 Xem đáp án
Xem đáp án
Đáp án B
Phương pháp:
Sử dụng quy tắc nhân.
Cách giải:
Vì đồng xu có 2 mặt nên khi gieo 5 lần thì \({n_\Omega } = {2^5} = 32\)
Câu 46:
 Xem đáp án
Xem đáp án
Đáp án C
Phương pháp:
Áp dụng nhị thức Niu-tơn.
Cách giải:
\[P\left( x \right) = {\left( {x - 2y} \right)^5} = \sum\limits_{k \to 0}^5 {C_5^k.{x^{5 - k}}.{{\left( { - 2} \right)}^k}.{y^k}} \]
\[ \Leftrightarrow P\left( x \right) = {x^5} - 2C_5^1{x^4}.y + {2^2}C_5^2{x^3}.{y^2} - {2^3}C_5^3{x^2}.{y^3} + {2^4}C_5^4x.{y^4} - {2^5}C_5^5.{y^5}\]
Câu 47:
 Xem đáp án
Xem đáp án
Đáp án A
Phương pháp:
Áp dụng nhị thức Niu-tơn.
Cách giải:
Ta có:
\(S = C_{17}^0 - 3C_{17}^1 + 9C_{17}^2 - 27C_{17}^3 + ... - {3^{17}}C_{17}^{17}\)
\( \Leftrightarrow S = \sum\limits_{k \to 0}^{17} {C_{17}^k{{\left( { - 3} \right)}^k}} \)
Mặt khác \({\left( {1 - 3} \right)^{17}} = \sum\limits_{k \to 0}^{17} {C_{17}^k{{\left( { - 3} \right)}^k}} \)
Nên \(S = {\left( {1 - 3} \right)^{17}} = - {2^{17}}\)
Câu 48:
 Xem đáp án
Xem đáp án
Đáp án B
Phương pháp:
Đặt ẩn phụ, tìm nghiệm phương trình bậc 2 rồi tìm m.
Cách giải:
Ta có \[\left( {2m + 1} \right){\cos ^2}2x - \left( {3m - 1} \right)\sin 2x - 3m + 1 = 0\] \[\left( * \right)\].
Đặt \(t = \sin 2x \Rightarrow - 1 \le t \le 1\left( {x \in \left( { - \pi ;\pi } \right)} \right)\)
Khi đó phương trình \[\left( * \right)\] có dạng:
\[\left( {2m + 1} \right)\left( {1 - {t^2}} \right) - \left( {3m - 1} \right)t - 3m + 1 = 0\]
\[ \Leftrightarrow \left( {2m + 1} \right){t^2} + \left( {3m - 1} \right)t + m - 2 = 0\]
\[ \Leftrightarrow \left( {t + 1} \right)\left( {\left( {2m + 1} \right)t + m - 2} \right) = 0\]
\[ \Leftrightarrow \left[ \begin{array}{l}t = - 1\\\left( {2m + 1} \right)t + m - 2 = 0\end{array} \right.\]
Nếu: \(t = - 1\left( {tm} \right) \Rightarrow \sin 2x = - 1\)
\( \Leftrightarrow 2x = \frac{{ - \pi }}{2} + k2\pi \left( {k \in \mathbb{Z}} \right)\)
\( \Leftrightarrow x = \frac{{ - \pi }}{4} + k\pi \in \left( { - \pi ;\pi } \right)\)
\( \Rightarrow \frac{{ - 3}}{4} < k < \frac{5}{4} \Rightarrow k \in \left\{ {0;1} \right\}\)
Khi đó phương trình \[\left( * \right)\] có 2 nghiệm phân biệt là \(\frac{{ - \pi }}{4}\); \(\frac{{3\pi }}{4}\)
+) \(\left( {2m + 1} \right)t = 2 - m\) \(\left( 1 \right)\).
Nếu \(m = \frac{{ - 1}}{2}\); \(\left( 1 \right) \Rightarrow m = 2\left( {ktm} \right)\)
\( \Rightarrow m \ne \frac{{ - 1}}{2} \Rightarrow t = \frac{{2 - m}}{{2m + 1}}\)
Để phương trình \[\left( * \right)\] có 2 nghiệm phân biệt thì
\(\left[ \begin{array}{l}t = \frac{{2 - m}}{{2m + 1}} = - 1\\t < - 1\\t > 1\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}m = - 3\\\frac{{m + 3}}{{2m + 1}} < 0 \Leftrightarrow - 3 < m < \frac{{ - 1}}{2} \Leftrightarrow m \in \left\{ { - 2; - 1} \right\}\\\frac{{3m - 1}}{{2m + 1}} < 0 \Leftrightarrow \frac{{ - 1}}{2} < m < \frac{1}{3} \Leftrightarrow m = 0\end{array} \right.\)
Vậy có 4 giá trị của m thỏa mãn.Câu 49:
 Xem đáp án
Xem đáp án
Đáp án D
Phương pháp:
Áp dụng tính chất phép quay.
Cách giải:
Phép quay biến đường thẳng thành đường thẳng, biến đoạn thẳng thảnh đoạn thẳng bằng nó, biến tam giác thành tam giác bằng nó, biến đường tròn thành đường tròn có cùng bán kính với nó.
Câu 50:
 Xem đáp án
Xem đáp án
Đáp án A
Phương pháp:
Sử dụng tỉ số và định lí Ta-lét.
Cách giải:
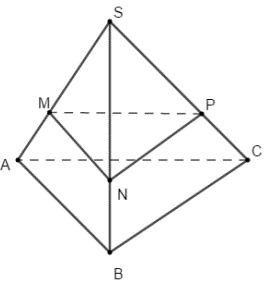
Gọi N, P lần lượt thuộc SB, SC sao cho \(\frac{{SN}}{{SB}} = \frac{{SP}}{{SC}} = \frac{{SM}}{{SA}}\).
Khi đó thiết diện của mặt phẳng qua M song song với \(\left( {ABC} \right)\) là tam giác MNP.
Áp dụng định lí ta-lét trong tam giác SAB có: \(\frac{{MN}}{{AB}} = \frac{{SM}}{{SA}} = \frac{2}{3} = 4\)\(\left( {SM = 2MA;SA = 6} \right)\)
Tương tự ta có \(NP = MP = 4\,cm\).
Do đó tam giác MNP là tam giác đều cạnh 4cm.
\( \Rightarrow {S_{MNP}} = \frac{{\sqrt 3 }}{4}{.4^2} = 4\sqrt 3 c{m^2}\)
