Câu hỏi:
03/04/2024 36
Cho hình chóp \[S.ABCD\] có đáy \[ABCD\] là hình bình hành. Gọi \[O\] là giao điểm của \[AC\] và \[BD\]. \[M\] và \[N\] lần lượt là trung điểm của \[CD\] và \[SA\]. \[G\] là trọng tâm tam giác \[SAB\].
1) Tìm giao tuyến của hai mặt phẳng \[\left( {SAC} \right)\] và \[\left( {SBD} \right)\].
2) Chứng minh \[MN\] song song với mặt phẳng \[\left( {SBC} \right)\].
3) Gọi \[\Delta \] là giao tuyến của hai mặt phẳng \[\left( {SAD} \right)\] và \[\left( {SMG} \right)\], \[P\] là giao điểm của đường thẳng \[OG\] và \[\Delta \]. Chứng minh \[P,N,D\] thẳng hàng.
Cho hình chóp \[S.ABCD\] có đáy \[ABCD\] là hình bình hành. Gọi \[O\] là giao điểm của \[AC\] và \[BD\]. \[M\] và \[N\] lần lượt là trung điểm của \[CD\] và \[SA\]. \[G\] là trọng tâm tam giác \[SAB\].
1) Tìm giao tuyến của hai mặt phẳng \[\left( {SAC} \right)\] và \[\left( {SBD} \right)\].
2) Chứng minh \[MN\] song song với mặt phẳng \[\left( {SBC} \right)\].
3) Gọi \[\Delta \] là giao tuyến của hai mặt phẳng \[\left( {SAD} \right)\] và \[\left( {SMG} \right)\], \[P\] là giao điểm của đường thẳng \[OG\] và \[\Delta \]. Chứng minh \[P,N,D\] thẳng hàng.
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Phương pháp:
1) Xác định hai điểm chung của hai mặt phẳng.
2) + Gọi \[Q\] là trung điểm của \[SB\].
+ Chứng minh \[MN\] song song với một đường thẳng bất kì chứa trong \[\left( {SBC} \right)\].
3) + Xác định \[\Delta \].
+ Xác định giao tuyến của \[\left( {SAD} \right)\] và \[\left( {BDG} \right)\].
+ Chứng minh \[P\] là điểm chung của hai mặt phẳng \[\left( {SAD} \right)\] và \[\left( {BDG} \right)\].
Cách giải:
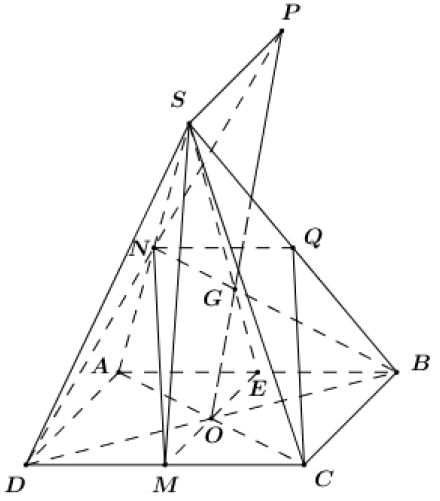
1) Tìm \[\left( {SAC} \right) \cap \left( {SBD} \right)\].
+ \[S\] là điểm chung thứ nhất.
+ Trong \[\left( {ABCD} \right)\] có \[AC \cap BD = 0\], ta có:
\[\left\{ \begin{array}{l}O \in AC \subset \left( {SAC} \right) \Rightarrow O \in \left( {SAC} \right)\\O \in BD \subset \left( {SBD} \right) \Rightarrow O \in \left( {SBD} \right)\end{array} \right. \Rightarrow O \in \left( {SAC} \right) \cap \left( {SBD} \right)\]
\[ \Rightarrow O\] là điểm chung thứ hai.
Vậy \[\left( {SAC} \right) \cap \left( {SBD} \right) = SO\].
2) Gọi \[Q\] là trung điểm của \[SB\].
\[NQ\] là đường trung bình của tam giác \[SAB \Rightarrow NQ//AB\] và \[NQ = \frac{1}{2}AB\].
\[ \Rightarrow NQ//MC\] và \[NQ = MC \Rightarrow MNQC\] là hình bình hành (dhnb).
\[ \Rightarrow MN//QC\]. Mà \[QC \subset \left( {SAB} \right)\].
Vậy \[MN//\left( {SAB} \right)\].
3) Gọi \[E\] là trung điểm của \[AB\] ta có \[\left( {SMG} \right) \equiv \left( {SME} \right)\].
Xác định \[\left( {SAD} \right) \cap \left( {SME} \right)\].
+ \[S\] là điểm chung thứ nhất.
+ \[\left\{ \begin{array}{l}AD \subset \left( {SAD} \right)\\ME \subset \left( {SME} \right)\\AD//ME\end{array} \right.\]
\[ \Rightarrow \] Giao tuyến của hai mặt phẳng \[\left( {SAD} \right)\] và \[\left( {SME} \right)\] là đường thẳng đi qua \[S\] và song song với
\[AD,\,\,ME\].
Qua \[S\] dựng đường thẳng song song với \[AD\] cắt \[OG\] tại \[P \Rightarrow \Delta \equiv SP\].
Nội \[BN\] ta có \[\left( {SAD} \right) \cap \left( {BDN} \right) = DN\].
\[\left\{ \begin{array}{l}P \in \Delta = \left( {SAD} \right) \cap \left( {SBC} \right) \Rightarrow P \in \left( {SAD} \right)\\P \in OQ \subset \left( {BDG} \right) \Rightarrow P \in \left( {BDG} \right)\end{array} \right. \Rightarrow P \in \left( {SAD} \right) \cap \left( {BDG} \right)\]
Vậy \[P \in DN\] hay \[P,N,D\] thẳng hàng.
Phương pháp:
1) Xác định hai điểm chung của hai mặt phẳng.
2) + Gọi \[Q\] là trung điểm của \[SB\].
+ Chứng minh \[MN\] song song với một đường thẳng bất kì chứa trong \[\left( {SBC} \right)\].
3) + Xác định \[\Delta \].
+ Xác định giao tuyến của \[\left( {SAD} \right)\] và \[\left( {BDG} \right)\].
+ Chứng minh \[P\] là điểm chung của hai mặt phẳng \[\left( {SAD} \right)\] và \[\left( {BDG} \right)\].
Cách giải:

1) Tìm \[\left( {SAC} \right) \cap \left( {SBD} \right)\].
+ \[S\] là điểm chung thứ nhất.
+ Trong \[\left( {ABCD} \right)\] có \[AC \cap BD = 0\], ta có:
\[\left\{ \begin{array}{l}O \in AC \subset \left( {SAC} \right) \Rightarrow O \in \left( {SAC} \right)\\O \in BD \subset \left( {SBD} \right) \Rightarrow O \in \left( {SBD} \right)\end{array} \right. \Rightarrow O \in \left( {SAC} \right) \cap \left( {SBD} \right)\]
\[ \Rightarrow O\] là điểm chung thứ hai.
Vậy \[\left( {SAC} \right) \cap \left( {SBD} \right) = SO\].
2) Gọi \[Q\] là trung điểm của \[SB\].
\[NQ\] là đường trung bình của tam giác \[SAB \Rightarrow NQ//AB\] và \[NQ = \frac{1}{2}AB\].
\[ \Rightarrow NQ//MC\] và \[NQ = MC \Rightarrow MNQC\] là hình bình hành (dhnb).
\[ \Rightarrow MN//QC\]. Mà \[QC \subset \left( {SAB} \right)\].
Vậy \[MN//\left( {SAB} \right)\].
3) Gọi \[E\] là trung điểm của \[AB\] ta có \[\left( {SMG} \right) \equiv \left( {SME} \right)\].
Xác định \[\left( {SAD} \right) \cap \left( {SME} \right)\].
+ \[S\] là điểm chung thứ nhất.
+ \[\left\{ \begin{array}{l}AD \subset \left( {SAD} \right)\\ME \subset \left( {SME} \right)\\AD//ME\end{array} \right.\]
\[ \Rightarrow \] Giao tuyến của hai mặt phẳng \[\left( {SAD} \right)\] và \[\left( {SME} \right)\] là đường thẳng đi qua \[S\] và song song với
\[AD,\,\,ME\].
Qua \[S\] dựng đường thẳng song song với \[AD\] cắt \[OG\] tại \[P \Rightarrow \Delta \equiv SP\].
Nội \[BN\] ta có \[\left( {SAD} \right) \cap \left( {BDN} \right) = DN\].
\[\left\{ \begin{array}{l}P \in \Delta = \left( {SAD} \right) \cap \left( {SBC} \right) \Rightarrow P \in \left( {SAD} \right)\\P \in OQ \subset \left( {BDG} \right) \Rightarrow P \in \left( {BDG} \right)\end{array} \right. \Rightarrow P \in \left( {SAD} \right) \cap \left( {BDG} \right)\]
Vậy \[P \in DN\] hay \[P,N,D\] thẳng hàng.
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
2) Một hộp có 6 bi đỏ, 7 bi xanh, 8 bi vàng (các bi khác nhau). Lấy ngẫu nhiên 6 bi. Tính xác suất để lấy được ít nhất 3 bi đỏ.
2) Một hộp có 6 bi đỏ, 7 bi xanh, 8 bi vàng (các bi khác nhau). Lấy ngẫu nhiên 6 bi. Tính xác suất để lấy được ít nhất 3 bi đỏ.
Câu 2:
Cho hình đa giác đều \[\left( H \right)\] có 36 đỉnh, chọn ngẫu nhiên 4 đỉnh của hình \[\left( H \right)\]. Tính xác suất để 4 đỉnh được chọn tạo thành hình vuông?
Câu 3:
Xác định số hạng không chứa \[x\] trong khai triển \[{\left( {{x^2} - \frac{2}{x}} \right)^6}\left( {x \ne 0} \right)\]
Câu 4:
1) Cho tập hợp \[A = \left\{ {0;1;2;3;4;5;6;7;8;9} \right\}\]. Có bao nhiêu số tự nhiên có 4 chữ số được thành lập từ tập hợp A.
1) Cho tập hợp \[A = \left\{ {0;1;2;3;4;5;6;7;8;9} \right\}\]. Có bao nhiêu số tự nhiên có 4 chữ số được thành lập từ tập hợp A.
Câu 5:
Từ một hộp chứa 12 quả cầu màu đỏ và 5 quả cầu màu xanh, lấy ngẫu nhiên đồng thời 3 quả cầu. Xác suất để lấy được 3 quả cầu màu xanh bằng:
Câu 6:
Cấp số cộng \[\left( {{u_n}} \right)\] có số hạng đầu \[{u_1}\] và công sai \[d\]. Công thức số hạng tổng quát của \[\left( {{u_n}} \right)\] là:
Câu 7:
Xác định số hạng không chứa \[x\] trong khai triển \[{\left( {{x^2} - \frac{2}{x}} \right)^6}\left( {x \ne 0} \right)\]
Câu 8:
Sắp xếp 6 chữ cái H, S, V, H, S, N thành một hàng. Tính xác suất sao cho 2 chữ cái giống nhau đứng cạnh nhau?
Câu 9:
Từ các chữ số 1, 2, 3, 4, 5, 6 có thể lập được bao nhiêu số tự nhiên chẵn có bốn chữ số đôi một khác nhau?
Câu 10:
1) Giải các phương trình sau:
a) \[2\sin x + \sqrt 2 = 0\];
b) \[\sqrt 3 \sin x - \cos x + 2 = 0\];
1) Giải các phương trình sau:
a) \[2\sin x + \sqrt 2 = 0\];
b) \[\sqrt 3 \sin x - \cos x + 2 = 0\];


