Cho hình đa giác đều \[\left( H \right)\] có 36 đỉnh, chọn ngẫu nhiên 4 đỉnh của hình \[\left( H \right)\]. Tính xác suất để 4 đỉnh được chọn tạo thành hình vuông?

Phương pháp:

+ Tính số phần tử của không gian mẫu.

+ Tính số phần tử của biến cố.

+ Tính xác suất của biến cố.

Cách giải:

Chọn ngẫu nhiên 4 đỉnh của hình \[\left( H \right) \Rightarrow n\left( \Omega \right) = C_{36}^4 = 58905\].

Giả sử \[{A_1},{A_2},{A_3},...,{A_{36}}\] là 36 đỉnh của đa giác đều \[\left( H \right)\]. Gọi \[O\] là tâm của đa giác đều \[\left( H \right)\].

\[ \Rightarrow {A_1}{A_2}...{A_{36}}\] là đa giác đều ngoại tiếp đường tròn \[\left( O \right)\].

Khi đó ta có \[{A_i}O{A_{i + 1}} = \frac{{360^\circ }}{{36}} = 10^\circ \,\,\forall i = \overline {1;36} \].

Để \[{A_x}{A_y}{A_z}{A_t}\] là hình vuông thì \[{A_x}O{A_y} = {A_y}O{A_z} = {A_z}O{A_t} = {A_t}O{A_x} = 90^\circ \].

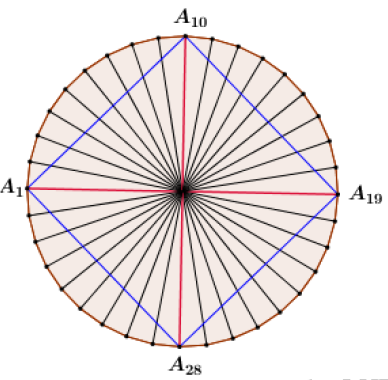
Ta có \[{O_1}O{A_{10}} = {A_{10}}O{A_{19}} = {A_{19}}O{A_{28}} = {A_{28}}O{A_1} = 90^\circ \Rightarrow {A_1}{A_{10}}{A_{19}}{A_{28}}\] là 1 hình vuông.

Cứ như vậy ta có các hình vuông là \[{A_2}{A_{11}}{A_{20}}{A_{29}},\,\,{A_3}{A_{12}}{A_{21}}{A_{30}},...,{A_9}{A_{18}}{A_{27}}{A_{36}}\].

Gọi A là biến cố: “4 đỉnh được chọn tạo thành hình vuông” \[ \Rightarrow n\left( A \right) = 9\].

Vậy \[P\left( A \right) = \frac{9}{{58905}} = \frac{1}{{6564}}\].