Giải Toán 10 Bài 2: Tổng và hiệu của hai vectơ
Sau bài học này chúng ta sẽ giải quyết được câu hỏi trên như sau:
Lời giải:
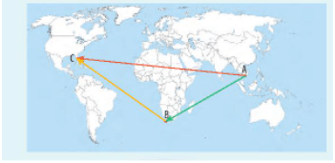
Vectơ biểu diễn tổng của hai độ dịch chuyển →AB+→BC là →AC.
1. Tổng của hai vectơ
Lời giải:
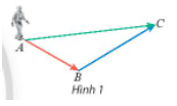
Vectơ biểu diễn độ dịch chuyển của rô bốt sau hai chuyển động trên là →AB+→BC.
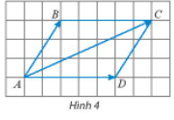
Hoạt động khám phá 2 trang 89 Toán lớp 10 Tập 1: Cho hình bình hành ABCD (Hình 4).
Chứng minh rằng →AB+→AD=→AC.
Lời giải:
Do ABCD là hình bình hành nên AD = BC và AD // BC.
Ta thấy hai vectơ →AD và →BC cùng hướng và |→AD|=|→BC| nên →AD=→BC.
Khi đó →AB+→AD=→AB+→BC=→AC.
Vậy →AB+→AD=→AC.
Lời giải:
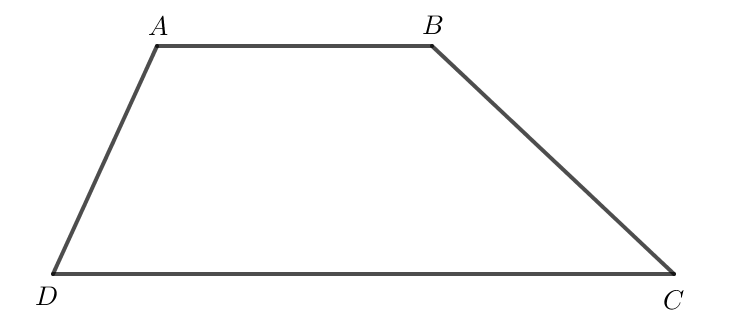
Ta có →a=→AC+→CB=→AB; →b=→DB+→BC=→DC.
Hình thang ABCD có hai đáy là AB và CD nên AB // CD.
Ta thấy hai vectơ →AB và →DC cùng hướng nên hai vectơ →a và →b cùng hướng.
Lời giải:
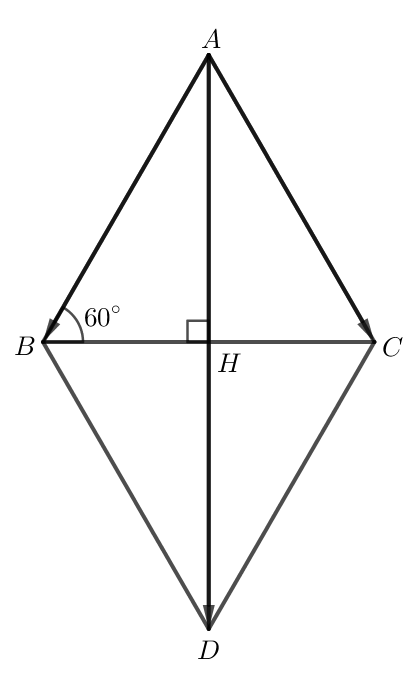
Dựng hình bình hành ABDC.
Do tam giác ABC đều nên ^ABC = 60o.
Hình bình hành ABDC có AB = AC nên ABDC là hình thoi.
Gọi giao điểm của AD và BC là H.
Khi đó AH ⊥ BC.
Tam giác ABH vuông tại H có:
sin^ABH=AHAB
⇒ AH = AB . sin ^ABH = a . sin 60o = a√32
Do H là giao điểm hai đường chéo của hình thoi ABDC nên AH = 12AD.
Do đó AD = a√3.
Áp dụng quy tắc hình bình hành ta có →AB+→AC=→AD.
Do đó |→AB+→AC|=|→AD|=a√3.
Lời giải:
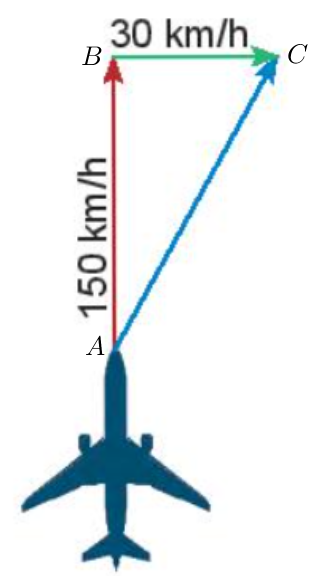
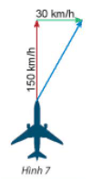
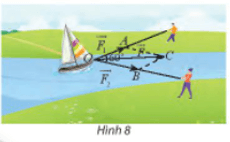
Gọi vectơ →AB là vectơ vận tốc của máy bay, vectơ →BC là vận tốc gió.
Khi đó vectơ tổng của hai vectơ nói trên là →AB+→BC=→AC.
Khi đó tam giác ABC vuông tại B.
Áp dụng định lý Pythagore vào tam giác ABC vuông tại B:
AC2 = AB2 + BC2
⇒ AC2 = 1502 + 302
⇒ AC2 = 23 400
⇒ AC = 30√26 km/h (do AC là độ dài đoạn thẳng nên AC > 0).
Vậy |→AB+→BC|=|→AC|=30√26.
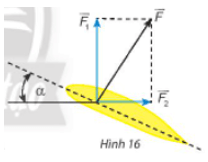
Lời giải:
Dựng hình bình hành AOBC.
Khi đó →F=→OC.
Do AOBC là hình bình hành nên ^AOB+^OBC=180° và OA = BC = 400.
Do đó .
Áp dụng định lí côsin vào tam giác OBC có:
OC2 = OB2 + BC2 - 2.OB.BC.cos
OC2 = 6002 + 4002 - 2.600.400.cos 120o
OC2 = 760 000
OC ≈ 872 N (do OC là độ dài đoạn thẳng nên OC > 0)
Vậy ≈ 872 N.
2. Tính chất của phép cộng các vectơ
Hoạt động khám phá 2 trang 90 Toán lớp 10 Tập 1: Cho ba vectơ được biểu diễn như Hình 9.
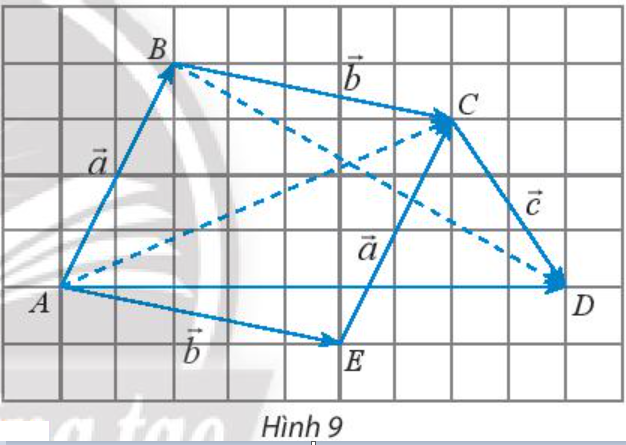
Hãy hoàn thành các phép cộng vectơ sau và so sánh các kết quả tìm được:
a) ;
b) ;
Lời giải:
a) Ta có: .
.
Do đó .
b) Ta có: .
.
Do đó .
a) ;
b) .
Lời giải:
a)
Do đó = 1.
b)
Do đó .
Áp dụng định lí Pythagore vào tam giác ADC có:
AC2 = AD2 + DC2
AC2 = 12 + 12
AC2 = 2
AC = (do AC là độ dài đoạn thẳng)
Vậy .
3. Hiệu của hai vectơ
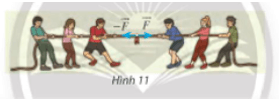
Hoạt động khám phá 3 trang 91 Toán lớp 10 Tập 1: Tìm hợp lực của hai lực đối nhau và (Hình 11).
Lời giải:
Hợp lực của hai lực đối nhau và là .
a) ;
b) .
Lời giải:
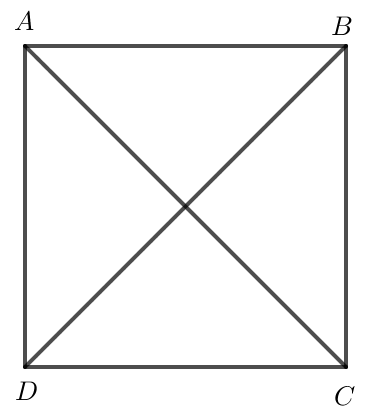
a) Ta có .
Do đó .
Áp dụng định lí Pythagore vào tam giác ABD vuông tại A có:
BD2 = AB2 + AD2
BD2 = 12 + 12
BD2 = 2
BD = (do BD là độ dài đoạn thẳng nên BD > 0)
Vậy .
b) Ta có .
Do đó = 1.
4. Tính chất vectơ của trung điểm đoạn thẳng và trọng tâm tam giác
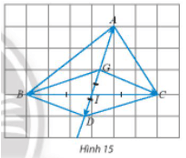
b) Cho điểm G là trọng tâm của tam giác ABC có trung tuyến AI. Lấy D là điểm đối xứng với G qua I. Ta có BGCD là hình bình hành và G là trung điểm của đoạn thẳng AD. Với lưu ý rằng và , hoàn thành phép cộng vectơ sau:
Lời giải:
a) Ta có
b) Ta có
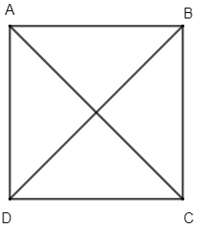
a) ;
b) ;
c) .
Lời giải:
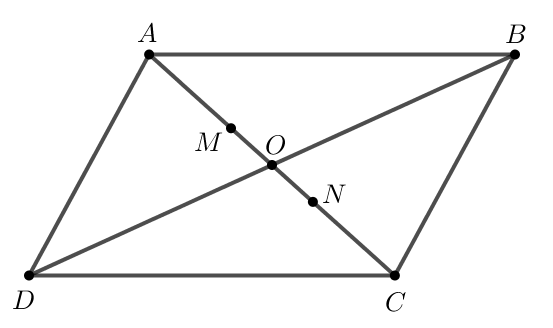
a) Hình bình hành ABCD có tâm O nên O là trung điểm của BD.
Do nên M là trọng tâm của tam giác ADB.
Khi đó trên AO chọn M sao cho .
b) Do nên N là trọng tâm của tam giác DBC.
Khi đó trên CO chọn N sao cho .
c) Do nên P là trung điểm của MN (1).
Ta có AM = AO = AC = AC; CN = CO = AC = AC.
Do đó MN = AC.
MO = AO = AC = AC.
Khi đó MO = MN.
Mà O nằm giữa M và N nên O là trung điểm của MN (2).
Từ (1) và (2) suy ra P trùng O.
Bài tập
a) ;
b)
Lời giải:
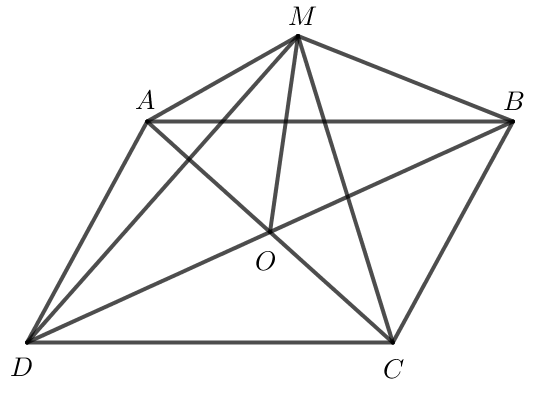
a) Do ABCD là hình bình hành nên AB // CD, AB = CD.
Ta thấy hai vectơ và ngược hướng và nên .
Do đó .
b) Do O là giao điểm hai đường chéo của hình bình hành ABCD nên O là trung điểm của AC và BD.
Do O là trung điểm của AC nên .
Do O là trung điểm của BD nên .
Ta có .
.
Do đó .
Bài 2 trang 93 Toán lớp 10 Tập 1: Cho tứ giác ABCD, thực hiện các phép cộng và trừ vectơ sau:
a) ;
b) ;
c) .
Lời giải:
a)
b) .
c) .
Bài 3 trang 93 Toán lớp 10 Tập 1: Cho tam giác đều ABC cạnh bằng a. Tính độ dài của các vectơ:
a) ;
b) ;
c) .
Lời giải:
a) Ta có .
Do đó = a.
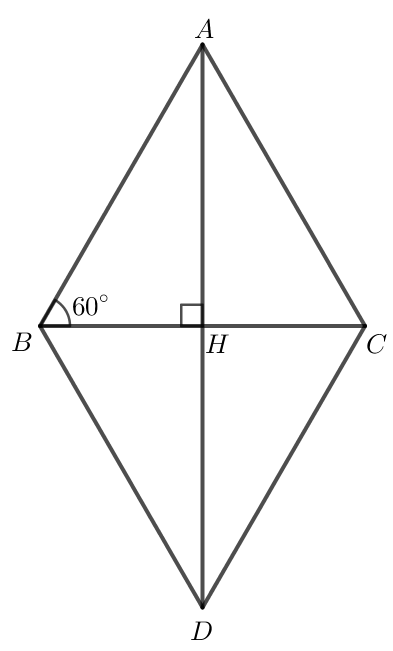
b) Dựng hình bình hành ABDC.
Gọi H là giao điểm của AD và BC.
Áp dụng quy tắc hình bình hành ta có .
Hình bình hành ABDC có AB = AC nên ABDC là hình thoi.
Do đó AD BC tại H.
Do tam giác ABC đều nên = 60o.
Xét tam giác ABH vuông tại H:
AH = AB . sin = a . sin 60o = .
Do H là giao điểm hai đường chéo của hình thoi ABDC nên H là trung điểm của AD.
Do đó AD = 2AH = 2 . = .
Vậy .
c) Ta có .
Do đó = a.
a) ;
b)
Lời giải:
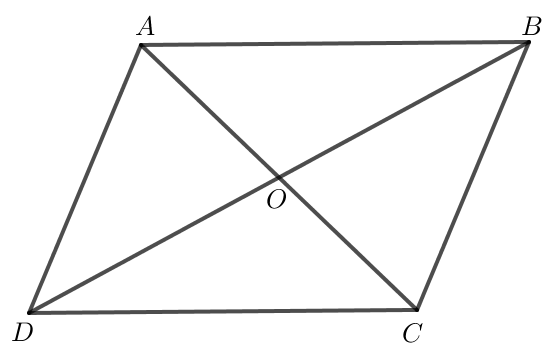
a) Ta có ; .
Do ABCD là hình bình hành nên AB = CD.
Ta thấy hai vectơ và cùng hướng và nên .
Do đó .
b) Ta có .
Do đó .
Vậy .
Lời giải:
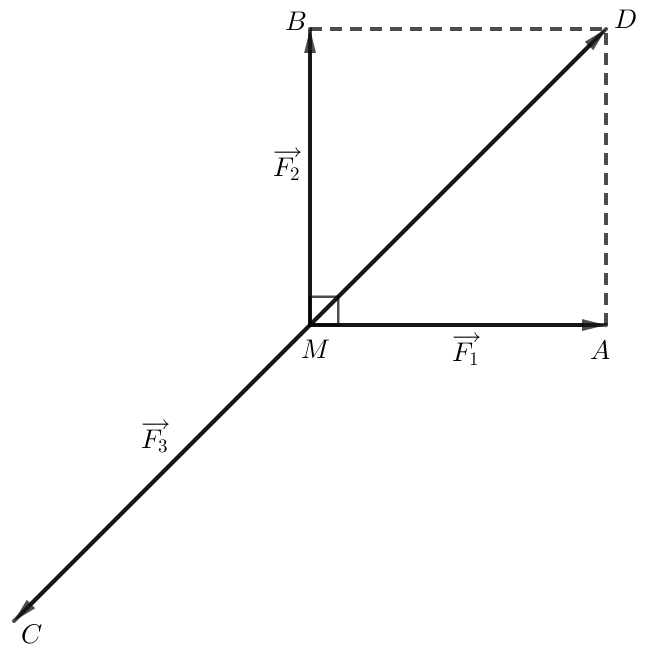
Dựng hình bình hành MBAD.
Do ba lực và cùng tác động vào vật tại điểm M và vật đứng yên nên
.
Do đó .
Áp dụng quy tắc hình bình hành ta có:
hay .
Do đó .
Hình bình hành MBAD có = 90o và MA = MB nên MBAD là hình vuông.
Áp dụng định lí Pythagore vào tam giác MAD vuông tại A có:
MD2 = MA2 + AD2
MD2 = 102 + 102
MD2 = 2.102
MD = N (do MD là độ dài đoạn thẳng nên MD > 0).
N.
Vậy cường độ của lực là N.
Lời giải:
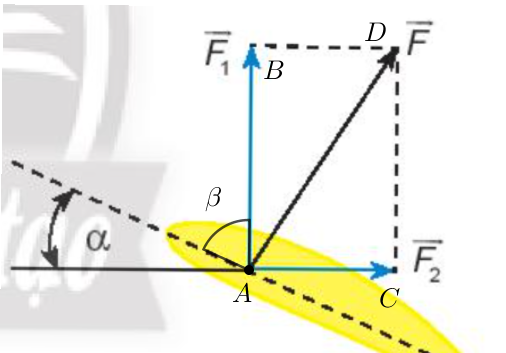
Đặt tên các điểm đầu và điểm cuối của các vectơ và tên góc như trên hình.
Khi đó ABDC là hình chữ nhật.
Ta có = α (cùng phụ với β).
Do đó = 30o.
Tam giác ABD vuông tại B nên
BA = AD . cos = a . cos 30o = .
BD = AD. sin = a . sin 30o = .
Do ABDC là hình chữ nhật nên BD = AC = .
Vậy .
Lời giải:
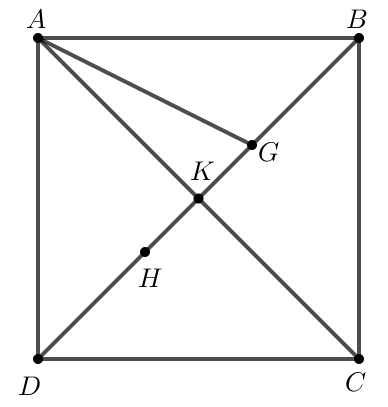
Do nên K là trung điểm của AC.
Do đó K là giao điểm hai đường chéo của hình vuông ABCD.
Do nên G là trọng tâm của tam giác ABC.
Khi đó trên đoạn BK chọn điểm G sao cho .
Do nên H là trọng tâm của tam giác ADC.
Khi đó trên đoạn DK chọn điểm H sao cho .
Áp dụng định lí Pythagore vào tam giác ADC vuông tại D có:
AC2 = AD2 + DC2
AC2 = a2 + a2
AC2 = 2a2
AC = a (do AC là độ dài đoạn thẳng nên AC > 0)
Do K là trung điểm của AC nên AK = AC = .
Do đó .
Do ABCD là hình vuông nên AC = BD.
Do đó BD = a.
Do H là trọng tâm của tam giác ADC nên HK = DK = BD = BD = .
Do G là trọng tâm của tam giác ABC nên KG = BK = BD = BD = .
Do đó HK + KG = + hay HG = .
Do đó .
Do ABCD là hình vuông là K là giao điểm hai đường chéo nên AC BD tại K.
Áp dụng định lí Pythagore vào tam giác AKG vuông tại K có:
AG2 = AK2 + KG2
AG2 =
AG2 =
AG = (do AG là độ dài đoạn thẳng nên AG > 0)
Do đó .
Vậy ; ; .
Lời giải:
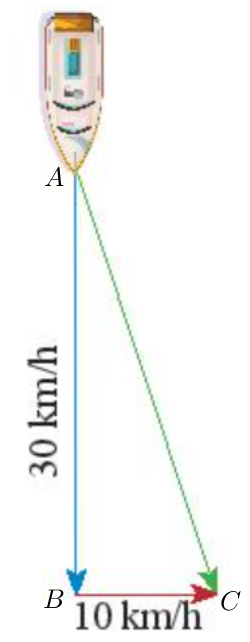
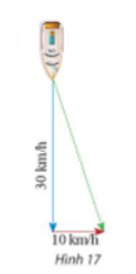
Đặt tên điểm đầu và điểm cuối của các vectơ như hình trên.
Khi đó vectơ vận tốc của con tàu là vectơ ; vectơ vận tốc của dòng nước là vectơ .
Khi đó vectơ tổng của hai vectơ trên là .
Áp dụng định lí Pythagore vào tam giác ABC vuông tại B:
AC2 = AB2 + BC2
AC2 = 302 + 102
AC2 = 1 000
AC = (do AC là độ dài đoạn thẳng nên AC > 0)
Vậy độ dài tổng của hai vectơ trên là km/h.
Xem thêm lời giải bài tập SGK Toán lớp 10 Chân trời sáng tạo hay, chi tiết khác:
Bài 3: Tích của một số với một vectơ