Cho hình vuông ABCD có cạnh bằng a và ba điểm G, H, K thỏa mãn: vectơ KA + vectơ KC = vectơ 0; vectơ GA + vectơ GB + vectơ GC = vectơ 0

Bài 7 trang 93 Toán lớp 10 Tập 1: Cho hình vuông ABCD có cạnh bằng a và ba điểm G, H, K thỏa mãn: $\overrightarrow{KA}+\overrightarrow{KC}=\overrightarrow{0};\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}=\overrightarrow{0}$; $\overrightarrow{HA}+\overrightarrow{HD}+\overrightarrow{HC}=\overrightarrow{0}$. Tính độ dài các vectơ $\overrightarrow{KA},\overrightarrow{GH},\overrightarrow{AG}$.

Trả lời

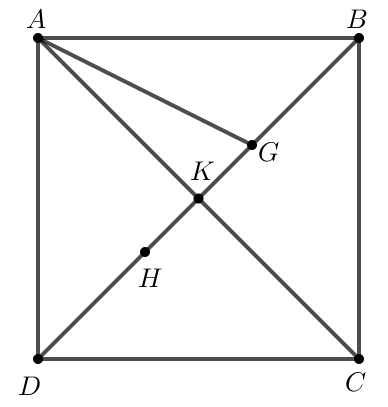
Do $\overrightarrow{K\text{A}}+\overrightarrow{KC}=\overrightarrow{0}$ nên K là trung điểm của AC.

Do đó K là giao điểm hai đường chéo của hình vuông ABCD.

Do $\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}=\overrightarrow{0}$ nên G là trọng tâm của tam giác ABC.

Khi đó trên đoạn BK chọn điểm G sao cho $\overrightarrow{BG}=\frac{2}{3}\overrightarrow{BK}$.

Do $\overrightarrow{HA}+\overrightarrow{H\text{D}}+\overrightarrow{HC}=\overrightarrow{0}$ nên H là trọng tâm của tam giác ADC.

Khi đó trên đoạn DK chọn điểm H sao cho $\overrightarrow{DH}=\frac{2}{3}\overrightarrow{DK}$.

Áp dụng định lí Pythagore vào tam giác ADC vuông tại D có:

AC² = AD² + DC²

$\Rightarrow$ AC² = a² + a²

$\Rightarrow$ AC² = 2a²

$\Rightarrow$ AC = $\sqrt{2}$a (do AC là độ dài đoạn thẳng nên AC > 0)

Do K là trung điểm của AC nên AK = $\frac{1}{2}$AC = $\frac{\sqrt{2}a}{2}$.

Do đó $\left|\overrightarrow{K\text{A}}\right|=\frac{\sqrt{2}a}{2}$.

Do ABCD là hình vuông nên AC = BD.

Do đó BD = $\sqrt{2}$a.

Do H là trọng tâm của tam giác ADC nên HK = $\frac{1}{3}$DK = $\frac{1}{3}.\frac{1}{2}$BD = $\frac{1}{6}$BD = $\frac{\sqrt{2}a}{6}$.

Do G là trọng tâm của tam giác ABC nên KG = $\frac{1}{3}$BK = $\frac{1}{3}.\frac{1}{2}$BD = $\frac{1}{6}$BD = $\frac{\sqrt{2}a}{6}$.

Do đó HK + KG = $\frac{\sqrt{2}a}{6}$+ $\frac{\sqrt{2}a}{6}$ hay HG = $\frac{\sqrt{2}a}{3}$.

Do đó $\left|\overrightarrow{GH}\right|=\frac{\sqrt{2}a}{3}$.

Do ABCD là hình vuông là K là giao điểm hai đường chéo nên AC $\perp$ BD tại K.

Áp dụng định lí Pythagore vào tam giác AKG vuông tại K có:

AG² = AK² + KG²

$\Rightarrow$ AG² = ${\left(\frac{\sqrt{2}a}{2}\right)}^2+{\left(\frac{\sqrt{2}a}{6}\right)}^2$

$\Rightarrow$ AG² = $\frac{5{\text{a}}^2}{9}$

$\Rightarrow$ AG = $\frac{\sqrt{5}a}{3}$ (do AG là độ dài đoạn thẳng nên AG > 0)

Do đó $\left|\overrightarrow{AG}\right|=\frac{\sqrt{5}a}{3}$.

Vậy $\left|\overrightarrow{K\text{A}}\right|=\frac{\sqrt{2}a}{2}$; $\left|\overrightarrow{GH}\right|=\frac{\sqrt{2}a}{3}$; $\left|\overrightarrow{AG}\right|=\frac{\sqrt{5}a}{3}$.

Xem thêm lời giải bài tập SGK Toán lớp 10 Chân trời sáng tạo hay, chi tiết khác:

Bài tập cuối chương 4

Bài 1: Khái niệm vectơ

Bài 2: Tổng và hiệu của hai vectơ

Bài 3: Tích của một số với một vectơ

Bài 4: Tích vô hướng của hai vectơ

Bài tập cuối chương 5