Cho tam giác đều ABC cạnh bằng a. Tính độ dài của các vectơ: a) vectơ BA + vectơ AC

Bài 3 trang 93 Toán lớp 10 Tập 1: Cho tam giác đều ABC cạnh bằng a. Tính độ dài của các vectơ:

a) $\overrightarrow{BA}+\overrightarrow{AC}$;

b) $\overrightarrow{AB}+\overrightarrow{AC}$;

c) $\overrightarrow{BA}-\overrightarrow{BC}$.

Trả lời

a) Ta có $\overrightarrow{BA}+\overrightarrow{AC}=\overrightarrow{BC}$.

Do đó $\left|\overrightarrow{BA}+\overrightarrow{AC}\right|=\left|\overrightarrow{BC}\right|$ = a.

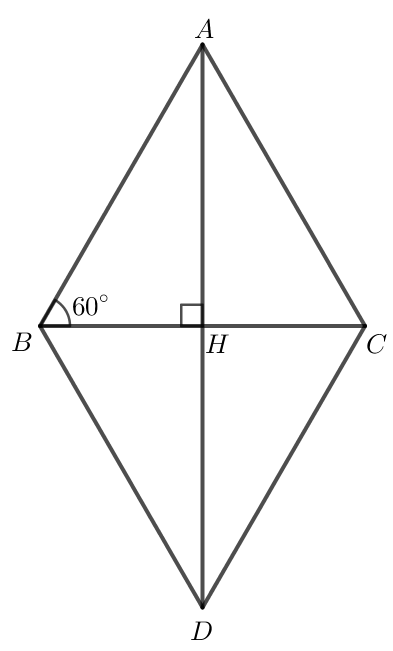
b) Dựng hình bình hành ABDC.

Gọi H là giao điểm của AD và BC.

Áp dụng quy tắc hình bình hành ta có $\overrightarrow{AB}+\overrightarrow{AC}=\overrightarrow{A\text{D}}$.

Hình bình hành ABDC có AB = AC nên ABDC là hình thoi.

Do đó AD $\perp$ BC tại H.

Do tam giác ABC đều nên $\widehat{ABH}$ = 60^o.

Xét tam giác ABH vuông tại H:

$\sin \widehat{ABH}=\frac{AH}{AB}$

$\Rightarrow$ AH = AB . sin $\widehat{ABH}$ = a . sin 60^o = $\frac{a\sqrt{3}}{2}$.

Do H là giao điểm hai đường chéo của hình thoi ABDC nên H là trung điểm của AD.

Do đó AD = 2AH = 2 . $\frac{a\sqrt{3}}{2}$ = $a\sqrt{3}$.

Vậy $\left|\overrightarrow{AB}+\overrightarrow{AC}\right|=\left|\overrightarrow{A\text{D}}\right|=a\sqrt{3}$.

c) Ta có $\overrightarrow{BA}-\overrightarrow{BC}=\overrightarrow{CA}$.

Do đó $\left|\overrightarrow{BA}-\overrightarrow{BC}\right|=\left|\overrightarrow{CA}\right|$= a.

Xem thêm lời giải bài tập SGK Toán lớp 10 Chân trời sáng tạo hay, chi tiết khác:

Bài tập cuối chương 4

Bài 1: Khái niệm vectơ

Bài 2: Tổng và hiệu của hai vectơ

Bài 3: Tích của một số với một vectơ

Bài 4: Tích vô hướng của hai vectơ

Bài tập cuối chương 5