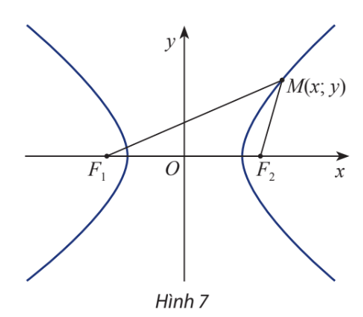
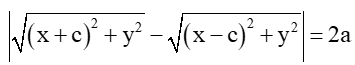Cho hypebol (H) có các tiêu điểm F1 và F2 và đặt F1F2 = 2c. Điểm M thuộc hypecbol (H) khi và chỉ khi |F1M – F2M| = 2a

Hoạt động khám phá 4 trang 66 Toán lớp 10 Tập 2: Cho hypebol (H) có các tiêu điểm F₁ và F₂ và đặt F₁F₂ = 2c. Điểm M thuộc hypecbol (H) khi và chỉ khi |F₁M – F₂M| = 2a. Chọn hệ trục tọa độ Oxy sao cho F₁(-c; 0) và F₂(c; 0). Xét điểm M(x; y).

a) Tính F₁M và F₂M theo x, y và c.

b) Giải thích các phát biểu sau:

M(x; y) ∈ (H) ⇔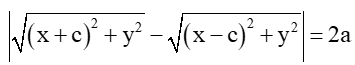 

Trả lời

a) Ta có: $\overrightarrow{F_{1}M}\left(x+c;y\right)$ ⇒ $F_{1}M=\sqrt{{\left(x+c\right)}^2+y^2}$

$\overrightarrow{F_{2}M}\left(x-c;y\right)$ ⇒ $F_{2}M=\sqrt{{\left(x-c\right)}^2+y^2}$

Vậy $F_{1}M=\sqrt{{\left(x+c\right)}^2+y^2}$ và $F_{2}M=\sqrt{{\left(x-c\right)}^2+y^2}$.

b) +) Ta có: Elip (E) là tập hợp các điểm M trong mặt phẳng sao cho F₁M + F₂M = 2a.

Nếu M thuộc elip (E) thì F₁M + F₂M = 2a hay $\sqrt{{\left(x+c\right)}^2+y^2}+\sqrt{{\left(x-c\right)}^2+y^2}=2a$.

+) Nếu điểm M(x; y) có tọa độ thỏa mãn $\sqrt{{\left(x+c\right)}^2+y^2}+\sqrt{{\left(x-c\right)}^2+y^2}=2a$ hay F₁M + F₂M = 2a thì M là điểm thỏa mãn F₁M + F₂M = 2a.

Xem thêm lời giải bài tập SGK Toán lớp 10 Chân trời sáng tạo hay, chi tiết khác:

Bài 2: Đường thẳng trong mặt phẳng toạ độ

Bài 3: Đường tròn trong mặt phẳng toạ độ

Bài 4: Ba đường conic trong mặt phẳng tọa độ

Bài tập cuối chương 9

Bài 1: Không gian mẫu và biến cố

Bài 2: Xác suất của biến cố