Một cổng chào có hình parabol cao 10m và bề rộng của cổng tại chân cổng là 5m. Tính bề rộng của cổng tại chỗ cách đỉnh 2m
1.2k
13/06/2023
Vận dụng 3 trang 70 Toán lớp 10 Tập 2: Một cổng chào có hình parabol cao 10m và bề rộng của cổng tại chân cổng là 5m. Tính bề rộng của cổng tại chỗ cách đỉnh 2m.
Trả lời
Ta vẽ parabol biểu diễn cho cổng chào như sau:
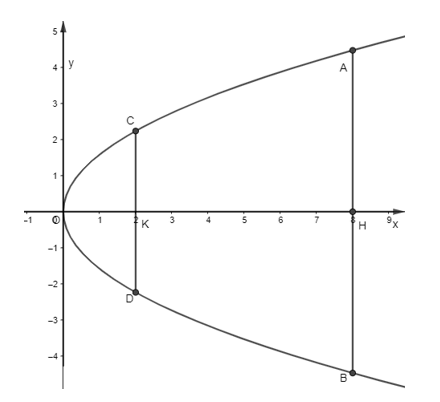
Gọi phương trình của parabol là y2 = 2px.
Ta có chiều cao của cổng là OH = 10, bề rộng của cổng là AB = 5.
Khi đó A(10; 2,5), thay tọa độ điểm A vào parabol y2 = 2px, ta được:
2,52 = 2p.10
⇔ 254 = 20p
⇔ p = 254.20=516
Suy ra parabol có phương tình y2 = 2.516.x ⇔ y2 = 58.x
Tại vị trí điểm K cách đỉnh 2m bề rộng của cổng là đoạn CD.
Gọi C(2; yC) (yC > 0)
Vì C thuộc parabol nên tọa độ của C thỏa mãn y2 = 58.x nên ta có:
y2C = 58.2
⇔ y2C = 54
⇔ yC = √52
⇒ C = (0; √52).
Khi đó CD = 2|yC|= 2.√52 = √5 .
Vậy bề rộng của cộng tại chỗ cách đỉnh 2m là √5m.
Xem thêm lời giải bài tập SGK Toán lớp 10 Chân trời sáng tạo hay, chi tiết khác:
Bài 2: Đường thẳng trong mặt phẳng toạ độ
Bài 3: Đường tròn trong mặt phẳng toạ độ
Bài 4: Ba đường conic trong mặt phẳng tọa độ
Bài tập cuối chương 9
Bài 1: Không gian mẫu và biến cố
Bài 2: Xác suất của biến cố

