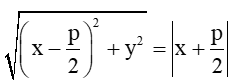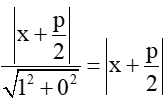Cho parabol (P) có tiêu điểm F và đường chuẩn ∆. Gọi khoảng cách từ tiêu điểm đến đường chuẩn là p, hiển nhiên p > 0
463
13/06/2023
Hoạt động khám phá 6 trang 68 Toán lớp 10 Tập 2: Cho parabol (P) có tiêu điểm F và đường chuẩn ∆. Gọi khoảng cách từ tiêu điểm đến đường chuẩn là p, hiển nhiên p > 0.
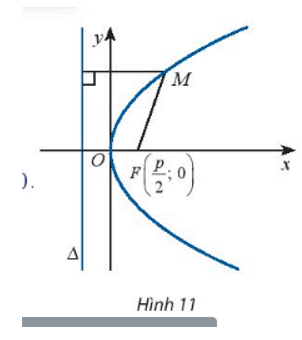
Chọn hệ trục tọa độ Oxy sao cho F(p2;0) và ∆: x + p2 = 0. Xét điểm M(x; y).
a) Tính MF và d(M. ∆).
b) Giải thích phát biểu sau:
M(x; y) ∈ (P) ⇔ 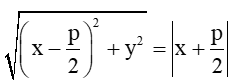 .
.
Trả lời
a) Ta có: →FM=(x−p2;y) ⇒ MF = √(x−p2)2+y2
Khoảng cách từ điểm M đến đường thẳng ∆ là:
d(M, ∆) = 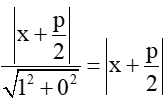
b) +) Ta có M(x; y) ∈ (P) cần chứng minh 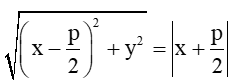 .
.
Vì M(x; y) ∈ (P) nên M cách đều F và ∆
⇒ MF = d(M, ∆) hay 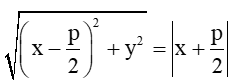 (1).
(1).
+) Ta có điểm M(x; y) thỏa mãn 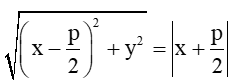 thì M(x; y) ∈ (P).
thì M(x; y) ∈ (P).
Ta có 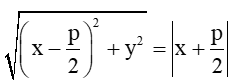
⇒ MF = d(M, ∆)
Nghĩa là điểm M thỏa mãn cách đều tiêu điểm F và đường chuẩn ∆. Do đó điểm M thuộc parabol (P) (2)
Từ (1) và (2) suy ra điều phải chứng minh.
Xem thêm lời giải bài tập SGK Toán lớp 10 Chân trời sáng tạo hay, chi tiết khác:
Bài 2: Đường thẳng trong mặt phẳng toạ độ
Bài 3: Đường tròn trong mặt phẳng toạ độ
Bài 4: Ba đường conic trong mặt phẳng tọa độ
Bài tập cuối chương 9
Bài 1: Không gian mẫu và biến cố
Bài 2: Xác suất của biến cố