50 câu hỏi trắc nghiệm thuộc Đề kiểm tra Giữa kì 2 Toán 11 có đáp án (Mới nhất) (Đề 23)

Đề kiểm tra Giữa kì 2 Toán 11 có đáp án (Mới nhất)

Đề kiểm tra Giữa kì 2 Toán 11 có đáp án (Mới nhất) (Đề 23)

1271 lượt thi
50 câu hỏi
0 phút

BẮT ĐẦU LÀM BÀI

Danh sách câu hỏi

Câu 1:

Cho tam giác đều ABC có cạnh bằng 2a. Người ta dựng tam giác đều $A_{1} B_{1} C_{1}$ có cạnh bằng đường cao của tam giác ABC; dựng tam giác đều $A_{2} B_{2} C_{2}$ có cạnh bằng đường cao của tam giác $A_{1} B_{1} C_{1}$ và cứ tiếp tục như vậy. Giả sử cách dựng trên có thể tiến ra vô hạn. Nếu tổng diện tích S của tất cả các tam giác đều ABC, $A_{1} B_{1} C_{1}$ , $A_{2} B_{2} C_{2}$ ,… bằng $24 \sqrt{3}$ thì a bằng:

A. $4 \sqrt{3}$

B. 3

C. $\sqrt{6}$

D. $3 \sqrt{3}$

Lời giải

Chọn C

Ta có độ dài đường cao của tam giác đều ABC có cạnh bằng 2a là $2 a \frac{\sqrt{3}}{2} = a \sqrt{3}$ nên tam giác $A_{1} B_{1} C_{1}$ có cạnh bằng $a \sqrt{3}$ . Do đó hai tam giác ABC và $A_{1} B_{1} C_{1}$ dồng dạng với nhau với tỉ số đồng dạng là .

Suy ra $\frac{S_{A_{1} B_{1} C_{1}}}{S_{A B C}} = k^{2} = \frac{3}{4} \Rightarrow S_{A_{1} B_{1} C_{1}} = \frac{3}{4} S_{A B C}$ .

Tương tự ta có $S_{A_{2} B_{2} C_{2}} = \frac{3}{4} S_{A_{1} B_{1} C_{1}}$ , $S_{A_{3} B_{3} C_{3}} = \frac{3}{4} S_{A_{2} B_{2} C_{2}}$ ,…

Nên dãy số 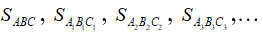là một cấp số nhân lùi vô hạn với công bội $q = \frac{3}{4}$ và số hạng đầu $S_{A B C} = {(2 a)}^{2} \frac{\sqrt{3}}{4} = a^{2} \sqrt{3}$ .

Suy ra tổng diện tích của tất cả các tam giác đều ABC, $A_{1} B_{1} C_{1}$ , $A_{2} B_{2} C_{2}$ ,… bằng

$S = \frac{S_{A B C}}{1 - q} = \frac{a^{2} \sqrt{3}}{1 - \frac{3}{4}} = 4 a^{2} \sqrt{3}$ .

Ta có $4 a^{2} \sqrt{3} = 24 \sqrt{3} \Leftrightarrow a = \sqrt{6}$ .

Câu 2:

Trong các giới hạn sau, giới hạn nào bằng 0?

A. $\lim \frac{1 - n}{2 n + 1}$

B. $\lim {(\frac{3}{2})}^{n}$

C. $\lim {(\frac{π}{4})}^{n}$

D. $\lim n^{2}$

Lời giải

Chọn C

Ta có $|\frac{π}{4}| < 1 \Rightarrow \lim {(\frac{π}{4})}^{n} = 0$ .

Câu 3:

\lim \frac{{(1 - 2 n)}^{3}}{a n^{3} + 2} = 4

với a là tham số. Khi đó

a - a^{2}

A. -4

B. -6

C. -2

D. 0

Lời giải

Chọn B

Ta có $\lim \frac{{(1 - 2 n)}^{3}}{a n^{3} + 2} = \lim \frac{{(\frac{1}{n} - 2)}^{3}}{a + \frac{2}{n^{3}}} = \frac{- 8}{a}$ . Theo giả thiết ta có $\frac{- 8}{a} = 4 \Rightarrow a = - 2$ .

Suy ra $a - a^{2} = - 6$ .

Câu 4:

Cho hình tứ diện ABCD . Gọi M,N lần lượt là trung điểm của AB và CD , I là trung điểm của đoạn MN . Mệnh đề nào sau đây sai?

A. $\vec{M N} = \frac{1}{2} (\vec{A D} + \vec{C B})$

B. $\vec{A N} = \frac{1}{2} (\vec{A C} + \vec{A D})$

C. $\vec{M A} + \vec{M B} = \vec{0}$

D. $\vec{I A} + \vec{I B} + \vec{I C} + \vec{I D} = \vec{0}$

Lời giải

Chọn A

Cho hình tứ diện ABCD . Gọi M,N lần lượt là trung điểm của AB và CD , I là trung điểm của đoạn MN . Mệnh đề nào sau đây sai? (ảnh 1)

Ta có $\vec{M N} = \frac{1}{2} (\vec{M C} + \vec{M D}) = \frac{1}{2} (\vec{M B} + \vec{B C} + \vec{M A} + \vec{A D}) = = \frac{1}{2} (\vec{B C} + \vec{A D}) = \frac{1}{2} (\vec{A D} - \vec{C B})$

Câu 5:

Trong các mệnh đề sau, mệnh đề nào sai?

A. $\lim_{x \to - \infty} (\sqrt{x^{2} - x + 1} - x) = - \frac{1}{2}$

B. $\lim_{x \to - \infty} (\frac{\sqrt{x^{2} - x + 1} - 2}{2 x + 3}) = \frac{1}{2}$

C. $\lim_{x \to - 1^{-}} \frac{3 x + 2}{x + 1} = + \infty$

D. $\lim_{x \to + \infty} \frac{3 x - 2}{2 - x} = - 3$

Lời giải

Chọn A

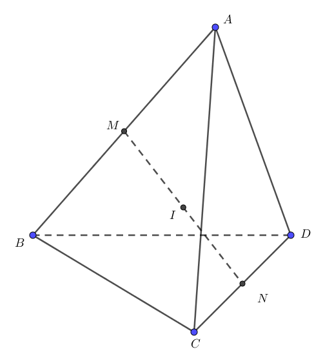
Ta có $\lim_{x \to - \infty} (\sqrt{x^{2} - x + 1} - x) = \lim_{x \to - \infty} x (- \sqrt{1 - \frac{1}{x} + \frac{1}{x^{2}}} - 1)$

Vì $\lim_{x \to - \infty} x = - \infty$ và $\lim_{x \to - \infty} (- \sqrt{1 - \frac{1}{x} + \frac{1}{x^{2}}} - 1) = - 2 < 0$ nên $\lim_{x \to - \infty} (\sqrt{x^{2} - x + 1} - x) = + \infty$ .

Câu 6:

Cho hình lập phương ABCCDA'B'C'D' . Khẳng định nào sau đây sai?

A. Góc giữa 2 đường thẳng B'D' và AA' bằng $60 °$ .

B. Góc giữa 2 đường thẳng AC và B'D' bằng

90 °

.

C. Góc giữa 2 đường thẳng AB và D'C' bằng 45

°

D. Góc giữa 2 đường thẳng D'C và A'C' bằng 60

°

.

Lời giải

Chọn A

Media VietJack

A sai vì $A A^{'} ⊥ (A^{'} B^{'} C^{'} D^{'}) \Rightarrow A A^{'} ⊥ B^{'} D^{'}$

Câu 7:

Tính giới hạn $\lim \frac{2017^{n} - 2019^{n - 2}}{{3.2018}^{n} - 2019^{n - 1}}$ là

A. $\frac{- 1}{2019}$

B. $\frac{1}{2019}$

C. -2019

D. 0

Chọn B

$\lim \frac{2017^{n} - 2019^{n - 2}}{{3.2018}^{n} - 2019^{n - 1}} = \lim \frac{2017^{2} . {(\frac{2017}{2019})}^{n - 2} - 1}{{3.2018}^{2} . {(\frac{2018}{2019})}^{n - 2} - 2019} = \frac{1}{2019}$

Câu 8:

Tính giới hạn $J = \lim \frac{(n - 1) (2 n + 3)}{n^{3} + 2}$ là

A. J=3

B. J=1

C. J=0

D. J=2

Lời giải

Chọn C

$J = \lim \frac{(n - 1) (2 n + 3)}{n^{3} + 2} = \lim \frac{\frac{1}{n} (1 - \frac{1}{n}) (2 + \frac{3}{n})}{1 + \frac{2}{n^{3}}} = 0$ .

Câu 9:

Có bao nhiêu giá trị m nguyên thuộc đoạn [-20,20] để $\lim_{x \to - \infty} (m x - 2) (m - 3 x^{2}) = - \infty$ ?

A. 21

B. 22

C. 20

D. 41

Lời giải

Chọn C

+) Nếu m=0 thì $\lim_{x \to - \infty} (m x - 2) (m - 3 x^{2}) = \lim_{x \to - \infty} (- 2) (- 3 x^{2}) \lim_{x \to - \infty} 6 x^{2} = + \infty$

$\Rightarrow m = 0$ không thỏa mãn.

+) Nếu m=0 thì

$\lim_{x \to - \infty} (m x - 2) (m - 3 x^{2}) = \lim_{x \to - \infty} (- 3 m x^{3} + 6 x^{2} + m^{2} x - 2 m) = \lim_{x \to - \infty} [x^{3} (- 3 m + 6. \frac{1}{x} + m^{2} \frac{1}{x^{2}} - 2 m \frac{1}{x^{3}})]$ Vậy để $\lim_{x \to - \infty} (m x - 2) (m - 3 x^{2}) = - \infty$ thì m<0, do đó có 20 số nguyên thỏa mãn.

Câu 10:

Hàm số nào sau đây không liên tục tại x=2?

A. $y = \frac{2 x + 6}{x^{2} - 2}$

B. $y = \frac{1}{x - 2}$

C. $y = \frac{x}{x + 2}$

D. $y = \frac{3 x - 1}{x - 22}$

Lời giải

Chọn B

Các hàm số ở phương án A, C, D là các hàm phân thức hữu tỉ liên tục trên tập xác định của chúng nên đều liên tục tại x=2.

Câu 11:

Dãy số nào sau đây không phải cấp số nhân?

A.

1; - 1; 1; - 1; 1; - 1

B. $1; 0; 0; 0; 0; 0$

C. $1; 2; 4; 8; 16$

D. $1; 3; 9; 27; 80$

Lời giải

Chọn D

Dãy $1; 3; 9; 27; 80$ không phải cấp số nhân vì $\frac{80}{27} \neq \frac{27}{9}$ .

Câu 12:

Cho a,b là các số dương. Biết $\lim_{x \to - \infty} (\sqrt{9 x^{2} - a x} + \sqrt[3]{27 x^{3} + b x^{2} + 5}) = \frac{7}{27}$ . Tìm giá trị lớn nhất của ab.

A. $\frac{49}{18}$

B. $\frac{59}{34}$

C. $\frac{43}{58}$

D. $\frac{75}{68}$

Lời giải

Chọn A

Ta có $\lim_{x \to - \infty} (\sqrt{9 x^{2} - a x} + \sqrt[3]{27 x^{3} + b x^{2} + 5}) = \lim_{x \to - \infty} (\sqrt{9 x^{2} - a x} + 3 x - 3 x + \sqrt[3]{27 x^{3} + b x^{2} + 5})$ $= \lim_{x \to - \infty} (\frac{- a x}{\sqrt{9 x^{2} - a x} - 3 x} - \frac{- b x^{2} - 5}{9 x^{2} + 3 x \sqrt[3]{27 x^{3} + b x^{2} + 5} + {(\sqrt[3]{27 x^{3} + b x^{2} + 5})}^{2}})$

$= \lim_{x \to - \infty} (\frac{- a x}{- x \sqrt{9 - \frac{a}{x}} - 3 x} - \frac{- b - \frac{5}{x^{2}}}{9 + 3 \sqrt[3]{27 + \frac{b}{x} + \frac{5}{x^{3}}} + {(\sqrt[3]{27 + \frac{b}{x} + \frac{5}{x^{3}}})}^{2}})$

$= \lim_{x \to - \infty} (\frac{a}{\sqrt{9 - \frac{a}{x}} + 3} - \frac{- b - \frac{5}{x^{2}}}{9 + 3 \sqrt[3]{27 + \frac{b}{x} + \frac{5}{x^{3}}} + {(\sqrt[3]{27 + \frac{b}{x} + \frac{5}{x^{3}}})}^{2}})$ . $= \frac{a}{6} + \frac{b}{27}$

Theo đề ta có $\frac{7}{27} = \frac{a}{6} + \frac{b}{27} \geq 2 \sqrt{\frac{a}{6} . \frac{b}{27}} \Rightarrow a b \leq \frac{49}{18}$ .

Dấu đẳng thức xảy ra khi $\frac{a}{6} = \frac{b}{27} = \frac{7}{54} \Leftrightarrow \{\begin{cases} a = \frac{7}{9} \\ b = \frac{7}{2} \end{cases}$ .

Câu 13:

Tính giới hạn

I = \lim_{x \to 1} (\frac{x^{2} - 4 x + 7}{x + 1})

A. I=4

B. I=5

C. I=-4

D. I=2

Lời giải

Chọn D

$I = \lim_{x \to 1} (\frac{x^{2} - 4 x + 7}{x + 1}) = \frac{4}{2} = 2$ .

Câu 14:

Cho hình chóp SABC có đáy ABC là tam giác vuông cân tại B, AB=a. SA vuông góc với mặt phẳng (ABC) và SA=a. Gọi $α$ là góc giữa SB và (SAC). Tính $α$ .

A. $α = 30 °$

B. $α = 60 °$

C. $α = 45 °$

D. $α = 90 °$

Lời giải

Chọn B

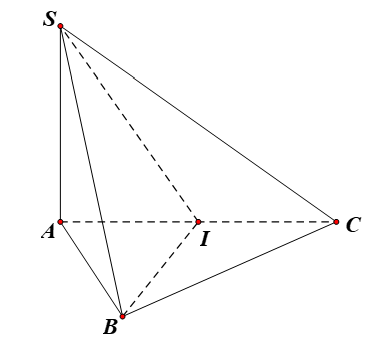
Media VietJack

Từ B kẻ đường thẳng $B I ⊥ A C$ . Lại có $B I ⊥ S A$ nên $B I ⊥ (S A C)$ .

Do đó hình chiếu của SB lên (SAC) là SI, góc giữa SB và (SAC) là góc giữa SB và SI.

Xét tam giác SBI vuông tại I, có $S B = \sqrt{S A^{2} + A B^{2}} = \sqrt{2}$ , $B I = \frac{1}{2} A C = \frac{a \sqrt{2}}{2}$ .

Suy ra $\sin B S I = \frac{B I}{S B} = \frac{1}{2}$ . Vậy $α = 60 °$ .

Câu 15:

Chọn mệnh đề sai

A. $\lim \frac{3}{n + 1} = 0$

B. $\lim {(- 2)}^{n} = + \infty$

C. $\lim (\sqrt{n^{2} + 2 n + 3} - n) = 1$

D. $\lim \frac{1}{2^{n}} = 0$

Lời giải

Chọn B

$\lim {(- 2)}^{n}$ không tồn tại.

Câu 16:

Xét các mệnh đề sau

(I) $\lim n^{k} = + \infty$ với k là số nguyên dương tuỳ ý.

(II) $\lim_{x \to + \infty} \frac{1}{x^{k}} = 0$ với k là số nguyên dương tuỳ ý.

(III) $\lim_{x \to - \infty} x^{k} = + \infty$ với k là số nguyên dương tuỳ ý.

Trong ba mệnh đề trên thì

A. Cả (I),(II),(III) đều đúng.

B. Chỉ (I) đúng.

C. Chỉ (I),(II) đúng.

D. Chỉ (III) đúng.

Lời giải

Chọn C

Ta có: (I),(II) đúng (các giới hạn đặc biệt: SGK trang 114 và trang 130).

Với k là số nguyên dương lẻ tuỳ ý ta có $\lim_{x \to - \infty} x^{k} = - \infty$ (các giới hạn đặc biệt: SGK trang 130)

nên (III)sai .

Câu 17:

Cho biết $\lim_{x \to - \infty} \frac{1 - \sqrt{4 x^{2} - x + 5}}{a |x| + 2} = \frac{2}{3}$ . Giá trị của a bằng

A. 3

B. $\frac{- 2}{3}$

C. -3

D. $\frac{4}{3}$

Lời giải

Chọn C

$\lim_{x \to - \infty} \frac{1 - \sqrt{4 x^{2} - x + 5}}{a |x| + 2} = \lim_{x \to - \infty} \frac{1 + x \sqrt{4 - \frac{1}{x} + \frac{5}{x^{2}}}}{- a x + 2}$ $= \lim_{x \to - \infty} \frac{\frac{1}{x} + \sqrt{4 - \frac{1}{x} + \frac{5}{x^{2}}}}{- a + \frac{2}{x}}$ $= \frac{\sqrt{4}}{- a}$ $= - \frac{2}{a}$ .

Theo giả thiết, ta có: $- \frac{2}{a} = \frac{2}{3}$ $\Leftrightarrow a = - 3$ .

Câu 18:

Tìm tất cả các giá trị của tham số thực m để B>2 với $B = \lim_{x \to 1} (x^{3} - 2 x + 2 m^{2} - 5 m + 5)$ .

A. $m \in \{0; 3\}$

B. $m < \frac{1}{2}$ hoặc $m > 2$

C. $\frac{1}{2} < m < 2$

D. $- 2 < m < 3$

Lời giải

Chọn B

Ta có: $B = \lim_{x \to 1} (x^{3} - 2 x + 2 m^{2} - 5 m + 5)$ $= 1^{3} - 2 + 2 m^{2} - 5 m + 5$ $= 2 m^{2} - 5 m + 4$ .

Theo giả thiết: $B > 2 \Leftrightarrow$ $2 m^{2} - 5 m + 4 > 2$ $\Leftrightarrow 2 m^{2} - 5 m + 2 > 0$ $\Leftrightarrow [\begin{array}{l} m > 2 \\ m < \frac{1}{2} \end{array}$ .

Câu 19:

Kết quả của giới hạn

I = \lim (- 3 n^{2} + 2 n - 4)

A. $+ \infty$

B. $- \infty$

C. 1

D. 0

Lời giải

Chọn B

Ta có: $I = \lim (- 3 n^{2} + 2 n - 4)$ $= \lim [n^{2} (- 3 + \frac{2}{n} - \frac{4}{n^{2}})]$ $= - \infty$ .

Vì $\{\begin{cases} \lim n^{2} = + \infty \\ \lim (- 3 + \frac{2}{n} - \frac{4}{n^{2}}) = - 3 < 0 \end{cases}$ .

Câu 20:

Cho $\lim_{x \to 1} (\frac{\sqrt{x^{2} + x + 2} - \sqrt[3]{2 x^{3} + 5 x + 1}}{x^{2} - 1}) = \frac{a}{b}$ ( $\frac{a}{b}$ là phân số tối giản và a,b nguyên). Tính tổng $L = a^{2} + b^{2}$ .

A. 150

B. 143

C. 140

D. 145

Lời giải

Chọn D

Ta có: $\lim_{x \to 1} (\frac{\sqrt{x^{2} + x + 2} - \sqrt[3]{2 x^{3} + 5 x + 1}}{x^{2} - 1})$ $= \lim_{x \to 1} (\frac{\sqrt{x^{2} + x + 2} - 2}{x^{2} - 1} + \frac{2 - \sqrt[3]{2 x^{3} + 5 x + 1}}{x^{2} - 1})$

$= \lim_{x \to 1} \{\frac{x^{2} + x - 2}{(x^{2} - 1) (\sqrt{x^{2} + x + 2} + 2)} + \frac{- 2 x^{3} - 5 x + 7}{(x^{2} - 1) [4 + 2 \sqrt[3]{2 x^{3} + 5 x + 1} + {(\sqrt[3]{2 x^{3} + 5 x + 1})}^{2}]}\}$

$= \lim_{x \to 1} \{\frac{(x - 1) (x + 2)}{(x - 1) (x + 1) (\sqrt{x^{2} + x + 2} + 2)} + \frac{(x - 1) (- 2 x^{2} - 2 x - 7)}{(x - 1) (x + 1) [4 + 2 \sqrt[3]{2 x^{3} + 5 x + 1} + {(\sqrt[3]{2 x^{3} + 5 x + 1})}^{2}]}\}$

$= \lim_{x \to 1} \{\frac{x + 2}{(x + 1) (\sqrt{x^{2} + x + 2} + 2)} + \frac{- 2 x^{2} - 2 x - 7}{(x + 1) [4 + 2 \sqrt[3]{2 x^{3} + 5 x + 1} + {(\sqrt[3]{2 x^{3} + 5 x + 1})}^{2}]}\}$

$= \frac{3}{2.4} - \frac{11}{2.12}$ $= - \frac{1}{12}$ .

Theo giả thiết ta có $- \frac{1}{12} = \frac{a}{b}$ $\Rightarrow \{\begin{cases} a = - 1 \\ b = 12 \end{cases}$ $\Rightarrow L = a^{2} + b^{2} = 145$ .

Câu 21:

Cho hình lập phương ABCDEFGH có cạnh bằng a. Tích $\vec{A C} . \vec{E F}$

A. $2 a^{2}$

B. $a \sqrt{2}$

C. $\frac{a^{2} \sqrt{2}}{2}$

D. $a^{2}$

Lời giải

Chọn D

Media VietJack

Ta có $\vec{A C} . \vec{E F} = \vec{A C} . \vec{A B} = {\vec{A B}}^{2} = A B^{2} = a^{2}$ .

Câu 22:

Trong không gian cho điểm O và đường thẳng d. Qua điểm O có bao nhiêu mặt phẳng vuông góc với đường thẳng d?

A. Ba

B. Hai

C. Một

D. Vô số

Lời giải

Chọn C

Theo lý thuyết, chỉ có duy nhất một mặt phẳng đi qua điểm O cho trước và vuông góc với đường thẳng d cho trước.

Câu 23:

Cho hình chóp SABC có

S A = S B

A C = C B

. Khẳng định nào sau đây đúng?

A. $B C ⊥ (S A C)$

B. $S B ⊥ A B$

C. $S A ⊥ (A B C)$

D. $A B ⊥ S C$

Lời giải

Chọn D

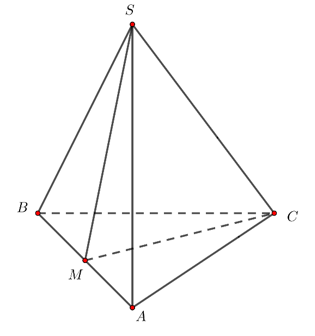
Media VietJack

Gọi M là trung điểm AB, do hai tam giác SAB và CAB cân có chung đáy AB nên $\{\begin{cases} A B ⊥ S M \\ A B ⊥ C M \end{cases} \Rightarrow A B ⊥ (S M C) \Rightarrow A B ⊥ S C$ .

Câu 24:

Tính giới hạn

L = \lim_{x \to + \infty} \frac{2 x - 3}{- 4 x + 2}

A. L=1

B. $L = \frac{1}{2}$

C. $L = \frac{- 1}{2}$

D. $L = \frac{- 3}{4}$

Lời giải

Chọn C

Ta có $L = \lim_{x \to + \infty} \frac{2 x - 3}{- 4 x + 2} = \lim_{x \to + \infty} \frac{2 - \frac{3}{x}}{- 4 + \frac{2}{x}} = - \frac{1}{2}$ .

Câu 25:

Cho hai đường thẳng a,b phân biệt và mặt phẳng (P). Mệnh đề nào sau đây đúng?

A. Nếu $a // (P)$ và $b ⊥ a$ thì $b ⊥ (P)$ . B. Nếu $a ⊥ (P)$ và $b ⊥ a$ thì $b // (P)$ .

C. Nếu $a // (P)$ và $b ⊥ (P)$ thì $b ⊥ a$ . D. Nếu $a // (P)$ và $b // (P)$ $b // a$ thì .

B. Nếu

a ⊥ (P)

và

b ⊥ a

thì

b // (P)

.

C. Nếu

a // (P)

và

b ⊥ (P)

thì

b ⊥ a

D. Nếu

a // (P)

và

b // (P)

thì

a / / b

Chọn C

Câu 26:

Tính giới hạn $\lim (2 + \frac{1}{2} + \frac{1}{4} + \frac{1}{8} + ... + \frac{1}{2^{n}} + ...) .$

A. 4

B. 3

C. 5

D. $\frac{4}{3}$

Lời giải

Chọn B.

Ta có $\frac{1}{2} + \frac{1}{4} + \frac{1}{8} + ... + \frac{1}{2^{n}} + ...$ là một cấp số nhân lùi vô hạn với $u_{1} = \frac{1}{2}, q = \frac{1}{2}$ nên

$S_{n} = \frac{1}{2} + \frac{1}{4} + \frac{1}{8} + ... + \frac{1}{2^{n}} + ... = \frac{\frac{1}{2}}{1 - \frac{1}{2}} = 1.$

Nên $\lim (2 + \frac{1}{2} + \frac{1}{4} + \frac{1}{8} + ... + \frac{1}{2^{n}} + ...) = \lim 2 + \lim (\frac{1}{2} + \frac{1}{4} + \frac{1}{8} + ... + \frac{1}{2^{n}} + ...) = 2 + 1 = 3.$

Câu 27:

Tính giới hạn $I = \lim (\sqrt{n^{2} - 4 n + 8} - n) .$

A. $+ \infty$

B. 0

C. -2

D. 1

Lời giải

Chọn C.

Ta có $I = \lim (\sqrt{n^{2} - 4 n + 8} - n) = \lim \frac{(\sqrt{n^{2} - 4 n + 8} - n) (\sqrt{n^{2} - 4 n + 8} + n)}{\sqrt{n^{2} - 4 n + 8} + n} = \lim \frac{- 4 n + 8}{\sqrt{n^{2} - 4 n + 8} + n}$ .

$= \lim \frac{n (- 4 + \frac{8}{n})}{n \sqrt{1 - \frac{4}{n} + \frac{8}{n^{2}}} + n} = \lim \frac{- 4 + \frac{8}{n}}{\sqrt{1 - \frac{4}{n} + \frac{8}{n^{2}}} + 1} = \frac{- 4}{2} = - 2.$

Câu 28:

Cho hình chóp SABC có đáy là tam giác ABC vuông tại B và SA vuông góc với mặt phẳng ABC. Mệnh đề nào sai ?

A. $B C ⊥ S A$

B. $B C ⊥ (S A B)$

C. $B C ⊥ S B$

D. $B C ⊥ (S A C)$

Lời giải

Chọn D

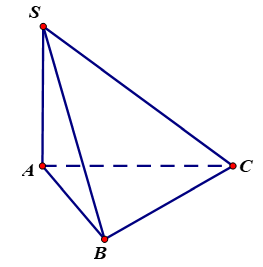
Media VietJack

Ta có $\{\begin{cases} B C ⊥ A B ( gt) \\ B C ⊥ S A ( gt) \end{cases} \Rightarrow B C ⊥ (S A B) \Rightarrow B C ⊥ S B$ .

Mệnh đề ở câu D sai.

Câu 29:

Giá trị $\lim_{x \to - \infty} \frac{\sqrt{x^{2} - 3 x + 6} + 2 x}{2 x - 3}$ bằng

A. $\frac{1}{2}$

B. $\frac{9}{17}$

C. $\frac{3}{2}$

D. 1

Lời giải

Chọn A

$\lim_{x \to - \infty} \frac{\sqrt{x^{2} - 3 x + 6} + 2 x}{2 x - 3} = \lim_{x \to - \infty} \frac{- x \sqrt{1 - \frac{3}{x} + \frac{6}{x^{2}}} + 2 x}{2 x - 3} = \lim_{x \to - \infty} \frac{- \sqrt{1 - \frac{3}{x} + \frac{6}{x^{2}}} + 2}{2 - \frac{3}{x}} = \frac{1}{2}$ .

Câu 30:

Tính giới hạn

I = \lim \frac{2 n^{2} - 3 n + 5}{2 n + n^{2}}

A. 1

B. $\frac{- 3}{2}$

C. 0

D. 2

Lời giải

Chọn D

$I = \lim \frac{2 n^{2} - 3 n + 5}{2 n + n^{2}} = \lim \frac{2 - \frac{3}{n} + \frac{5}{n^{2}}}{\frac{2}{n} + 1} = 2$ .

Câu 31:

Cho dãy số $u_{n}$ với $u_{n} = 3 n + 2$ . Tìm số hạng thứ 5 của dãy số

A. 7

B. 15

C. 17

D. 5

Lời giải

Chọn C

Ta có $U_{n}$ là cấp số cộng có công sai $d = 3, u_{1} = 5$ nên $u_{5} = u_{1} + 4 d = 5 + 4.3 = 17$ .

Câu 32:

Tính giới hạn

I = \lim \frac{2 n (3 - n) + 1}{1 + 3 + 5 + ... + (2 n - 1)}

A. 2

B. 1

C. -2

D. -3

Lời giải

Chọn C

Ta có $1 + 3 + 5 + ... + (2 n - 1) = n^{2}, \forall n \in ℕ^{*} .$

$I = \lim \frac{2 n (3 - n) + 1}{1 + 3 + 5 + ... + (2 n - 1)} = \lim \frac{- 2 n^{2} + 6 n + 1}{n^{2}}$ $= \lim (- 2 + \frac{6}{n} + \frac{1}{n^{2}}) = - 2$ .

Câu 33:

Cho hình chóp SABCD có đáy là hình thoi O, SO vuông góc với mặt phẳng đáy. Gọi $α$ là góc giữa đường thẳng SD và mặt phẳng đáy.

A. $α = \hat{S D A}$

B. $α = \hat{S D O}$

C. $α = \hat{S A D}$

D. $α = \hat{A S D}$

Lời giải

Chọn B

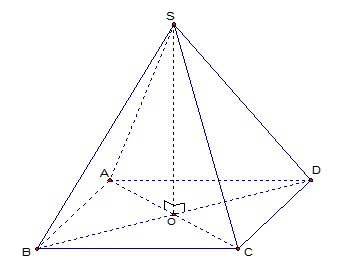
Cho hình chóp SABCDcó đáy là hình thoi O, SO vuông góc với mặt phẳng đáy. Gọi anpha là góc giữa đường thẳng SD và mặt phẳng đáy. (ảnh 1)

Ta có OD là hình chiếu của SD lên mặt phẳng (ABCD)

Góc giữa SD và mặt đáy (ABCD) là góc giữa hai đường thẳng SD và OD.

$Δ S D O$ vuông tại $O \Rightarrow (\hat{S D, O D}) = \hat{S D O}$ .

Câu 34:

y = \sin x (I), y = \cos \sqrt{x} (I I), y = \tan x (I I I)

số . Hàm số nào liên tục trên R.

A. (I), (II)

B. (I)

C. (I), (II), (III)

D. (III)

Lời giải

Chọn B

Hàm số $y = \sin x$ có tập xác định là D=R nên liên tục trên R.

Hàm số $y = \cos \sqrt{x}$ có tập xác định $D = [0; + \infty)$ , liên tục trên $[0; + \infty)$ .

Hàm số $y = \tan x$ liên tục tại mọi điểm $x \neq \frac{π}{2} + k π, k \in ℤ$ .

Câu 35:

\lim_{x \to 2} f (x) = 5

\lim_{x \to 2} [3 - 4 f (x)]

bằng bao nhêu?

A. -18

B. -1

C. 1

D. -17

Lời giải

Chọn D

Ta có

Vì $\lim_{x \to 2} f (x) = 5$ hữu hạn nên $\lim_{x \to 2} [3 - 4 f (x)] = \lim_{x \to 2} 3 - 4. \lim_{x \to 2} f (x) = 3 - 4.5 = - 17.$

Câu 36:

Cho hình lăng trụ ABCA'B'C'. Đặt $\vec{A A^{'}} = \vec{a}$ , $\vec{A B} = \vec{b}$ , $\vec{A C} = \vec{c}$ . Phân tích véc tơ $\vec{B C'}$ qua các véc tơ $\vec{a}, \vec{b}, \vec{c}$

A. $\vec{B C'} = \vec{a} - \vec{b} + \vec{c}$

B. $\vec{B C'} = \vec{a} + \vec{b} + \vec{c}$

C. $\vec{B C'} = \vec{a} + \vec{b} - \vec{c}$

D. $\vec{B C'} = \vec{a} - \vec{b} - \vec{c}$

Chọn A

Cho hình lăng trụ ABCA'B'C' Đặt vectơ AA'=vectơ a, vectơ AB= vectơ b ,vectơ AC= vectơ AC . (ảnh 1)

Có $\vec{B C^{'}} = \vec{B C} + \vec{B B^{'}} = \vec{A A^{'}} + \vec{B A} + \vec{A C} = \vec{a} - \vec{b} + \vec{c}$

Câu 37:

Cho điểm O ở ngoài mặt phẳng $(α)$ . Trong mặt phẳng $(α)$ có đường thẳng d di động qua điểm A cố định . Gọi H,M lần lượt là hình chiếu của O trên mặt phẳng $(α)$ và đường thẳng d. Độ dài đoạn OM lớn nhất khi

A. Đường thẳng d trùng với HA.

B. Đường thẳng d tạo với HA một góc

45 °

C. Đường thẳng d tạo với HA một góc

60 °

.

D. Đường thẳng d vuông góc với HA.

Lời giải

Chọn D

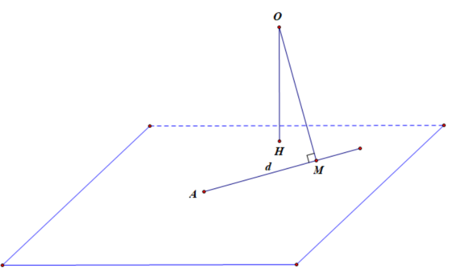
Media VietJack

Có $O M \leq O A$ nên $O M_{\max} = O A$ khi $M \equiv A \Rightarrow O A ⊥ d \Rightarrow d ⊥ H A$ .

Câu 38:

Cho hàm số $f (x) = \{\begin{cases} \frac{\sqrt{1 + 2 x} - 1}{x} k h i x > 0 \\ 1 + 3 x k h i x \leq 0 \end{cases}$ . Mệnh đề nào sau đây đúng ?

A. Hàm số liên tục trên R.

B. Hàm số gián đoạn tại x=3.

C. Hàm số gián đoạn tại x=0.

D. Hàm số gián đoạn tại x=1

Lời giải

Chọn B

Xét tính liên tục của hàm số tại x=0.

f(x)=0.

$\lim_{x \to 0^{+}} f (x) = \lim_{x \to 0^{+}} \frac{\sqrt{1 + 2 x} - 1}{x} = \lim_{x \to 0^{+}} \frac{2 x}{x (\sqrt{1 + 2 x} + 1)} = 1$ .

$\lim_{x \to 0^{-}} f (x) = \lim_{x \to 0^{-}} (1 + 3 x) = 1$ nên hàm số liên tục tại x=0.

Vậy hàm số liên tục trên R.

Câu 39:

Cho hình chóp SABCD có đáy ABCD hình thang vuông tại A và D. $A B = A D = a, C D = 2 a$ , SD vuông góc với mặt phẳng (ABCD). Có bao nhiêu mặt bên của hình chóp là tam giác vuông.

A. 1

B. 2

C. 3

D. 4

Lời giải

Chọn D

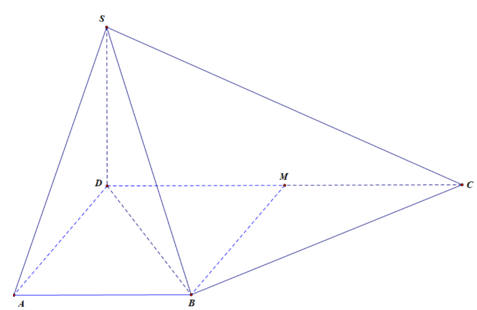
Cho hình chóp SABCD có đáy ABCD hình thang vuông tại A và D (ảnh 1)

$Δ S D C, Δ S D A$ là các tam giác vuông.

$A B ⊥ A D, A B ⊥ S D \Rightarrow A B ⊥ (S A D) \Rightarrow Δ S A B$ vuông.

Gọi M là trung điểm $C D \Rightarrow B C ⊥ B D \Rightarrow B C ⊥ (S B D) \Rightarrow Δ S B C$ vuông.

Câu 40:

Biết bốn số $6; x; - 2; y$ theo thứ tự lập thành cấp số cộng. Giá trị của biểu thức x+2y bằng.

A. -10

B. 12

C. 14

D. 2

Lời giải

Chọn C.

Do bốn số $6; x; - 2; y$ theo thứ tự lập thành cấp số cộng suy ra $\{\begin{cases} 6 - 2 = 2 x \\ x + y = - 4 \end{cases} \Leftrightarrow \{\begin{cases} x = 2 \\ y = 6 \end{cases} \Rightarrow x + 2 y = 14$ .

Câu 41:

Chọn mệnh đề đúng

A. $\lim \frac{2 n^{2} + n - 1}{3 - 2 n} = - \infty$

B. $\lim (3 n^{2} - n^{3} + 1) = + \infty$

C. $\lim \frac{1 - 3 n}{2 n + 5} = \frac{1}{2}$

D. $\lim 2^{n} = 0$

Chọn A

Ta có $\lim \frac{2 n^{2} + n - 1}{3 - 2 n} = \lim n (\frac{2 + \frac{1}{n} - \frac{1}{n^{2}}}{\frac{3}{n} - 2}) = - \infty$

Câu 42:

Cho hình chóp SABC có SA=SB=SC và tam giác ABC vuông tại C. Gọi H là hình chiếu của S trên mặt phẳng (ABC). Khẳng định nào sau đây đúng ?

A. H trùng với trọng tâm của tam giác ABC.

B. H trùng với trung điểm của AB.

C. H trùng với trực tâm của tam giác ABC.

D. H trùng với trung điểm của BC.

Lời giải

Chọn B

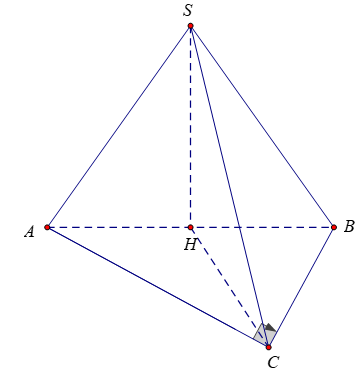
Media VietJack

Do $S A = S B = S C$ và H là hình chiếu của S trên mặt phẳng (ABC) nên $H A = H B = H C$ . Suy ra H là tâm đường tròn ngoại tiếp tam giác ABC mà tam giác ABC vuông tại C. Khi đó H trùng với trung điểm của AB.

Câu 43:

Cho tứ diện đều ABCD. Tính góc giữa các véc tơ $\vec{D A}$ và $\vec{B D}$

A. $60 °$

B. $90 °$

C. $30 °$

D. $120 °$

Lời giải

Chọn D

Cho tứ diện đều ABCD. Tính góc giữa các véc tơ vectơ DA và vectơ BD (ảnh 1)

Vẽ $\vec{D E} = \vec{B D}$ khi đó $\hat{(\vec{D A}; \vec{B D})} = \hat{(\vec{D A}; \vec{D E})} = \hat{A D E}$ $\Rightarrow \hat{(\vec{D A}; \vec{B D})} = 120^{0}$ .

Câu 44:

Cho hàm số $f (x) = \{\begin{cases} 1 + \cos x khi \sin x \geq 0 \\ 3 - \cos x khi \sin x < 0 \end{cases}$

Hàm số có bao nhiêu điểm gián đoạn trên khoảng (0,2019)?

A. Vô số

B. 320

C. 321

D. 319

Lời giải

Chọn C

Xét hàm số f(x) trên đoạn $[0; 2 π]$ , khi đó

$f (x) = \{\begin{cases} 1 + \cos x khi x \in [0; π] \\ 3 - \cos x khi x \in (π; 2 π) \end{cases}$

Ta có $\lim_{x \to 0^{+}} f (x) = 2 = f (0)$ , $\lim_{x \to {(2 π)}^{-}} f (x) = 2 = f (2 π)$

$\lim_{x \to π^{-}} f (x) = \lim_{x \to π^{-}} (1 + \cos x) = 0$ , $\lim_{x \to π^{+}} f (x) = \lim_{x \to π^{+}} (3 - \cos x) = 4$

do $\lim_{x \to π^{-}} f (x) \neq \lim_{x \to π^{+}} f (x)$ nên hàm số gián đoạn tại $x = π$ . Hàm số $y = \cos x$ tuần hoàn

với chu kỳ $2 π$ . Suy ra hàm số gián đoạn tại các điểm $x = π + k 2 π$ với $k \in Z$ .

Ta có $x \in (0; 2019)$ $\Leftrightarrow 0 < π + k 2 π < 2019 \Leftrightarrow - \frac{1}{2} < k < 320, 833$ với $k \in Z$

nên $k \in \{0; 1; 2; ....; 320\}$ . Vậy hàm số có 321 điểm gián đoạn.

Câu 45:

Cho hàm số $f (x) = \{\begin{cases} \frac{2 x^{2} + 3 x - 2}{x + 2} khi x \neq - 2 \\ m^{2} + m x - 8 khi x = - 2 \end{cases}$ Tìm tổng các giá trị tìm được của tham số m để hàm số liên tục tại x=-2.

A. 2

B. 4

C. 1

D. 5

Chọn A

Lời giải

Ta có $\lim_{x \to - 2} \frac{2 x^{2} + 3 x - 2}{x + 2} = \lim_{x \to - 2} (2 x - 1) = - 5$ , $f (- 2) = m^{2} - 2 m - 8$ . Để hàm số liên tục

tại $x = - 2 \Leftrightarrow$ $\lim_{x \to 2} f (x) = f (2) \Leftrightarrow$ $m^{2} - 2 m - 8 = - 5$ $\Leftrightarrow [\begin{array}{l} m = 3 \\ m = - 1 \end{array}$

Suy ra tổng các giá trị tìm được của tham số m để hàm số liên tục tại x=-2 là: 2

Câu 46:

Cho hàm số y= f(x) liên tục trên đoạn [1,5] và $f (1) = 2$ , $f (5) = 10$ . Khẳng định nào sau đây ĐÚNG?

A. Phương trình $f (x) = 6$ vô nghiệm.

B. Phương trình

f (x) = 7

có ít nhất một nghiệm trên (1,5).

C. Phương trình

f (x) = 2

có hai nghiệm x=1 và x=5.

D. Phương trình

f (x) = 7

vô nghiệm.

Lời giải

Chọn B.

Hàm số liên tục trên đoạn [1,5] và $f (1) = 2$ , $f (5) = 10$ , $7 \in (2; 10)$ nên theo định lý giá trị trung bình ta có $\exists x_{0} \in (1; 5) : f (x_{0}) = 7$ hay phương trình $f (x) = 7$ có ít nhất một nghiệm trên (1,5).

Câu 47:

Cho hình chóp ABCD có đáy là hình vuông tâm O, cạnh đáy bằng a. Cạnh SA vuông góc với đáy và $S A = a \sqrt{3}$ . Gọi $(α)$ là mặt phẳng chứa B và vuông góc với SB. Tính diện tích thiết diện tạo bởi hình chóp trên và $(α)$ .

A. $\frac{a^{2} \sqrt{15}}{10}$

B. $\frac{a^{2} \sqrt{15}}{5}$

C. $\frac{a^{2} \sqrt{15}}{20}$

D. $\frac{a^{2} \sqrt{5}}{10}$

Lời giải

Chọn A.

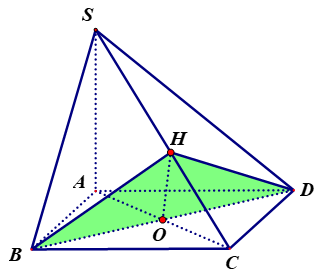
Do $S C ⊥ (α)$ và dễ dàng chứng minh $B D ⊥ S C$ , nên suy ra $B D \subset (α)$ .

Kẻ $B H ⊥ S C t h ì B H \subset (α)$ .

Vậy thiết diện là $Δ B D H$ .

Với tam giác $Δ S B C$ vuông tại B ta có $B H = \frac{B C . B S}{S C} = \frac{B C . B S}{\sqrt{B C^{2} + B S^{2}}} = \frac{2 a}{\sqrt{5}}$ .

Có $B O = \frac{a \sqrt{2}}{2} \Rightarrow H O = a \sqrt{\frac{3}{10}}$

Mà tam giác $Δ B D H$ cân tại H $\Rightarrow S_{Δ B D H} = B O . H O = a^{2} \sqrt{\frac{3}{20}} = a^{2} \frac{\sqrt{15}}{10}$

Câu 48:

\lim_{x \to 1} \frac{f (x) + 1}{x - 1} = - 1

I = \lim_{x \to 1} \frac{(x^{2} + x) f (x) + 2}{x - 1}

A. 5

B. -4

C. 4

D. -5

Lời giải

Chọn D.

$I = \lim_{x \to 1} \frac{(x^{2} + x) f (x) + 2}{x - 1} = \lim_{x \to 1} [\frac{f (x) + 1}{x - 1} (x^{2} + x) + \frac{- x^{2} - x + 2}{x - 1}]$

Mà $\lim_{x \to 1} \frac{f (x) + 1}{x - 1} = - 1 \lim_{x \to 1} (x^{2} + x) = 2$ ,

$\lim_{x \to 1} \frac{- x^{2} - x + 2}{x - 1} = \lim_{x \to 1} \frac{(- x - 2) (x - 1)}{x - 1} = \lim_{x \to 1} (- x - 2) = - 3$

nên $I = - 1.2 - 3 = - 5$ .

Câu 49:

\lim_{x \to - 2} \frac{\sqrt{2 x {}^{2}+ x + 3} - 3}{4 - x {}^{2}}

A. $\frac{- 2}{7}$

B. $\frac{- 7}{24}$

C. $\frac{- 9}{31}$

D. 0

Lời giải

Chọn B.

$\lim_{x \to - 2} \frac{\sqrt{2 x {}^{2}+ x + 3} - 3}{4 - x {}^{2}}$ $= \lim_{x \to - 2} \frac{(x + 2) (2 x - 3)}{(2 - x) (2 + x) (\sqrt{2 x {}^{2}+ x + 3} + 3)}$ $= \lim_{x \to - 2} \frac{(2 x - 3)}{(2 - x) (\sqrt{2 x {}^{2}+ x + 3} + 3)}$ $= \frac{- 7}{24}$

Câu 50:

Hàm số $y = \frac{x + 1}{x^{2} + 7 x + 12}$ liên tục trên khoảng nào sau đây?

A. (3,4)

B. $(- \infty; 4)$

C. (-4,3)

D. $(- 4; + \infty)$

Lời giải

Chọn A.

Tập xác định của hàm số là $D = (- \infty; - 4) \cup (- 3; + \infty) \Rightarrow D \supset (3; 4)$

Vậy hàm số liên tục trên (3,4).

Bắt đầu thi ngay

Bài thi liên quan

Có thể bạn quan tâm

Các bài thi hot trong chương