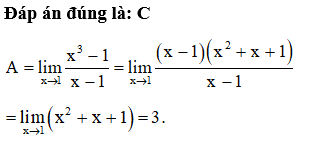25 câu hỏi trắc nghiệm thuộc Đề kiểm tra Giữa kì 2 Toán 11 có đáp án (Mới nhất) (Đề 11)

Câu 1:

Cho cấp số nhân (u_n), biết u₁ = 1; u₄ = 64. Tính công bội q của cấp số nhân.

A. q = 4;

B. q = ±4;

C. q = 21;

D. $q = 2 \sqrt{2} .$

Xem đáp án

Đáp án đúng là: A

Cho cấp số nhân (u_n) có số hạng tổng quát là u_n = u₁.qⁿ^-¹.

u₁ = 1; u₄ = 64 nên ta có hệ phương trình

$\{\begin{matrix} u_{1} = 1 \\ u_{1} . q^{3} = 64 \end{matrix} \Rightarrow q^{3} = 64 \Rightarrow q = 4.$

Câu 2:

Dãy số nào sau đây có giới hạn bằng 0?

A. $u_{n} = \frac{n^{3} - 3 n}{n + 1};$

B. $u_{n} = {(\frac{- 2}{3})}^{n};$

C. $u_{n} = {(\frac{6}{5})}^{n};$

D. u_n = n² - 4n.

Xem đáp án

Dãy số nào sau đây có giới hạn bằng 0? (ảnh 1)

Câu 3:

Tính $I = \lim [n (\sqrt{n^{2} + 2} - \sqrt{n^{2} - 1})] .$

A. I = +¥;

B. I = 0;

C. I = 1,499;

D. $I = \frac{3}{2} .$

Xem đáp án

. Tính I= lim n(căn n^2+2- căn n^2-1 (ảnh 1)

Câu 4:

Cho một cấp số cộng (u_n) có $u_{1} = \frac{1}{3}$ , u₈ = 26. Tìm công sai d.

A. $d = \frac{3}{11};$

B. $d = \frac{10}{3};$

C. $d = \frac{3}{10};$

D. $d = \frac{11}{3} .$

Xem đáp án

Đáp án đúng là: D

Công thức tổng quát các số hạng của cấp số cộng (u_n) là u_n = u₁ + (n - 1).d

Ta có: , u₈ = 26 nên ta có hệ phương trình

$\{\begin{matrix} u_{1} = \frac{1}{3} \\ u_{1} + 7 d = 26 \end{matrix} \Rightarrow 7 d = \frac{77}{3} \Leftrightarrow d = \frac{11}{3} .$

Câu 5:

Cho hình chóp S.ABC có SA = SB = SC và tam giác ABC vuông tại B. Vẽ SH ^ (ABC), H Î (ABC). Khẳng định nào sau đây đúng?

A. H trùng với trực tâm tam giác ABC;

B. H trùng với trọng tâm tam giác ABC;

C. H trùng với trung điểm AC;

D. H trùng với trung điểm BC.

Xem đáp án

Đáp án đúng là: C

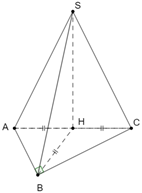
Cho hình chóp S.ABC có SA = SB = SC và tam giác ABC vuông tại B. Vẽ SH  (ABC), H  (ABC). Khẳng định nào sau đây đúng? (ảnh 1)

Kẻ SH ^ (ABC)

Áp dụng định lý Pytago vào các tam giác vuông SHA, SHB, SHC

$A H = \sqrt{S A^{2} - S H^{2}} B H = \sqrt{S B^{2} - S H^{2}} C H = \sqrt{S C^{2} - S H^{2}}$

Mà SA = SB = SC nên ta có AH = BH = CH

Với tam giác ABC vuông tại B thì để thỏa mãn điều kiện AH = BH = CH thì H là trung điểm của AC.

Câu 6:

Xác định x dương để ba số hạng liên tiếp sau: 2x - 3; x; 2x + 3 lập thành một cấp số nhân.

A. x = 3;

B.

x = \sqrt{3};

C. không có giá trị nào của x;

D.

x = \pm \sqrt{3} .

Xem đáp án

Đáp án đúng là: B

Để ba số hạng liên tiếp sau: 2x - 3; x; 2x + 3 lập thành một cấp số nhân.

(2x - 3).(2x + 3) = x²

Û 4x² - 9 = x²

Û x²= 3

$\Rightarrow x = \pm \sqrt{3}$

Mà x dương nên $x = \sqrt{3} .$

Câu 7:

Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SD = a và SD vuông góc với mặt phẳng đáy. Tính góc giữa đường thẳng SA và mặt phẳng (SBD).

A. 45°;

B. 30°;

C.

a r c s i n \frac{1}{4};

D. 60°.

Xem đáp án

Đáp án đúng là: B

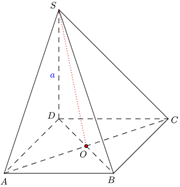
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SD = a và SD vuông góc với mặt phẳng đáy. Tính góc giữa đường thẳng (ảnh 1)

Ta có: Lấy O là giao của AC và BD

SD ^ (ABCD) Þ SD ^ AO

Lại có AO ^ BD.

Nên suy ra AO ^ (SBD).

Góc giữa đường thẳng SA và mặt phẳng (SBD) là góc giữa SA và SO và là a.

Áp dụng định lý Pytago vào hai tam giác vuông SDA và DAB.

$S A = \sqrt{S D^{2} + A D^{2}} = \sqrt{a^{2} + a^{2}} = a \sqrt{2} B D = \sqrt{A B^{2} + A D^{2}} = \sqrt{a^{2} + a^{2}} = a \sqrt{2}$ ;

Tam giác ADB vuông tại A có AO là đường trung tuyến nên:

$A O = \frac{B D}{2} = \frac{a \sqrt{2}}{2} \sin \hat{A S O} = \frac{A O}{S A} = \frac{\frac{a \sqrt{2}}{2}}{a \sqrt{2}} = \frac{1}{2} \Rightarrow \sin α = \frac{1}{2}$

Þ a = 30°.

Câu 8:

Tính $\lim_{x \to 5} \frac{x^{2} - 12 x + 35}{25 - 5 x} .$

A. +¥;

B. -¥;

C.

\frac{2}{5};

D.

- \frac{2}{5} .

Xem đáp án

Tính lim x đến 5 x^2-12x+35/25-5x (ảnh 1)

Câu 9:

Cho dãy số (u_n) là một cấp số cộng có u₁ = 3 và công sai d = 4. Biết tổng n số hạng đầu của dãy số (u_n) là S_n = 253. Tìm n.

A. 9;

B. 12;

C. 11;

D. 10.

Xem đáp án

Đáp án đúng là: C

Công thức tổng quát các số hạng của cấp số cộng (u_n) là u_n = u₁ + (n - 1).d

Þ u_n = 3 + (n - 1).4

Công thức dùng để tính tổng n số hạng đầu của cấp số cộng đã cho là:

. $S_{n} = \frac{n}{2} [2 u_{1} + (n - 1) d] = \frac{n}{2} [2.3 + (n - 1) .4] = \frac{n}{2} [4 n + 2]$

Tổng n số hạng đầu của dãy số (u_n) là

Û 2n² + n = 253

Û 2n² - 22n + 23n - 253 = 0

Û (n - 11).(2n + 23) = 0

$\Leftrightarrow [\begin{matrix} n = 11 \\ n = \frac{- 23}{2} \end{matrix}$

Với n Î ℕ^* nên n = 11.

Câu 10:

Cho hình chóp S.ABCD có đáy ABCD là hình vuông và SA vuông góc đáy. Mệnh đề nào sau đây sai?

A. BD ^ (SAC);

B. AC ^ (SBD);

C. CD ^ (SAD);

D. BC ^ (SAB).

Xem đáp án

Đáp án đúng là: B

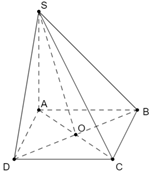
Cho hình chóp S.ABCD có đáy ABCD là hình vuông (ảnh 1)

+) $\begin{matrix} B C ⊥ A B \\ B C ⊥ S A \end{matrix}\} \Rightarrow B C ⊥ (S A B)$ (Phương án D đúng)

+) $\begin{matrix} B D ⊥ A C \\ B D ⊥ S A \end{matrix}\} \Rightarrow B D ⊥ (S A C)$ (Phương án A đúng)

+) $\begin{matrix} D C ⊥ A D \\ D C ⊥ S A \end{matrix}\} \Rightarrow D C ⊥ (S A D)$ (Phương án C đúng)

+) Xét phương án B, giả sử AC ^ (SBD) thì suy ra AC ^ SO (Với O là giao của AC và BD) (1)

Mà SA vuông góc với đáy nên SA vuông góc với AC (2)

Từ (1) và (2) suy ra giả thuyết AC ^ (SBD) là điều vô lý.

Câu 11:

Tính giới hạn $\lim \frac{n^{3} - 2 n}{3 n^{2} + n - 2} .$

A. 0

B. +¥;

C. $\frac{1}{3};$

D. -¥.

Xem đáp án

Tính giới hạn lim n^3-2n/3n^2+n-2 (ảnh 1)

Câu 12:

Cho hai đường thẳng phân biệt a, b và mặt phẳng (a). Mệnh đề nào dưới đây là đúng?

A. Nếu a // (a) và b ^ a thì b ^ (a);

B. Nếu a // (a) và b // (a) thì b // a;

C. Nếu a // (a) và b ^ (a) thì a ^ b;

D. Nếu a ^ (a) và b ^ a thì b // (a).

Xem đáp án

Đáp án đúng là: C

+ Nếu a // (a) và b ^ a thì b ^ (a) (Sai vì b và mặt phẳng (a) còn có thể song song với nhau)

+ Nếu a // (a) và b // (a) thì b // a (Sai vì hai đường thẳng a và b còn có thể vuông góc hoặc chéo nhau)

+ Nếu a // (a) và b ^ (a) thì a ^ b (Đúng)

+ Nếu a ^ (a) và b ^ a thì b // (a) (Sai vì b có thể nằm trong (a)).

Câu 13:

. Cho tứ diện ABCD có AB = AC = 5, DB = DC = 4. Khẳng định nào sau đây đúng?

A. AC ^ BD;

B. AB ^ (BCD);

C. DC ^ (ABC);

D. BC ^ AD.

Xem đáp án

Đáp án đúng là: D

Gọi M là trung điểm của BC.

Xét tam giác ABC có AB = AC = 5 nên tam giác ABC cân tại A.

Xét tam giác DBC có DB = DC = 4 nên tam giác DBC cân tại D.

Hai tam giác cân ABC và tam giác DBC lần lượt cân tại A và D có M là trung điểm của BC nên AM và DM lần lượt là đường cao của hai tam giác này.

Ta có BC ^ AM, BC ^ DM.

Suy ra BC ^ (AMD).

Do đó BC ^ AD (vì AD Ì (AMD)).

Câu 14:

Trong không gian, cho các mệnh đề sau, mệnh đề nào là mệnh đề đúng?

A. Hai đường thẳng cùng vuông góc với đường thẳng thứ ba thì vuông góc với nhau;

B. Hai đường thẳng cùng song song với đường thẳng thứ ba thì song song với nhau;

C. Một đường thẳng vuông góc với một trong hai đường thẳng song song thì vuông góc với đường thẳng còn lại;

D. Một đường thẳng vuông góc với một trong hai đường thẳng vuông góc thì vuông góc với đường thẳng còn lại.

Xem đáp án

Đáp án đúng là: C

+ Hai đường thẳng cùng vuông góc với đường thẳng thứ ba thì vuông góc với nhau (Sai vì hai đường thẳng cùng vuông góc với đường thẳng thứ ba thì chúng song song với nhau).

+ Hai đường thẳng cùng song song với đường thẳng thứ ba thì song song với nhau (Sai vì hai đường thẳng cùng song song với đường thẳng thứ ba thì chúng có thể song song hoặc trùng nhau).

+ Một đường thẳng vuông góc với một trong hai đường thẳng song song thì vuông góc với đường thẳng còn lại (Đúng)

+ Một đường thẳng vuông góc với một trong hai đường thẳng vuông góc thì vuông góc với đường thẳng còn lại (Sai vì một đường thẳng vuông góc với một trong hai đường thẳng vuông góc thì song song với đường thẳng còn lại).

Câu 15:

Cho cấp số nhân (u_n); u₁ = 1, q = 2. Hỏi số 1024 là số hạng thứ mấy?

A. 8;

B. 9;

C. 11;

D. 10.

Xem đáp án

Đáp án đúng là: C

Cho cấp số nhân (u_n) có số hạng tổng quát là u_n = u₁.qⁿ^-¹

Þ u_n = 2ⁿ^-¹

Khi đó u_n = 2ⁿ^-¹ = 1024

Þ n - 1 = log₂ 1024 = 10

Û n = 11

Vậy số 1024 là số hạng thứ 11

Câu 16:

Cho cấp số cộng (u_n) có số hạng tổng quát là u_n = 3n - 2. Tìm công sai d của cấp số cộng.

A. d = 2;

B. d = -2;

C. d = 3;

D. d = -3.

Xem đáp án

Đáp án đúng là: C

Công thức tổng quát các số hạng của cấp số cộng (u_n) là u_n = u₁ + (n - 1).d

Þ u_n = u₁ - d + n.d

Mà u_n = 3n - 2

Þ (u₁ - d) + n.d = 3n - 2

$\Rightarrow \{\begin{matrix} u_{1} - d = - 2 \\ n . d = 3 n \end{matrix} \Leftrightarrow \{\begin{matrix} u_{1} = d - 2 \\ d = 3 \end{matrix} \Leftrightarrow \{\begin{matrix} u_{1} = 1 \\ d = 3 \end{matrix}$