38 câu hỏi trắc nghiệm thuộc Đề kiểm tra Giữa kì 2 Toán 11 có đáp án (Mới nhất) (Đề 4)

Câu 1:

u_{n} = \frac{n^{2}}{n + 1}, \forall n \in ℕ^{*}

. Số hạng đầu tiên của dãy số là:

A. $u_{1} = - \frac{1}{3}$

B. $u_{1} = \frac{4}{3}$

C. $u_{1} = 0$

D. $u_{1} = \frac{1}{2}$

Xem đáp án

Ta có : $u_{1} = \frac{1^{2}}{1 + 1} = \frac{1}{2}$ .

Chọn đáp án D.

Câu 2:

Cho dãy số (u_n), biết

\{\begin{cases} u_{1} = 2 \\ u_{n + 1} = 2 u_{n} - 1 \end{cases}

với

n \geq 1

. Ba số hạng đầu tiên của dãy số đó lần lượt là:

A. 2; 3; 5.

B. 2; 5; 11.

C. –1; 2; 3.

D. –1; 3; 7.

Xem đáp án

Ta có:

u₁ = 2.

$u_{2} = 2 . u_{1} - 1 = 2 .2 - 1 = 3$ .

$u_{3} = 2 . u_{2} - 1 = 2 .3 - 1 = 5$ .

Vậy ba số hạng đầu tiên của dãy số lần lượt là: 2; 3; 5.

Chọn đáp án A.

Câu 3:

Cho dãy số (u_n), biết

u_{n} = \frac{n - 1}{n + 2}, \forall n \in ℕ^{*}

. Tìm khẳng định sai

A. u₁ = 0.

B. (u_n) bị chặn trên.

C. (u_n) là dãy số giảm.

D. $u_{5} = \frac{4}{7}$ .

Xem đáp án

* Ta có: $u_{1} = \frac{1 - 1}{1 + 2} = 0$ . Phương án A đúng.

* Ta có $u_{n} = \frac{n - 1}{n + 2} = \frac{(n + 2) - 3}{n + 2} = 1 - \frac{3}{n + 2} < 1$ .

Suy ra: nên bị chặn trên. Phương án B đúng.

* Ta có:

$u_{n + 1} - u_{n} = \frac{n}{n + 3} - \frac{n - 1}{n + 2} = \frac{n^{2} + 2 n - n^{2} + n - 3 n + 3}{(n + 3) (n + 2)} = \frac{3}{(n + 3) (n + 2)} > 0; \forall n \in ℕ *$

Suy ra (u_n) là dãy số tăng. Phương án C sai.

* Ta có: $u_{5} = \frac{5 - 1}{5 + 2} = \frac{4}{7}$ . Phương án D đúng.

Vậy khẳng định sai là: “ (u_n) là dãy số giảm”.

Câu 4:

Cho dãy số (u_n), biết

u_{n} = 2^{\frac{1}{n^{2} + 3 n + 2}}, \forall n \in ℕ^{*}

. Tích của 2021 số hạng đầu tiên bằng

A. $2^{\frac{505}{1011}} .$

B. $2^{\frac{1010}{2023}} .$

C. $2^{\frac{2021}{4046}} .$

D. $2^{\frac{2022}{4047}} .$

Xem đáp án

Ta có:

$\frac{1}{n^{2} + 3 n + 2} = \frac{1}{(n + 1) (n + 2)} = \frac{1}{1 .2 - 1 .1} (\frac{1}{n + 1} - \frac{1}{n + 2}) = \frac{1}{n + 1} - \frac{1}{n + 2}$

Suy ra: $u_{n} = 2^{\frac{1}{n + 1} - \frac{1}{n + 2}}$ .

$\Rightarrow$ $\{\begin{cases} u_{1} = 2^{\frac{1}{2} - \frac{1}{3}} \\ u_{2} = 2^{\frac{1}{3} - \frac{1}{4}} \\ u_{3} = 2^{\frac{1}{4} - \frac{1}{5}} \\ . .... \\ u_{2021} = 2^{\frac{1}{2022} - \frac{1}{2023}} \end{cases}$ .

$\Rightarrow u_{1} . u_{2} . u_{3} . ... u_{2021} = 2^{\frac{1}{2} - \frac{1}{3}} . 2^{\frac{1}{3} - \frac{1}{4}} . 2^{\frac{1}{4} - \frac{1}{5}} . {...2}^{\frac{1}{2022} - \frac{1}{2023}} = 2^{\frac{1}{2} - \frac{1}{3} + \frac{1}{3} - \frac{1}{4} + \frac{1}{4} - \frac{1}{5} + . ... + \frac{1}{2022} - \frac{1}{2023}} = 2^{\frac{1}{2} - \frac{1}{2023}} = 2^{\frac{2021}{4046}}$

Chọn đáp án C.

Câu 5:

Cho dãy số (u_n), biết

\{\begin{cases} u_{1} = 1 \\ u_{n + 1} = u_{n} . 3^{n} \end{cases}

,

\forall n \in ℕ^{*}

. Số hạng thứ 10 của dãy số là:

A. $3^{45}$ .

B. $3^{36}$ .

C. $3^{9!}$ .

D. $3^{10!}$ .

Xem đáp án

Ta có: $\{\begin{cases} u_{1} = 1 \\ u_{2} = u_{1} . 3^{1} \\ u_{3} = u_{2} . 3^{2} \\ . .... \\ u_{10} = u_{9} . 3^{9} \end{cases}$

$\Rightarrow u_{1} . u_{2} . u_{3} . ... u_{10}$ $= u_{1} . u_{2} . ... u_{9} . 3^{1} . 3^{2} . {...3}^{9}$ $\Leftrightarrow u_{10} = 3^{1 + 2 + . ... + 9} = 3^{\frac{9 .10}{2}} = 3^{45}$ .

Chọn đáp án A.

Câu 6:

Một cấp số cộng (u_n) có u₁ = 2, u₂₁ = 62. Công sai của cấp số cộng đó là

A. 2.

B. 1.

C. 4.

D. 3.

Xem đáp án

Áp dụng công thức số hạng tổng quát của cấp số cộng $u_{n} = u_{1} + (n - 1) d$

Ta có: $u_{21} = u_{1} + (21 - 1) d$ $\Leftrightarrow 62 = 2 + 20 d$ $\Leftrightarrow d = 3$ .

Vậy công sai của cấp số cộng đó là 3.

Chọn đáp án D.

Câu 7:

Tìm m để số: 4; 5m + 1; 32 – 7m theo thứ tự lập thành cấp số cộng.

A. m = – 2.

B. m = 2.

C. m = 11.

D. m = 1.

Xem đáp án

Áp dụng tính chất của cấp số cộng $u_{k} = \frac{u_{k - 1} + u_{k + 1}}{2}$ với $k \geq 2$ ta có:

Ba số: 4 ; 5m+1; 32-7m theo thứ tự lập thành cấp số cộng

$\Leftrightarrow 5 m + 1 = \frac{4 + (32 - 7 m)}{2}$ $\Leftrightarrow 10 m + 2 = - 7 m + 36$ $\Leftrightarrow m = 2$ .

Vậy m = 2 thỏa mãn đề bài.

Chọn đáp án B.

Câu 8:

Một cấp số cộng (u_n) có 8 số hạng, biết u₁ = – 2, u₈ = 32. Tổng các số hạng của cấp số cộng đó là

A. 136.

B. 30.

C. 120.

D. 240.

Xem đáp án

Ta có tổng của 8 số hạng của cấp số cộng $S_{8} = \frac{(u_{1} + u_{8}) . 8}{2} = 4 (- 2 + 32) = 120$

Chọn đáp án C.

Câu 9:

Cho cấp số cộng (u_n) có u₁ = 1, công sai d = 3. Tìm số hạng tổng quát của cấp số cộng.

A.

u_{n} = - 3 n + 4

.

B. $u_{n} = 3 n - 3$

C. $u_{n} = 3 n - 2$

D. $u_{n} = 3 n + 1$

Xem đáp án

Áp dụng công thức số hạng tổng quát $u_{n} = u_{1} + (n - 1) d$ ta có: $u_{n} = 1 + (n - 1) . 3 \Leftrightarrow u_{n} = 3 n - 2$ .

Chọn đáp án C.

Câu 10:

Cho cấp số cộng (u_n) thỏa mãn

\{\begin{cases} u_{2} + u_{5} - u_{3} = 10 \\ u_{1} + u_{6} = 17 \end{cases}

Tính $S = u_{2} + u_{5} + u_{8} + . .. + u_{2021}$ .

A. 2 043 231.

B. 2 043 230.

C. 2043 905.

D. 2 042 220.

Xem đáp án

Cấp số cộng (u_n) có công sai là d.

Ta có hệ phương trình: $\{\begin{cases} u_{2} + u_{5} - u_{3} = 10 \\ u_{1} + u_{6} = 17 \end{cases} \Leftrightarrow \{\begin{cases} u_{1} + 3 d = 10 \\ 2 u_{1} + 5 d = 17 \end{cases}$ $\Leftrightarrow \{\begin{cases} u_{1} = 1 \\ d = 3 \end{cases}$

$u_{2}, u_{5}, u_{8}, ..., u_{2021}$ là một cấp số cộng $(v_{n})$ có: $v_{1} = u_{2} = 4$ , công sai $d^{'} = 9$ , $n = 674$ .

$S = u_{2} + u_{5} + u_{8} + . .. + u_{2021} = \frac{v_{1} + v_{674}}{2} . 674 = 337 . (2 v_{1} + 673 d^{'}) = 2 043 905$

Chọn đáp án C.

Câu 11:

Cho cấp số cộng (u_n), biết u₂ = 4 và u₄ = 6. Giá trị của u₉ bằng

A. 11.

B. 10.

C. 9.

D. 8.

Xem đáp án

Cấp số cộng (u_n) có công sai là d.

Ta có hệ phương trình: $\{\begin{cases} u_{1} + d = 4 \\ u_{1} + 3 d = 6 \end{cases}$ $\Rightarrow \{\begin{cases} u_{1} = 3 \\ d = 1 \end{cases}$

Vậy $u_{9} = u_{1} + 8 d = 11$ .

Chọn đáp án A.

Câu 12:

Cho cấp số nhân (u_n) có số hạng thứ ba u₃ = 7 và số hạng thứ năm u₅ = 28. Biết công bội là một số dương khi đó công bội của cấp số nhân (u_n) là

A. 4.

B.

\frac{7}{2}

.

C. 2.

D. 21.

Xem đáp án

Cấp số nhân (u_n) có công bội là q.

Ta có hệ phương trình: $\{\begin{cases} u_{3} = 7 \\ u_{5} = 28 \end{cases} \Leftrightarrow \{\begin{cases} u_{1} . q^{2} = 7 \\ u_{1} . q^{4} = 28 \end{cases} \Rightarrow q^{2} = 4$ .

Mà q > 0 nên q = 2.

Chọn đáp án C.

Câu 13:

Cho cấp số nhân (u_n) có số hạng thứ nhất u₁ = 16, công bội

q = \frac{1}{2}

. Số hạng thứ mười u₁₀ là

A. 32.

B.

\frac{1}{16}

.

C. 120.

D.

\frac{1}{32}

.

Xem đáp án

Ta có số hạng thứ mười $u_{10} = u_{1} . q^{9} = 16 . {(\frac{1}{2})}^{9} = \frac{1}{32}$

Chọn đáp án D.

Câu 14:

Cho cấp số nhân (u_n) có số hạng đầu u₁ = – 2, công bội q = 3. Số –39366 là số hạng thứ mấy của cấp số nhân đã cho?

A. 10.

B. 9.

C. 8.

D. 11.

Xem đáp án

Gọi u_n là số hạng thứ n của dãy.

Ta có: số hạng tổng quát của cấp số nhân: $u_{n} = u_{1} . q^{n - 1}$

$\Rightarrow - 39366 = - 2 {.3}^{n - 1}$ $\Leftrightarrow 3^{n - 1} = 19683$ $\Leftrightarrow 3^{n - 1} = 3^{9}$ $\Leftrightarrow n = 10$ .

Vậy –39366 là số hạng thứ 10.

Chọn đáp án A.

Câu 15:

Cho cấp số nhân (u_n) biết số hạng đầu u₁ = 2, công bội q = –2. Tổng 10 số hạng đầu của cấp số nhân là

A. 2046.

B. –2046.

C. 682.

D. –682.

Xem đáp án

Tổng 10 số hạng đầu của cấp số nhân: $S_{10} = u_{1} \frac{q^{10} - 1}{q - 1} = 2 . \frac{{(- 2)}^{10} - 1}{- 2 - 1} = - 682$

Chọn đáp án D.

Câu 16:

Cho cấp số nhân (u_n) có S₅ = 30, S₁₀ = 50. Tìm công bội q của cấp số nhân.

A. q = 2.

B. $q = \sqrt{2}$ .

C. $q = \sqrt[5]{\frac{3}{2}}$ .

D. $q = \sqrt[5]{\frac{2}{3}}$ .

Xem đáp án

+) Trường hợp q = 1.

Ta có $u_{1} = u_{2} = . .. = u_{n} = . ..$

Khi đó từ giả thiết ta có: $\{\begin{cases} u_{1} + u_{2} + . .. + u_{5} = 30 \\ u_{1} + u_{2} + . .. + u_{10} = 50 \end{cases}$ $\Leftrightarrow \{\begin{cases} 5 u_{1} = 30 \\ 10 u_{1} = 50 \end{cases}$ $\Leftrightarrow \{\begin{cases} u_{1} = \frac{30}{5} \\ u_{1} = 5 \end{cases}$ (vô lý)

+) Trường hợp $q \neq 1$ .

Theo giả thiết ta có $\{\begin{cases} S_{5} = 30 \\ S_{10} = 50 \end{cases} \Leftrightarrow \{\begin{cases} \frac{u_{1} (1 - q^{5})}{1 - q} = 30 (1) \\ \frac{u_{1} (1 - q^{10})}{1 - q} = 50 (2) \end{cases}$

Chia vế cho vế của (2) cho (1) ta được: $1 + q^{5} = \frac{5}{3} \Leftrightarrow q^{5} = \frac{2}{3} \Leftrightarrow q = \sqrt[5]{\frac{2}{3}}$ .

Chọn đáp án D.

Câu 17:

Tập nghiệm của phương trình

1 + x + {(1 + x)}^{2} + {(1 + x)}^{3} + . .. + {(1 + x)}^{10}

= 0

là

A. $S = \{1; 2\}$

B. $S = \{- 1; - 2\}$

C. $S = \{0; - 1; - 2\}$

D. $S = \{0; 1; 2\}$

Xem đáp án

Nhận xét: x = 0 không phải là nghiệm của phương trình đã cho.

Ta có vế trái của phương trình đã cho là tổng của 10 số hạng đầu của một cấp số nhân có số hạng đầu $u_{1} = 1 + x$ và công bội $q = 1 + x$ .

Phương trình đã cho trở thành

$(x + 1) . \frac{[1 - {(x + 1)}^{10}]}{1 - (1 + x)} = 0$ $\Leftrightarrow \{\begin{cases} x \neq 0 \\ [\begin{array}{l} x + 1 = 0 \\ 1 - {(1 + x)}^{10} = 0 \end{array} \end{cases}$ $\Leftrightarrow \{\begin{cases} x \neq 0 \\ [\begin{array}{l} x = - 1 \\ {(1 + x)}^{10} = 1 \end{array} \end{cases}$

$\Leftrightarrow \{\begin{cases} x \neq 0 \\ [\begin{array}{l} x = - 1 \\ 1 + x = 1 \\ 1 + x = - 1 \end{array} \end{cases}$ $\Leftrightarrow \{\begin{cases} x \neq 0 \\ [\begin{array}{l} x = - 1 (thỏa mã n) \\ x = 0 (loại) \\ x = - 2 (thỏa mã n) \end{array} \end{cases}$

Vậy tập nghiệm của phương trình đã cho là $S = \{- 1; - 2\}$ .

Chọn đáp án B.

Câu 18:

Giá trị của

\lim \frac{n - 2021 \sqrt{n}}{2 n + 2021}

bằng

A. $+ \infty$

B. $- \infty$

C. $\frac{1}{2}$

D. 1

Xem đáp án

$\lim \frac{n - 2021 \sqrt{n}}{2 n + 2021} = \lim \frac{1 - 2021 . \sqrt{\frac{1}{n}}}{2 + \frac{2021}{n}} = \frac{1}{2}$

Chọn đáp án C.

Câu 19:

Dãy số nào sau đây có giới hạn bằng 0?

A. ${(\frac{2021}{643 π})}^{n}$

B. ${(\frac{2 π}{7})}^{n}$

C. ${(\frac{π}{3})}^{n}$

D. ${(\frac{4}{π})}^{n}$

Xem đáp án

Ta có $\lim q^{n} = 0$ nếu $|q| < 1$ .

Mà $|\frac{2021}{643 π}| > 1$ , $|\frac{π}{3}| > 1$ , $|\frac{4}{π}| > 1$ , $|\frac{2 π}{7}| < 1$ .

Do đó $\lim {(\frac{2 π}{7})}^{n} = 0$ .

Chọn đáp án B.

Câu 20:

Tính

I = \lim (nsin \frac{1}{2 n})

.

A. $+ \infty$ .

B. 2.

C. $\frac{1}{2}$ .

D. 1.

Xem đáp án

Ta có $\frac{1}{2 n} \to 0$ khi $n \to + \infty$ .

Áp dụng kết quả $\lim_{x \to 0} \frac{sinx}{x} = 1$ , ta có $I = \lim (nsin \frac{1}{2 n}) = \lim (\frac{1}{2} . \frac{\sin \frac{1}{2 n}}{\frac{1}{2 n}})$ $= \frac{1}{2} . 1 = \frac{1}{2}$

Vậy $I = \frac{1}{2}$

Chọn đáp án C.

Câu 21:

Tính $I = \lim \frac{n^{2} (3 n + 2)}{{(n + 1)}^{2} (n + 3)}$

A. 1.

B. 3.

C. $\frac{2}{3}$ .

D. 2.

Xem đáp án

Ta có $I = \lim \frac{n^{2} (3 n + 2)}{{(n + 1)}^{2} (n + 3)}$ $= \lim \frac{3 + \frac{2}{n}}{{(1 + \frac{1}{n})}^{2} (1 + \frac{3}{n})}$ $= 3$

Chọn đáp án B.

Câu 22:

Giá trị của

\lim \frac{2^{2019} n^{3} + n^{2} - 1}{2^{2018} n^{2} + n - 2 n^{3}}

bằng

A. $- 2^{2018}$

B. $2^{2018}$

C. 2

D. 0

Xem đáp án

$\lim \frac{2^{2019} n^{3} + n^{2} - 1}{2^{2018} n^{2} + n - 2 n^{3}}$ $= \lim \frac{2^{2019} + \frac{1}{n} - \frac{1}{n^{3}}}{\frac{2^{2018}}{n} + \frac{1}{n^{2}} - 2}$ $= \frac{2^{2019}}{- 2}$ $= - 2^{2018}$

Chọn đáp án A.

Câu 23:

Giá trị của $\lim \sqrt{n} (\sqrt{2^{2020} n + 2021}$ $- \sqrt{2^{2020} n - 2021})$ là

A. $\frac{2021}{2^{1010}}$

B. $\frac{2021}{2^{2020}}$

C. $+ \infty$

D. $- \infty$

Xem đáp án

$\lim \sqrt{n} (\sqrt{2^{2020} n + 2021} - \sqrt{2^{2020} n - 2021}) = \lim \frac{4042 \sqrt{n}}{\sqrt{2^{2020} n + 2021} + \sqrt{2^{2020} n - 2021}}$

$= \lim \frac{4042}{\sqrt{2^{2020} + \frac{2021}{n}} + \sqrt{2^{2020} - \frac{2021}{n}}} = \frac{4042}{2^{1010} + 2^{1010}} = \frac{2 .2021}{2 {.2}^{1010}} = \frac{2021}{2^{1010}}$

Chọn đáp án A.

Câu 24:

Biết

\lim (\sqrt{n^{2} - \frac{1}{11} n + 3} - n) = a

, với

a \in ℚ

. Tính

P = a^{2} + 1

.

A. $\frac{485}{484}$

B. $\frac{483}{484}$

C. $\frac{1}{121}$

D. $\frac{1}{484}$

Xem đáp án

$\lim (\sqrt{n^{2} - \frac{1}{11} n + 3} - n)$ $= \lim \frac{- \frac{1}{11} n + 3}{\sqrt{n^{2} - \frac{1}{11} n + 3} + n}$ $= \lim \frac{- \frac{1}{11} + \frac{3}{n}}{\sqrt{1 - \frac{1}{11 n} + \frac{3}{n^{2}}} + 1}$ $= \frac{- \frac{1}{11}}{1 + 1} = - \frac{1}{22}$

$P = a^{2} + 1 = {(- \frac{1}{22})}^{2} + 1 = \frac{485}{484}$

Chọn đáp án A.

Câu 25:

Biết

\lim (\frac{1}{6} + \frac{1}{12} + \frac{1}{24} + . .. + \frac{1}{3 {.2}^{n}}) = \frac{a}{b}

, với

a, b \in ℕ

và

\frac{a}{b}

tối giản. Tính

P = a - b^{2}

A. 8.

B. –8.

C. –2.

D. 10.

Xem đáp án

Ta có

$\frac{1}{6} + \frac{1}{12} + \frac{1}{24} + . .. + \frac{1}{3 {.2}^{n}} = \frac{1}{3 .2} + \frac{1}{3 {.2}^{2}} + \frac{1}{3 {.2}^{3}} + . .. + \frac{1}{3 {.2}^{n}} = \frac{1}{3} (\frac{1}{2} + \frac{1}{2^{2}} + \frac{1}{2^{3}} + . .. + \frac{1}{2^{n}}) = \frac{1}{3} . \frac{1}{2} . \frac{\frac{1}{2^{n}} - 1}{\frac{1}{2} - 1} = \frac{1}{3} - \frac{1}{3} . \frac{1}{2^{n}}$

Khi đó $\lim (\frac{1}{6} + \frac{1}{12} + \frac{1}{24} + . .. + \frac{1}{3 {.2}^{n}})$ $= \lim (\frac{1}{3} - \frac{1}{3} . \frac{1}{2^{n}})$ $= \frac{1}{3}$ .

Ta có a = 1, b = 3. Vậy $P = a - b^{2} = - 8$ .

Chọn đáp án B.

Câu 26:

Cho hình hộp ABCD.A'B'C'D'. Đường thẳng BD không song song với mặt phẳng nào dưới đây

A.

(A^{'} B^{'} C^{'} D^{'})

B. $({AB}^{'} D^{'})$ .

C. $({CB}^{'} D^{'})$ .

D. $({BA}^{'} C^{'})$ .

Xem đáp án

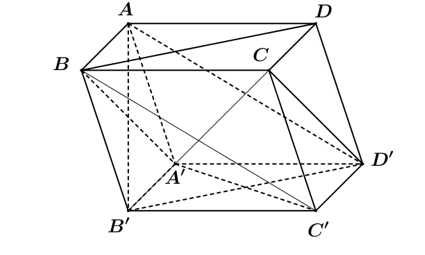
Cho hình hộp ABCD.A'B'C'D'. Đường thẳng BD không song song với mặt phẳng nào dưới đây (ảnh 1)

Đường thẳng BD và mặt phẳng (BA'C') có chung điểm B nên đường thẳng BD không song song với mặt phẳng (BA'C').

Chọn đáp án D.

Câu 27:

Cho tứ diện ABCD. Gọi M, N, P lần lượt nằm trên các cạnh AB, AC, AD sao cho AM = 2MB, AN = 2NC, AP = PD. Mệnh đề nào sau đây là mệnh đề đúng?

A. ND // (ABC).

B. MP // (BCD).

C. NP // (BCD).

D. MN // (BCD).

Xem đáp án

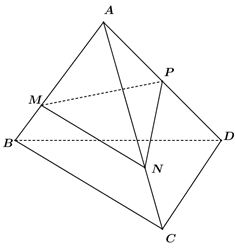
Cho tứ diện ABCD. Gọi M, N, P lần lượt nằm trên các cạnh AB, AC, AD sao cho AM = 2MB, AN = 2NC, AP = PD. Mệnh đề nào sau đây là mệnh đề đúng? (ảnh 1)

Ta nhận thấy N nằm trên mặt phẳng (ABC) nên đường thẳng ND không song song với mặt phẳng (ABC). Vậy đáp án A sai.

Từ giả thiết $\frac{A M}{M B} \neq \frac{A P}{P D}$ suy ra nên MP cắt BD, do đó đường thẳng MP không song song với mặt phẳng (BCD).

Tương tự ta lại có NP cắt CD nên đường thẳng NP không song song với mặt phẳng (BCD).

Mặt khác MN // BC và MN không nằm trên mặt phẳng (BCD) nên MN // (BCD).

Chọn đáp án D.

Câu 28:

Cho hai mặt phẳng (P) và (Q) song song với nhau. Đường thẳng d nằm trong mặt phẳng (P). Khẳng định nào là khẳng định đúng?

A. d có thể cắt (Q) hoặc nằm trong (Q).

B. d nằm trong (Q).

C. d cắt (Q).

D. d song song với (Q).

Xem đáp án

$\{\begin{cases} (P) // (Q) \\ d \subset (P) \end{cases} \Rightarrow$ d và (Q) không có điểm chung hay d song song với (Q).

Chọn đáp án D.

Câu 29:

Cho hình chóp S.ABCD có đáy ABCD là một hình bình hành. Gọi A', B', C' lần lượt là trung điểm của các cạnh SA, SB, SC. Khẳng định nào sau đây là khẳng định đúng?

A.

A^{'} B^{'} // (SAB)

.

B. $(A^{'} B^{'} C^{'}) // (ACD)$ .

C. $A^{'} B^{'} // (SBC)$ .

D. $({BA}^{'} C^{'}) // (B^{'} AC)$ .

Xem đáp án

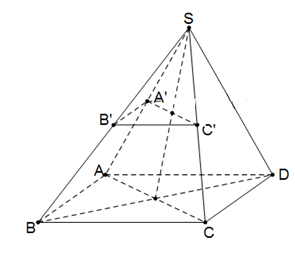
aCho hình chóp S.ABCD có đáy ABCD là một hình bình hành. Gọi A', B', C' lần lượt là trung điểm của các cạnh SA, SB, SC. Khẳng định nào sau đây là khẳng định đúng? (ảnh 1)

Ta có: $\{\begin{cases} B^{'} C^{'} // AD \\ B^{'} C^{'} ⊄ (ACD) \end{cases} \Rightarrow B^{'} C^{'} // (ACD) (1)$

$\{\begin{cases} A^{'} B^{'} // CD \\ A^{'} B^{'} ⊄ (ACD) \end{cases} \Rightarrow A^{'} B^{'} // (ACD) (2)$

Từ (1), (2) $\Rightarrow (A^{'} B^{'} C^{'}) // (ACD) .$

+ Đáp án A sai vì $A^{'} B^{'} \subset (SAB)$ .

+ Đáp án C sai vì $A^{'} B^{'} \cap SB = \{B^{'}\}$ .

+ Đáp án D sai vì $B^{'} C \cap {BC}^{'}$ .

Chọn đáp án B.

Câu 30:

Cho hình hộp ABCD.A'B'C'D'. Mệnh đề nào sai trong các mệnh đề sau?

A. $\vec{{AB}^{'}} = \vec{AB} + \vec{{AA}^{'}} + \vec{{AD}^{'}}$

B. $\vec{{AC}^{'}} = \vec{AB} + \vec{AD} + \vec{{AA}^{'}}$

C. $\vec{{AB}^{'}} = \vec{{DC}^{'}}$

D. $\vec{{DB}^{'}} = \vec{{DC}^{'}} + \vec{DA}$

Xem đáp án

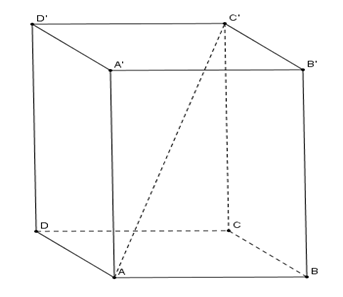
Cho hình hộp ABCD.A'B'C'D'. Mệnh đề nào sai trong các mệnh đề sau? (ảnh 1)

+) Theo quy tắc hình bình hành ta có $\vec{{AB}^{'}} = \vec{AB} + \vec{{AA}^{'}}$ nên đáp án A sai.

+) Theo quy tắc hình hộp ta có $\vec{{AC}^{'}} = \vec{AB} + \vec{AD} + \vec{{AA}^{'}}$ nên đáp án B đúng.

+) Theo quy tắc hình bình hành ta có $\vec{{AB}^{'}} = \vec{{DC}^{'}}$ nên đáp án C đúng.

+) Theo quy tắc hình bình hành ta có $\vec{{DB}^{'}} = \vec{{DC}^{'}} + \vec{DA}$ nên đáp án D đúng.

Câu 31:

Cho tứ diện ABCD có G là trọng tâm tứ diện. Khi hệ thức véc tơ

\vec{MG} = k . (\vec{MA} + \vec{MB} + \vec{MC} + \vec{MD})

đúng với mọi điểm M thì giá trị của k là

A. $k = \frac{1}{2}$

B. k = 1

C. $k = \frac{1}{3}$

D. $k = \frac{1}{4}$

Xem đáp án

G là trọng tâm tứ diện ABCD $\Leftrightarrow$ $\vec{GA} + \vec{GB} + \vec{GC} + \vec{GD} = \vec{0}$

$\Leftrightarrow$ $(\vec{GM} + \vec{MA}) + (\vec{GM} + \vec{MB})$ $+ (\vec{GM} + \vec{MC}) + (\vec{GM} + \vec{MD}) = \vec{0}$ , với mọi điểm M

$\Leftrightarrow$ $\vec{MG} = \frac{1}{4} . (\vec{MA} + \vec{MB} + \vec{MC} + \vec{MD})$ , với mọi điểm M.

Vậy $k = \frac{1}{4}$

Chọn đáp án D.

Câu 32:

Cho hình chóp S.ABCD, ABCD là hình bình hành, tam giác SAB là tam giác đều cạnh a. Tính tích vô hướng

\vec{DC} . \vec{BS}

?

A. $\frac{1}{2} a^{2}$

B. $\frac{\sqrt{3}}{2} a^{2}$

C. $\frac{\sqrt{2}}{2} a^{2}$

D. $- \frac{1}{2} a^{2}$

Xem đáp án

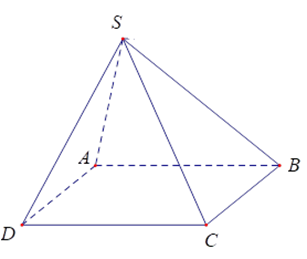
Cho hình chóp S.ABCD, ABCD là hình bình hành, tam giác SAB là tam giác đều cạnh a. Tính tích vô hướng DC→.BS→ ? (ảnh 1)

Tam giác SAB là tam giác đều cạnh a suy ra SA = AB = a và $\hat{SBA} = 60^{o}$ .

Do $\vec{DC} = \vec{AB}$ nên $(\vec{DC}; \vec{BS}) = (\vec{AB}; \vec{BS}) = 180^{o} -$ $(\vec{BA}; \vec{BS}) = 120^{0}$ .

Vậy $\vec{DC} . \vec{BS} = |\vec{DC}| . |\vec{BS}| . \cos (\vec{DC}; \vec{BS})$ $= a . a . \cos 120^{o} = - \frac{1}{2} a^{2}$

Chọn đáp án D.

Câu 33:

Trong không gian, khẳng định nào sau đây sai?

A. Hai đường thẳng phân biệt cùng vuông góc với một đường thẳng thì song song với nhau.

B. Hai đường thẳng vuông góc với nhau có thể cắt nhau hoặc chéo nhau.

C. Hai đường thẳng vuông góc với nhau thì góc giữa chúng bằng 90°.

D. Nếu a // b và $b ⊥ c$ thì $c ⊥ a$ .

Xem đáp án

Xét hình lập phương ABCD.A'B'C'D', ta có ${AA}^{'} ⊥ AB;$ ${AA}^{'} ⊥ AD$ nhưng AB và AD cắt nhau. Do đó phương án A sai.

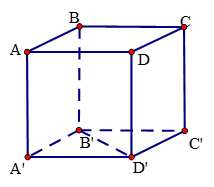
Trong không gian, khẳng định nào sau đây sai? (ảnh 1)

Chọn đáp án A.

Câu 34:

Cho hình chóp S.ABCD, có đáy ABCD là hình thoi góc $\hat{ABC}$ bằng 120°. Gọi M, N lần lượt là trung điểm của SA và SC. Số đo góc giữa hai đường thẳng MN và BC bằng

A. 30°.

B. 60°.

C. 45°.

D. 90°.

Xem đáp án

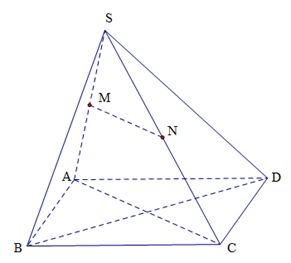
+ Vì M, N lần lượt là trung điểm của SA và SC suy ra MN song song AC.

+ $\hat{(MN, BC)} = \hat{(AC, BC)}$ .

+) Tứ giác ABCD là hình thoi có $\hat{ABC} = 120^{\circ}$ $\Rightarrow \hat{BCD} = 60^{\circ} \Rightarrow \hat{BCA} = 30^{\circ}$

Vậy $\hat{(MN, BC)} = \hat{(AC, BC)} = \hat{BCA} = 30^{\circ}$

Chọn đáp án A.

Câu 35:

Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh bằng 2a,

SA = a \sqrt{3}

. Gọi I là trung điểm của đoạn thẳng AC. Tính côsin góc giữa hai đường thẳng SA và BC biết SI vuông góc với cả hai đường thẳng AC và BI.

A. $\frac{17 \sqrt{3}}{40}$

B. $\frac{\sqrt{3}}{6}$

C. $\frac{\sqrt{3}}{3}$

D. $\frac{17 \sqrt{3}}{80}$

Xem đáp án

+ Vì tam giác ABC là tam giác đều suy ra IB vuông góc với AC.

+ Ta có: $\vec{SA} . \vec{BC} = (\vec{IA} - \vec{IS}) (\vec{IC} - \vec{IB})$ $= \vec{IA} . \vec{IC} - \vec{IA} . \vec{IB} - \vec{IS} . \vec{IC} + \vec{IS} . \vec{IB}$ $= - a^{2}$

+

\cos \hat{(SA, BC)} = |\cos \hat{(\vec{SA}, \vec{BC})}| = |\frac{\vec{SA} . \vec{BC}}{SA . BC}|

= |\frac{- a^{2}}{a \sqrt{3} . 2 a}| = \frac{\sqrt{3}}{6}

Chọn đáp án B.

Câu 36:

Cho dãy số (u_n) với $u_{n} = \frac{6 {.5}^{n} + 5 {.2}^{n}}{5^{n} + 2^{n}}$ . Khi đó tổng $S = \frac{1}{u_{1} - 5} + \frac{1}{u_{2} - 5} + . .. + \frac{1}{u_{2021} - 5}$ $= \frac{a}{3} - \frac{b}{3} {(\frac{2}{5})}^{c}$ trong đó a, b, c là các số nguyên dương.

Tính a + 2b² – 2c.

Xem đáp án

Ta có $u_{n} - 5 = \frac{6 {.5}^{n} + 5 {.2}^{n}}{5^{n} + 2^{n}} - 5 = \frac{5^{n}}{5^{n} + 2^{n}}$ $\Rightarrow \frac{1}{u_{n} - 5} = \frac{5^{n} + 2^{n}}{5^{n}} = 1 + {(\frac{2}{5})}^{n}$

$\Rightarrow S = \frac{1}{u_{1} - 5} + \frac{1}{u_{2} - 5} + . .. + \frac{1}{u_{2021} - 5} = [1 + {(\frac{2}{5})}^{1}] + [1 + {(\frac{2}{5})}^{2}] + . .. + [1 + {(\frac{2}{5})}^{2021}] = [2021 + \frac{2}{5} . \frac{1 - {(\frac{2}{5})}^{2021}}{1 - \frac{2}{5}}] = [2021 + \frac{2}{3} . (1 - {(\frac{2}{5})}^{2021})] = [\frac{6065}{3} - \frac{2}{3} {(\frac{2}{5})}^{2021}] .$

Mà $S = \frac{a}{3} - \frac{b}{3} {(\frac{2}{5})}^{c}$ nên $a = 6065;$ $b = 2;$ $c = 2021$ .

Nên $a + 2 b^{2} - 2 c = 6065 + 2 {.2}^{2} - 2 .2021$ $= 2031$

Câu 37:

Cho dãy số (u_n) thỏa mãn

\{\begin{cases} u_{1} = - 1 \\ u_{n} = 2021 u_{n - 1} - 1, \forall n \geq 2 \end{cases}

. Tìm giới hạn

\lim \frac{u_{n}}{2021^{n}}

Xem đáp án

+) Ta có: $u_{n} = 2021 u_{n - 1} - 1$ $\Leftrightarrow u_{n} - \frac{1}{2020} = 2021 (u_{n - 1} - \frac{1}{2020})$

+) Đặt $v_{n} = u_{n} - \frac{1}{2020}$ . Ta có $v_{1} = u_{1} - \frac{1}{2020} = - 1 - \frac{1}{2020} = - \frac{2021}{2020}$ và $v_{n} = 2021 v_{n - 1}, \forall n \geq 2$

Suy ra dãy (v_n) là cấp số nhân với công bội là q = 2021, $v_{1} = - \frac{2021}{2020}$

Khi đó $v_{n} = v_{1} . q^{n - 1} = - \frac{2021}{2020} . 2021^{n - 1}$ $= - \frac{2021^{n}}{2020}, \forall n \geq 1$

Do đó $u_{n} = v_{n} + \frac{1}{2020} = - \frac{2021^{n}}{2020} + \frac{1}{2020},$ $\forall n = 1,2,...$

+) Ta có: $\lim \frac{u_{n}}{2021^{n}} = \lim (- \frac{1}{2020} + \frac{1}{2020 {.2021}^{n}})$ $= - \frac{1}{2020}$

Vậy

\lim \frac{u_{n}}{2021^{n}} = - \frac{1}{2020}

Câu 38:

Cho hình lập phương ABCD.A'B'C'D'. M, N lần lượt thuộc các đoạn AD, A'C sao cho $AM = \frac{1}{5} AD, A^{'} N = \frac{2}{5} A^{'} C$ . Chứng minh:

a) (AB'D') // (BC'D).

b) ${AC}^{'} ⊥ A^{'} B .$

c) MN // (AB'D').

Xem đáp án

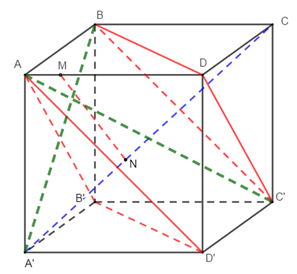
Cho hình lập phương ABCD.A'B'C'D'. M, N lần lượt thuộc các đoạn AD, A'C sao cho AM=15AD, A'N=25A'C . Chứng minh: a) (AB'D') // (BC'D). b) AC'⊥A'B. c) MN // (AB'D'). (ảnh 1)

a) Chứng minh $({AB}^{'} D^{'}) // ({BC}^{'} D)$ .

Từ giả thiết ta có $\begin{array}{l} BD // B^{'} D^{'} \\ {AB}^{'} // {DC}^{'} \end{array}\} \Rightarrow ({AB}^{'} D^{'}) // ({BC}^{'} D)$

b) Chứng minh ${AC}^{'} ⊥ A^{'} B$

Ta có: $\vec{{AC}^{'}} . \vec{A^{'} B} = (\vec{AB} + \vec{AD} + \vec{{AA}^{'}}) .$ $(\vec{AB} - \vec{{AA}^{'}})$

$= {\vec{AB}}^{2} + \vec{AD} . \vec{AB} + \vec{{AA}^{'}} . \vec{AB} - \vec{AB} . \vec{{AA}^{'}} - \vec{AD} . \vec{{AA}^{'}} - {\vec{{AA}^{'}}}^{2} \Rightarrow \vec{{AC}^{'}} ⊥ \vec{A^{'} B} \Rightarrow {AC}^{'} ⊥ A^{'} B$ .

c) Chứng minh $MN // ({AB}^{'} D^{'})$

Dễ thấy M, N không thuộc (AB'D').

$MN // ({AB}^{'} D^{'}) \Leftrightarrow \vec{MN}, \vec{{AB}^{'}}, \vec{{AD}^{'}}$ đồng phẳng $\Leftrightarrow \exists m, n : \vec{MN} = m \vec{{AB}^{'}} + n \vec{{AD}^{'}}$

Đặt $\vec{AB} = \vec{a}, \vec{AD} = \vec{b}, \vec{{AA}^{'}} = \vec{c}$

$\vec{MN} = \vec{AN} - \vec{AM} = \vec{{AA}^{'}} + \vec{A^{'} N} - \frac{1}{5} \vec{AD} = \vec{c} + \frac{2}{5} \vec{A^{'} C} - \frac{1}{5} \vec{b} = \vec{c} + \frac{2}{5} (\vec{a} + \vec{b} - \vec{c}) - \frac{1}{5} \vec{b} = \frac{2}{5} \vec{a} + \frac{1}{5} \vec{b} + \frac{3}{5} \vec{c}$

$\vec{{AB}^{'}} = \vec{a} + \vec{c}$ , $\vec{{AD}^{'}} = \vec{b} + \vec{c}$

$\vec{MN} = m \vec{{AB}^{'}} + n \vec{{AD}^{'}}$ $\Leftrightarrow \frac{2}{5} \vec{a} + \frac{1}{5} \vec{b} + \frac{3}{5} \vec{c}$ $= m \vec{a} + n \vec{b} + (m + n) \vec{c}$ $\Leftrightarrow \{\begin{cases} m = \frac{2}{5} \\ n = \frac{1}{5} \end{cases}$ $\Rightarrow \vec{MN} = \frac{2}{5} \vec{{AB}^{'}} + \frac{1}{5} \vec{{AD}^{'}}$

Vậy MN // (AB'D').

Đề kiểm tra Giữa kì 2 Toán 11 có đáp án (Mới nhất)

Đề kiểm tra Giữa kì 2 Toán 11 có đáp án (Mới nhất) (Đề 4)

Danh sách câu hỏi

Bài thi liên quan

Có thể bạn quan tâm

Các bài thi hot trong chương