39 câu hỏi trắc nghiệm thuộc Đề kiểm tra Giữa kì 2 Toán 11 có đáp án (Mới nhất) (Đề 18)

Câu 1:

Cho 2 dãy số $(a_{n}), (b_{n})$ với $a_{n} = \frac{{(- 1)}^{n}}{n}$ , $b_{n} = \frac{1}{n}$ . Khẳng định nào sau đây là đúng ?

A. $\lim \frac{a_{n}}{b_{n}} = + \infty$

B. Không tồn tại $\lim \frac{a_{n}}{b_{n}}$

C. $\lim \frac{a_{n}}{b_{n}} = 1$

D. $\lim \frac{a_{n}}{b_{n}} = 0$

Xem đáp án

Chọn B

Ta có: $\frac{a_{n}}{b_{n}} = {(- 1)}^{n}$ . Do đó không tồn tại $\lim \frac{a_{n}}{b_{n}}$ .

Câu 2:

Trong các giới hạn sau, giới hạn nào có giá trị khác với giới hạn còn lại?

A. $\lim \frac{3 n + 1}{- 3 n - 3}$

B. $\lim \frac{1 + n}{n - 1}$

C. $\lim \frac{1 - n}{n + 2}$

D. $\lim \frac{1 + 5 n}{6 - 5 n}$

Xem đáp án

Chọn B

Vì $\lim \frac{3 n + 1}{- 3 n - 3} = \lim \frac{1 - n}{n + 2} = \lim \frac{1 + 5 n}{6 - 5 n} = - 1$

Còn $\lim \frac{1 + n}{n - 1} = 1$

Câu 3:

Trong các mệnh đề sau, mệnh đề nào sai ?

A. Nếu $\lim u_{n} = a > 0$ ; $\lim v_{n} = 0$ và $v_{n} < 0, \forall n$ thì $\lim \frac{u_{n}}{v_{n}} = - \infty$ .

B.

\lim q^{n} = + \infty

( với

|q| > 1

).

C. $\lim n^{k} = + \infty$ với k là một số nguyên dương.

D. $\lim q^{n} = 0$ với

|q| < 1

.

Xem đáp án

Chọn B

Mệnh đề A đúng theo định lí về giới hạn vô cực.

Mệnh đề B chỉ đúng với q thỏa mãn q>1 còn với q<-1 thì không tồn tại giới hạn dãy số $q^{n}$ .

Mệnh đề C và D đúng theo kết quả của giới hạn đặc biệt.

Câu 4:

Khẳng định nào sau đây là đúng?

A. Dãy số $(u_{n})$ có giới hạn là số A (hay $u_{n}$ dần tới a) khi $n \to + \infty$ , nếu $\lim_{n \to + \infty} (u_{n} - a) = 0$ .

B. Dãy số

(u_{n})

có giới hạn là 0 khi n dần tới vô cực, nếu

|u_{n}|

có thể lớn hơn một số dương tùy ý, kể từ một số hạng nào đó trở đi.

C. Dãy số

(u_{n})

có giới hạn

+ \infty

khi

n \to + \infty

nếu

u_{n}

có thể nhỏ hơn một số dương bất kì, kể từ một số hạng nào đó trở đi.

D. Dãy số

(u_{n})

có giới hạn

- \infty

khi

n \to + \infty

nếu

u_{n}

có thể lớn hơn một số dương bất kì, kể từ một số hạng nào đó trở đi.

Xem đáp án

Chọn A

Theo định nghĩa giới hạn ta chọn đáp án đúng là A

Câu 5:

Mệnh đề nào sau đây là mệnh đề sai ?

A. $\lim \frac{1}{n} = 0$

B. $\lim q^{n} = 0$ nếu $|q| > 1$

C. $\lim n^{k} = + \infty$ với k nguyên dương

D. $\lim q^{n} = + \infty$ nếu q>1

Xem đáp án

Chọn B

$\lim q^{n} = 0$ nếu $|q| < 1$ .

Câu 6:

Cho 2 dãy số $(u_{n})$ và $(v_{n})$ thỏa mãn $\lim_{} u_{n} = 2$ , $\lim v_{n} = 5$ . Giá trị của $\lim \frac{u_{n}}{v_{n}}$ bằng:

A. $\frac{5}{2}$

B. $\frac{2}{5}$

C. 7

D. 3

Xem đáp án

Lời giải

Áp dụng định lí về giới hạn hữu hạn, ta có $\lim \frac{u_{n}}{v_{n}} = \frac{2}{5}$ .

Câu 7:

Cho

\lim (u_{n}) = 2, \lim (v_{n}) = - 3

. Khi đó giá trị của giới hạn

\lim (u_{n} . v_{n})

bằng?

A. 1

B. -6

C.5

D. -1

Xem đáp án

Lời giải.

Chọn B

Ta có: $\lim (u_{n} . v_{n}) = \lim (u_{n}) . \lim (v_{n}) = 2. (- 3) = - 6$

Câu 8:

Cho hai hàm số f(x) và g(x) có giới hạn hữu hạn khi x dần tới $x_{0}$ . Trong các mệnh đề sau mệnh đề nào đúng?

A. $\lim_{x \to x_{0}} [f (x) - g (x)] = \lim_{x \to x_{0}} g (x) - \lim_{x \to x_{0}} f (x)$

B. $\lim_{x \to x_{0}} [f (x) - g (x)] = \lim_{x \to x_{0}} f (x) + \lim_{x \to x_{0}} g (x)$

C. $\lim_{x \to x_{0}} [f (x) + g (x)] = \lim_{x \to x_{0}} f (x) + \lim_{x \to x_{0}} g (x)$

D. $\lim_{x \to x_{0}} [f (x) + g (x)] = \lim_{x \to x_{0}} f (x) - \lim_{x \to x_{0}} g (x)$

Xem đáp án

Lời giải

Theo định lý nếu f(x) và g(x) có giới hạn hữu hạn khi x dần tới $x_{0}$ thì $\lim_{x \to x_{0}} [f (x) + g (x)] = \lim_{x \to x_{0}} f (x) + \lim_{x \to x_{0}} g (x)$ .

Câu 9:

Giới hạn $\underset{x \to x_{0}}{l i m} f (x) = L$ khi và chỉ khi :

A. $\underset{x \to x_{0}^{+}}{l i m} f (x) = L$

B. $\underset{x \to x_{0}^{+}}{l i m} f (x) = \underset{x \to x_{0}^{-}}{l i m} f (x) = L$

C. $\underset{x \to x_{0}^{-}}{l i m} f (x) = L$

D. $\underset{x \to x_{0}^{+}}{l i m} f (x) \neq \underset{x \to x_{0}^{-}}{l i m} f (x) .$

Xem đáp án

Chọn B

$\underset{x \to x_{0}}{l i m} f (x) = L$ khi và chỉ khi $\underset{x \to x_{0}^{+}}{l i m} f (x) = \underset{x \to x_{0}^{-}}{l i m} f (x) = L$

Câu 10:

Cho $\lim_{x \to 1} f (x) = 2$ , $\lim_{x \to 1} g (x) = - 3$ . Tính $\lim_{x \to 1} [f (x) + g (x)]$ ?

A. 5

B. -5

C. -1

D. 1

Xem đáp án

Chọn C

Có $\lim_{x \to 1} [f (x) + g (x)]$ $\underset{x \to 1}{= \lim} f (x) + \lim_{x \to 1} g (x) = 2 + (- 3) = - 1$

Câu 11:

Giả sử ta có $\lim_{x \to + \infty} f (x) = a$ và $\lim_{x \to + \infty} g (x) = b$ . Trong các mệnh đề sau, mệnh đề nào sai?

A. $\lim_{x \to + \infty} [f (x) + g (x)] = a + b$

B. $\lim_{x \to + \infty} [f (x) . g (x)] = a . b$

C. $\lim_{x \to + \infty} \frac{f (x)}{g (x)} = \frac{a}{b}$

D. $\lim_{x \to + \infty} [f (x) - g (x)] = a - b$

Xem đáp án

Chọn đáp án C

Câu 12:

Với k là số nguyên dương , kết quả của giới hạn $\lim_{x \to - \infty} \frac{1}{x^{k}}$ là

A. 0

B. $+ \infty$

C. $- \infty$

D. 1

Xem đáp án

Chọn đáp án A

Câu 13:

Với k là số nguyên dương và k là số lẻ, kết quả của giới hạn

\lim_{x \to - \infty} x^{k}

là

A. $- \infty$

B. 0

C. $+ \infty$

D. 1

Xem đáp án

Chọn đáp án A

Câu 14:

Cho hàm số $f (x) = \{\begin{cases} x^{2} - 2 x + 1 khi x \neq 2 \\ m^{2} - 2 khi x = 2 \end{cases}$ . Giá trị của m để f(x) liên tục tại x=2 là:

A. $\sqrt{3}$

B. $- \sqrt{3}$

C. $\pm \sqrt{3}$

D. $\pm 3$

Xem đáp án

Lời giải

Chọn C

Hàm số liên tục tại x=2 $\Leftrightarrow \lim_{x \to 2} f (x) = f (2)$ .

Ta có $\lim_{x \to 2} (x^{2} - 2 x + 1) = 1$ .

Vậy $m^{2} - 2 = 1 \Leftrightarrow [\begin{array}{l} m = \sqrt{3} \\ m = - \sqrt{3} \end{array}$ .

Câu 15:

Trong các hàm sau, hàm nào không liên tục trên khoảng (-1,1) :

A. $f (x) = x^{4} - x^{2} + 2$

B. $f (x) = \sin x$

C. $f (x) = \frac{1}{x^{2} + 1}$

D. $f (x) = \sqrt{2 x - 1}$

Xem đáp án

Chọn đáp án D

Câu 16:

Trong các mệnh đề sau, mệnh đề nào sai? (Với giả thiết các đoạn thẳng và đường thẳng không song song hoặc trùng với phương chiếu).

A. Phép chiếu song song bảo toàn thứ tự ba điểm thẳng hàng.

B. Phép chiếu song song không làm thay đổi tỉ số độ dài của hai đoạn thẳng.

C. Hình chiếu của hai đường thẳng song song là hai đường thẳng song song hoặc trùng nhau.

D. Hình chiếu song song của đường thẳng là đường thẳng.

Xem đáp án

Chọn đáp án B

Câu 17:

Trong không gian cho 3 vectơ $\vec{u}, \vec{v}, \vec{w}$ không đồng phẳng. Mệnh đề nào sau đây là đúng?

A. Các vectơ $\vec{u} + \vec{v}, \vec{v}, \vec{w}$ đồng phẳng.

C. Các vectơ $\vec{u} + \vec{v}, \vec{v}, 2 \vec{w}$ không đồng phẳng.

D. Các vectơ $2 (\vec{u} + \vec{v}), - \vec{u} + - \vec{v}$ không đồng phẳng.

B. Các vectơ

\vec{u} + \vec{v}, - 2 \vec{u}, - 2 \vec{w}

không đồng phẳng.

C. Các vectơ

\vec{u} + \vec{v}, \vec{v}, 2 \vec{w}

không đồng phẳng.

D. Các vectơ

2 (\vec{u} + \vec{v}), - \vec{u}, - \vec{v}

không đồng phẳng.

Xem đáp án

Lời giải

Chọn C

Vì $\vec{u}, \vec{v}, \vec{w}$ không đồng phẳng nên :

 $\vec{u} + \vec{v}, \vec{v}, \vec{w}$ không đồng phẳng,

 $\vec{u} + \vec{v}, \vec{v}, 2 \vec{w}$ không đồng phẳng.

 $\vec{u} + \vec{v}, - 2 \vec{u}, 2 \vec{w}$ không đồng phẳng.

Các vectơ $2 (\vec{u} + \vec{v}), - \vec{u}, - \vec{v}$ hiển nhiên là đồng phẳng.

Câu 18:

Cho hình hộp $A B C D . A' B' C' D'$ , MN là các điểm thỏa $\vec{M A} = - \frac{1}{4} \vec{M D}$ , $\vec{N A'} = - \frac{2}{3} \vec{N C}$ . Mệnh đề nào sau đây đúng ?

A. $M N ∥ (A C' B)$

B. $M N ∥ (B C' D)$

C. $M N ∥ (A' C' D)$

D.

M N ∥ (B C' B)

Xem đáp án

Lời giải

Chọn B

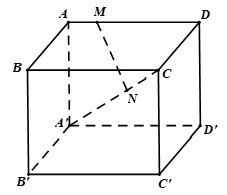
Cho hình hộp ABCDA'B'C'D',M,N là các điểm thỏa vectơ MA = -1/4vectơ MD (ảnh 1)

Đặt $\vec{B A} = \vec{a}, \vec{B B'} = \vec{b}, \vec{B C} = \vec{c}$ thì $\vec{a}, \vec{b}, \vec{c}$ là ba vec tơ không đồng phẳng và $\vec{B D} = \vec{B A} + \vec{A D} = \vec{B A} + \vec{B C} = \vec{a} + \vec{c}$

$\vec{B C'} = \vec{b} + \vec{c}, \vec{B A'} = \vec{a} + \vec{b}$ .

Ta có $\vec{M A} = - \frac{1}{4} \vec{M D} \Rightarrow \vec{B A} - \vec{B M} = - \frac{1}{4} (\vec{B D} - \vec{B M})$ $\Rightarrow \frac{5}{4} \vec{B M} = \vec{B A} + \frac{1}{4} \vec{B D}$

$\Rightarrow \vec{B M} = \frac{4 \vec{B A} + \vec{B D}}{5} = \frac{4 \vec{a} + (\vec{a} + \vec{c})}{5} = \frac{5 \vec{a} + \vec{c}}{5}$ .

Tương tự

$\vec{B N} = \frac{3 \vec{a} + 3 \vec{b} + 2 \vec{c}}{5}$ , $\vec{M N} = \vec{B N} - \vec{B M} = \frac{- 2 \vec{a} + 3 \vec{b} + \vec{c}}{5} = - \frac{2}{5} (\vec{a} + \vec{c}) + \frac{3}{5} (\vec{b} + \vec{c}) = - \frac{2}{5} \vec{B D} + \frac{3}{5} \vec{B C'}$

Suy ra $\vec{M N}, \vec{D B}, \vec{B C'}$ đồng phẳng mà $N \notin (B C' D) \Rightarrow M N ∥ (B C' D)$ .

Câu 19:

Cho tứ diện đều ABCD. Tích vô hướng $\vec{A B} . \vec{C D}$ bằng?

A. $a^{2}$

B. $\frac{a^{2}}{2}$

C. 0

D. $- \frac{a^{2}}{2}$

Xem đáp án

Chọn C

Cho tứ diện đều ABCD . Tích vô hướng vectơ AB. vectơ CD bằng? (ảnh 1)

$\vec{A B} . \vec{C D} =$ $(\vec{C B} - \vec{C A}) . \vec{C D}$ $= \vec{C B} . \vec{C D} - \vec{C A} . \vec{C D}$ $= C B . C D . \cos 60^{0} - C A . C D . \cos 60^{0}$

Câu 20:

Cho tứ diện ABCD có AB=AC=ADvà $\hat{B A C} = \hat{B A D} = 60^{0}$ . Hãy xác định góc giữa cặp vectơ $\vec{A B}$ và $\vec{C D}$ .

A. $60 °$

B. $45 °$

C. $120 °$

D. $90 °$

Xem đáp án

Cho tứ diện ABCD có AB=AC=ADvà góc BAC =góc BAD =60 độ . Hãy xác định góc giữa cặp vectơ AB và CD (ảnh 1)

Ta có: $\vec{A B} . \vec{C D} = \vec{A B} . (\vec{A D} - \vec{A C}) = \vec{A B} . \vec{A D} - \vec{A B} . \vec{A C}$

$= |\vec{A B}| . |\vec{A D}| \cos (\vec{A B}, \vec{A D}) - |\vec{A B}| . |\vec{A C}| \cos (\vec{A B}, \vec{A C})$

$= |\vec{A B}| . |\vec{A D}| \cos 60^{0} - |\vec{A B}| . |\vec{A C}| \cos 60^{0}$

Mà $A C = A D \Rightarrow \vec{A B} . \vec{C D} = 0 \Rightarrow (\vec{A B}, \vec{C D}) = 90^{0}$

Câu 21:

Tìm a để

\lim \frac{a . n^{2} + 4 n}{8 n^{2} + 3} = \frac{3}{4} .

A. a=6

B. a=3

C. a=27

D. a=9

Xem đáp án

Ta có $\lim \frac{a . n^{2} + 4 n}{8 n^{2} + 3} = \lim \frac{a + \frac{4}{n}}{8 + \frac{3}{n^{2}}} = \frac{\lim (a + \frac{4}{n})}{\lim (8 + \frac{3}{n^{2}})} = \frac{a}{8} .$

$\lim \frac{a . n^{2} + 4 n}{8 n^{2} + 3} = \frac{3}{4} \Leftrightarrow \frac{a}{8} = \frac{3}{4} \Leftrightarrow a = 6.$

Câu 22:

Tính tổng:

S = 1 - \frac{1}{2} + \frac{1}{4} - \frac{1}{8} + ... + \frac{1}{{(- 2)}^{n - 1}} + ...

A. S= $\frac{3}{2}$

B. S= $\frac{2}{3}$

C. S= 2

D. S= $\frac{1}{2}$

Xem đáp án

Lời giải

Chọn B

S là tổng của cấp số nhân lùi vô hạn với $u_{1} = 1; q = - \frac{1}{2}$ .

Do đó ta có: $S = \frac{u_{1}}{1 - q} = \frac{1}{1 - (- \frac{1}{2})} = \frac{2}{3}$ .

Câu 23:

Biết $\lim \frac{2 n^{3} + n^{2} - 4}{2 + n + 4 n^{3}} = L$ . Khi đó $1 - L^{2}$ bằng

A. 1

B. $\frac{3}{4}$

C. 0

D. $\frac{1}{5}$

Xem đáp án

Lời giải

Chọn B

Ta có $\lim \frac{2 n^{3} + n^{2} - 4}{2 + n + 4 n^{3}} = \lim \frac{n^{3} (2 + \frac{1}{n} - \frac{4}{n^{3}})}{n^{3} (\frac{2}{n^{3}} + \frac{1}{n^{2}} + 4)} = \frac{2}{4} = \frac{1}{2}$ .

Suy ra $L = \frac{1}{2}$ . Khi đó $1 - L^{2} = 1 - {(\frac{1}{2})}^{2} = \frac{3}{4}$ .

Câu 24:

Tính

\lim_{x \to - \infty} \frac{5 x - 3}{\sqrt{x^{2} - 5}}

A. $\frac{3}{5}$

B. $\frac{- 3}{5}$

C. 5

D. -5

Xem đáp án

Lời giải

Chọn D

Ta có:

$\lim_{x \to - \infty} \frac{5 x - 3}{\sqrt{x^{2} - 5}}$ $= \lim_{x \to - \infty} \frac{x (5 - \frac{3}{x})}{|x| \sqrt{1 - \frac{5}{x^{2}}}}$ $= \lim_{x \to - \infty} \frac{x (5 - \frac{3}{x})}{- x \sqrt{1 - \frac{5}{x^{2}}}}$ $= \lim_{x \to - \infty} \frac{5 - \frac{3}{x}}{- \sqrt{1 - \frac{5}{x^{2}}}} = - 5$ .

Câu 25:

Tính $\underset{x \to 0^{+}}{l i m} \frac{2 x + 1}{x}$ bằng

A. 2

B. $- \infty$

C. $+ \infty$

D. 1

Xem đáp án

Chọn C

Vì $\underset{x \to 0^{+}}{l i m} (2 x + 1) = 1$ , x>0 nên $\underset{x \to 0^{+}}{l i m} \frac{2 x + 1}{x} = + \infty$

Câu 26:

Cho

\lim_{x \to - \infty} (\sqrt{x^{2} + a x + 5} + x) = 5

. Giá trị của a bằng bao nhiêu ?

A. 6

B. 10

C. -10

D. -6

Xem đáp án

Lời giải

Chọn C

$\lim_{x \to - \infty} (\sqrt{x^{2} + a x + 5} + x) = \lim_{x \to - \infty} \frac{a . x + 5}{\sqrt{x^{2} + a x + 5} - x} = - \frac{a}{2}$

Mà $\lim_{x \to - \infty} (\sqrt{x^{2} + a x + 5} + x) = 5 \Rightarrow - \frac{a}{2} = 5 \Leftrightarrow a = - 10.$

Câu 27:

Cho hàm số $f (x) = \{\begin{cases} \frac{x^{2} - 4}{x + 2} khi x \neq - 2 \\ - 4 khi x = - 2 \end{cases}$ . Khẳng định nào sau đây là đúng?

A. Hàm số chỉ liên tục tại điểm x=-2 và gián đoạn tại các điểm $x \neq - 2$ .

B. Hàm số không liên tục trên R.

C. Hàm số liên tục trên R.

D. Hàm số không liên tục tại điểm x=-2.

Xem đáp án

Lời giải

Chọn C

+ Với $x \neq - 2$ : $f (x) = \frac{x^{2} - 4}{x + 2}$ .

Đây là hàm phân thức hữu tỉ nên hàm số liên tục trên $(- \infty; - 2), (- 2; + \infty)$ .

+ Tại x=-2: $f (- 2) = - 4$ ; $\lim_{x \to - 2} \frac{x^{2} - 4}{x + 2} = \lim_{x \to - 2} \frac{(x - 2) (x + 2)}{x + 2} = \lim_{x \to - 2} (x - 2) = - 4$ .

Hàm số đã cho liên tục tại x=-2

Vậy hàm số liên tục trên R.

Câu 28:

Cho hàm số: $f (x) = \{\begin{cases} \frac{x^{3} - 27}{x - 3}, x \neq 3 \\ 27 x = 3 \end{cases}$ , tìm khẳng định đúng trong các khẳng định sau:

I. f(x) liên tục tại x=3.

II. f(x) gián đoạn tại x=3.

III. f(x) liên tục trên R.

A. I và II

B. I và III

C. Chỉ I

D. II và III

Xem đáp án

Lời giải

Chọn B

Ta có:

$\lim_{x \to 3} f (x) = \lim_{x \to 3} \frac{x^{3} - 27}{x - 3} = \lim_{x \to 3} \frac{(x - 3) (x^{2} + 3 x + 9)}{x - 3} = \lim_{x \to 3} (x^{2} + 3 x + 9) = 27$ .

$f (3) = 27$ .

Ta lại thấy $\lim_{x \to 3} f (x) = f (3) = 27$ .

Vậy hàm số liên tục tại x=3 hay hàm số liên tục trên R.

Câu 29:

Cho hàm số $f (x) = \{\begin{cases} \frac{- x^{2} + x + 2}{x - 2} khi x \neq 2 \\ m x + 2 khi x = 2 \end{cases}$ . Với giá trị nào của m thì hàm số liên tục tại $x_{0} = 2$ .

A. $\frac{- 5}{2}$

B. $\frac{5}{2}$

C. 2

D. -2

Xem đáp án

Lời giải

Chọn A

TXĐ: D=R

$\lim_{x \to 2} f (x) = \lim_{x \to 2} \frac{- x^{2} + x + 2}{x - 2} = \lim_{x \to 2} \frac{(x - 2) (- x - 1)}{x - 2} = \lim_{x \to 2} (- x - 1) = - 3$ .

$f (2) = 2 m + 2$ .

Hàm số liên tục tại $x_{0} = 2$ khi và chỉ khi $\lim_{x \to 2} f (x) = f (2) \Leftrightarrow - 3 = 2 m + 2 \Leftrightarrow m = \frac{- 5}{2}$

Câu 30:

Tìm tham số m để hàm số $f (x) = \{\begin{cases} \frac{2 x^{2} - x - 6}{x - 2} nếu x \neq 2 \\ m x + 3 nếu x = 2 \end{cases}$ liên tục trên R.

A. m=-1

B. m= 1

C. m=2

D. m=4

Xem đáp án

Lời giải

Chọn C

Tập xác định D=R.

+ Nếu $x \neq 2$ thì hàm số $f (x) = \frac{2 x^{2} - x - 6}{x - 2}$ liên tục trên các khoảng $(- \infty; 2)$ và $(2; + \infty)$ .

+ Tại x=2: Ta có $f (2) = 2 m + 3$ .

$\lim_{x \to 2} f (x) = \lim_{x \to 2} \frac{2 x^{2} - x - 6}{x - 2} = \lim_{x \to 2} \frac{(2 x + 3) (x - 2)}{x - 2} = \lim_{x \to 2} (2 x + 3) = 7$ .

Hàm số f(x) liên tục trên R $\to$ f(x) liên tục tại điểm x=2 $\Leftrightarrow \lim_{x \to 2} f (x) = f (2)$

$\Leftrightarrow 2 m + 3 = 7 \Leftrightarrow m = 2$ .

Vậy m=2.

Câu 31:

Cho hình lập phương ABCDA'B'C'D'. Góc giữa hai đường thẳng BA' và CC' bằng:

A. $30 °$

B. $45 °$

C. $60 °$

D. $90 °$

Xem đáp án

Lời giải

Chọn B

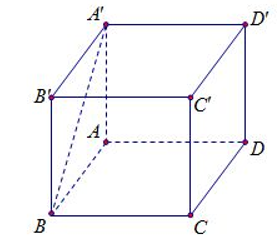
Ta có $C C' // B B' \Rightarrow (B A^{'}, C C') = (B A^{'}, B B') = \hat{A' B B'} = 45 °$ .

Câu 32:

Cho hình lập phương ABCDA'B'C'D' . Góc giữa hai vectơ

\vec{B^{'} D^{'}}

và

\vec{C D}

bằng

A. 90 $°$

B. $30 °$

C. $45 °$

D. $60 °$

Xem đáp án

Lời giải

Chọn C

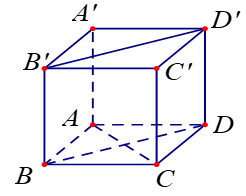
Ta có $\vec{C D} = \vec{B^{'} A^{'}}$ $\Rightarrow$ $(\vec{B^{'} D^{'}}, \vec{C D}) = (\vec{B^{'} D^{'}}, \vec{B^{'} A^{'}}) = \hat{A^{'} B^{'} D^{'}} = 45 °$ .

Câu 33:

Cho hình chóp S.ABC có

S A = S B = S C = A B = A C = 1

,

B C = \sqrt{2}

. Tính góc giữa hai đường thẳng AB và SC.

A. $60 °$

B. $120 °$

C. $30 °$

D. 45 $°$

Xem đáp án

Chọn A

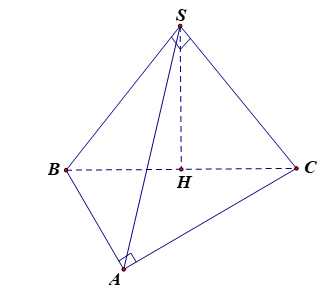
Cho hình chóp SABC có SA=SB=SC=Ab=AC=1 , BC=căn 2 . Tính góc giữa hai đường thẳng AB và SC. (ảnh 1)

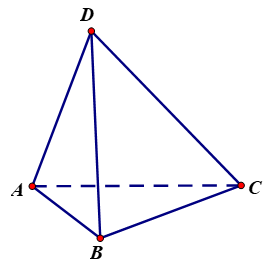
Tam giác ABC vuông tại A vì $A B = A C = 1$ , $B C = \sqrt{2}$ .

Tam giác SBC vuông tại B vì $S B = S C = 1$ , $B C = \sqrt{2}$ .

Ta có $\vec{S C} . \vec{A B} = \vec{S C} (\vec{S B} - \vec{S A})$ $= \vec{S C} . \vec{S B} - \vec{S C} . \vec{S A}$ $= 0 - S C . S B . \cos 60 ° = - \frac{1}{2}$ .

Suy ra $\cos (S C, A B) = |\cos (\vec{S C}, \vec{A B})|$ $= \frac{|\vec{S C} . \vec{A B}|}{S C . A B} = \frac{1}{2}$ .

Vậy góc giữa hai đường thẳng AB và SC bằng $60 °$ .

Câu 34:

Cho hình hộp ABCDEFGH Gọi I là tâm của hình bình hành ABEF và K là tâm của hình bình hành BCGF Khẳng định nào dưới đây là đúng?

A. $\vec{B D}, \vec{A K}, \vec{G F}$ đồng phẳng.

B. $\vec{B D}, \vec{I K}, \vec{G F}$ đồng phẳng.

C. $\vec{B D}, \vec{E K}, \vec{G F}$ đồng phẳng.

D. $\vec{B D}, \vec{I K}, \vec{G C}$ đồng phẳng

Xem đáp án

Chọn B

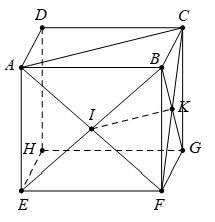
Cho hình hộp ABCDEFGH Gọi I là tâm của hình bình hành ABEF và K là tâm của hình bình hành BCGF Khẳng định nào dưới đây là đúng? (ảnh 1)

Vì I,K lần lượt là trung điểm của AF và CF

Suy ra IK là đường trung bình của tam giác AFC $\Rightarrow I K$ // $A C \Rightarrow I K$ $/ / (A B C D) .$

Mà (EF)//(ABCD) và $B D \subset (A B C D)$ suy ra ba vectơ $\vec{B D}, \vec{I K}, \vec{G F}$ đồng phẳng.

Câu 35:

Cho tứ diện ABCD. Gọi I , J lần lượt là trung điểm của các cạnh AB và CD , G là trung điểm của đoạn thẳng IJ. Trong các đẳng thức sau, đẳng thức nào đúng?

A. $\vec{G A} + \vec{G B} + \vec{G C} + \vec{G D} = \vec{0}$

B. $\vec{G A} + \vec{G B} + \vec{G C} + \vec{G D} = 2 \vec{I J}$

C. $\vec{G A} + \vec{G B} + \vec{G C} + \vec{G D} = \vec{J I}$

D. $\vec{G A} + \vec{G B} + \vec{G C} + \vec{G D} = 2 \vec{J I}$

Xem đáp án

Chọn A

Ta có G là trung điểm của đoạn thẳng IJ nên $\vec{G I} + \vec{G J} = \vec{0}$ .

Lại có I là trung điểm của cạnh AB nên $\vec{I A} + \vec{I B} = \vec{0}$

và J là trung điểm của cạnh CD nên $\vec{J C} + \vec{J D} = \vec{0}$ .

Từ đó ta có

$\vec{G A} + \vec{G B} + \vec{G C} + \vec{G D} = \vec{G I} + \vec{I A} + \vec{G I} + \vec{I B} + \vec{G J} + \vec{J C} + \vec{G J} + \vec{J D}$

$= 2 (\vec{G I} + \vec{G J}) + (\vec{I A} + \vec{I B}) + (\vec{J C} + \vec{J D}) = \vec{0}$ .

Câu 36:

Tìm giới hạn: $\lim \frac{2 n - \sqrt{4 n^{2} + n}}{n + \sqrt{n^{2} - 2 n}}$ .

Xem đáp án

Ta có:

Tìm giới hạn: lim 2n- căn 4n^2 +n/ n+ căn n^2 -2n . (ảnh 1)

\lim (n - \sqrt{n^{2} - 2 n})

= \lim \frac{(n - \sqrt{n^{2} - 2 n}) (n + \sqrt{n^{2} - 2 n})}{n + \sqrt{n^{2} - 2 n}} = \lim \frac{n^{2} - n^{2} + 2 n}{n + \sqrt{n^{2} - 2 n}} = \lim \frac{2 n}{n + \sqrt{n^{2} - 2 n}}

$= \lim \frac{2}{1 + \sqrt{1 - \frac{2}{n}}} = 1$

Suy ra $\lim \frac{2 n - \sqrt{4 n^{2} + n}}{n + \sqrt{n^{2} - 2 n}}$ $= - \frac{1}{4}$ .

Câu 37:

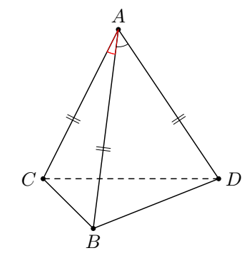
Cho tứ diện ABCD. Gọi G là trọng tâm tam giác BCD. Hai điểm M, N lần lượt thuộc BC, CD sao cho $\frac{B M}{B C} = \frac{1}{4}, \frac{N C}{N D} = \frac{3}{2}$ . Chứng minh rằng

bốn điểm A, M, N, G đồng phẳng.

Xem đáp án

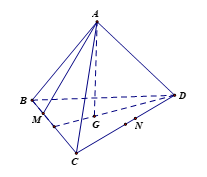
Cho tứ diện ABCD. Gọi G là trọng tâm tam giác BCD. Hai điểm M, N lần lượt thuộc BC, CD sao cho (ảnh 1)

Ta có: $\frac{B M}{B C} = \frac{1}{4} \Rightarrow \vec{M C} = - 3 \vec{M B} \Rightarrow 4 \vec{A M} = \vec{A C} + 3 \vec{A B}$ (1).

$\frac{N C}{N D} = \frac{3}{2} \Rightarrow 2 \vec{N C} = - 3 \vec{N D} \Rightarrow 5 \vec{A N} = 2 \vec{A C} + 3 \vec{A D}$ (2).

Cộng vế với vế của (1) với (2), ta được:

$\vec{A B} + \vec{A C} + \vec{A D} = \frac{4 \vec{A M} + 5 \vec{A N}}{3}$ (3)

Vì G trọng tâm $∆ A B C$ nên $\vec{A G} = \frac{1}{3} (\vec{A B} + \vec{A C} + \vec{A D})$ (4).

Thay (3) vào (4) được: $\vec{A G} = \frac{4}{9} \vec{A M} + \frac{5}{9} \vec{A N}$ , từ hệ thức này chứng tỏ ba véc tơ $\vec{A G}, \vec{A M}, \vec{A N}$ đồng phẳng. Suy ra bốn điểm A, M, N, G đồng phẳng.

Câu 38:

Tìm giới hạn của $B = \lim_{x \to + \infty} x (\sqrt{x^{2} + 2 x} - 2 \sqrt{x^{2} + x} + x)$ ?

Xem đáp án

Ta có: $\sqrt{x^{2} + 2 x} - 2 \sqrt{x^{2} + x} + x = \frac{2 x^{2} + 2 x + 2 x \sqrt{x^{2} + 2 x} - 4 x^{2} - 4 x}{\sqrt{x^{2} + 2 x} + 2 \sqrt{x^{2} + x} + x}$

$= 2 x \frac{\sqrt{x^{2} + 2 x} - x - 1}{\sqrt{x^{2} + 2 x} + 2 \sqrt{x^{2} + x} + x}$

$= \frac{- 2 x}{(\sqrt{x^{2} + 2 x} + 2 \sqrt{x^{2} + x} + x) (\sqrt{x^{2} + 2 x} + x + 1)}$ .

Nên $\begin{array}{l} B = \lim_{x \to + \infty} \frac{- 2 x^{2}}{(\sqrt{x^{2} + 2 x} + 2 \sqrt{x^{2} + x} + x) (\sqrt{x^{2} + 2 x} + x + 1)} \\ = \lim_{x \to + \infty} \frac{- 2}{(\sqrt{1 + \frac{2}{x}} + 2 \sqrt{1 + \frac{1}{x}} + 1) (\sqrt{1 + \frac{2}{x}} + 1 + \frac{1}{x})} = - \frac{1}{4} . \end{array}$