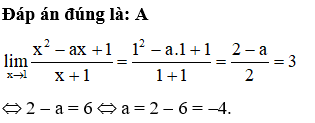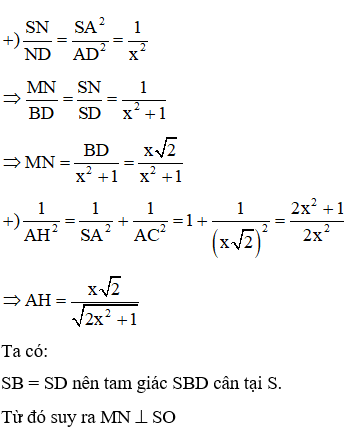Đề kiểm tra Giữa kì 2 Toán 11 có đáp án (Mới nhất)
Đề kiểm tra Giữa kì 2 Toán 11 có đáp án (Mới nhất) (Đề 10)
-
1528 lượt thi
-
50 câu hỏi
-
0 phút
Danh sách câu hỏi
Câu 3:
 Xem đáp án
Xem đáp án
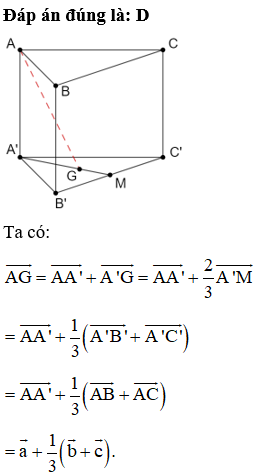
Đáp án đúng là: D
+) Nếu a // b và a ^ c thì b ^ c (Đúng)
+) Nếu a ^ b và a ^ c, đồng thời b, c cắt nhau và b, c nằm trong (a) thì a ^ (a) (Đúng)
+) Nếu a ^ (a) thì a vuông góc với mọi đường thẳng nằm trong (a) (Đúng)
+) Nếu a ^ (a) và b ^ (a) thì a // b (Sai vì a và b có thể trùng nhau).
Câu 10:
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Đặt f (x) = x3 + 3x + 1.
Khi x tiến đến -¥ thì x3 tiến đến -¥ và x tiến đến -¥.
Từ đó f (x) tiến đến -¥.
Vậy
Câu 13:
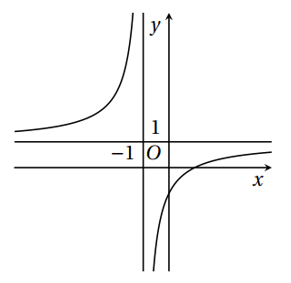
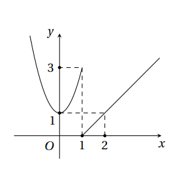
Hàm số y = f (x) có đồ thị như hình bên. Hàm số gián đoạn tại điểm có hoành độ bằng bao nhiêu?
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
Dựa vào đồ thị hàm số, hàm số gián đoạn tại điểm có hoành độ x = 1.
Câu 18:
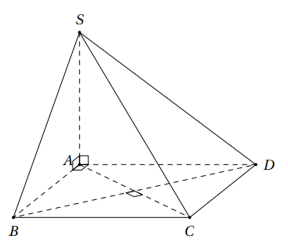
Cho hình chóp S.ABCD có đáy là hình vuông và SA vuông góc với đáy. Khẳng định nào sau đây đúng?
 Xem đáp án
Xem đáp án
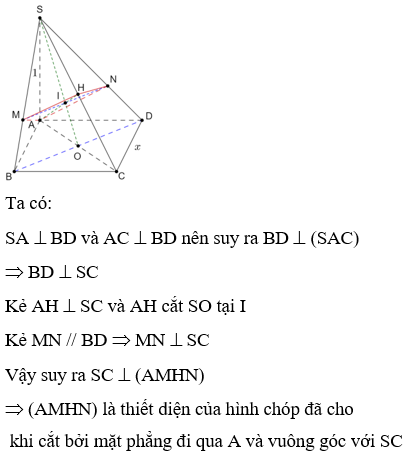
Đáp án đúng là: D
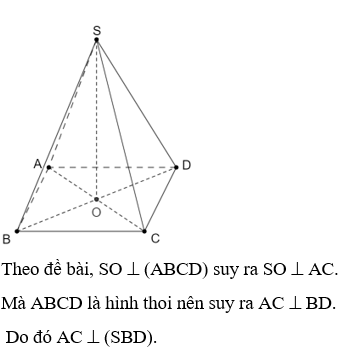
Ta có: SA ^ (ABCD) suy ra SA ^ BD.
Mà ABCD là hình vuông nên AC ^ BD.
Do đó BD ^ (SAC).
Câu 22:
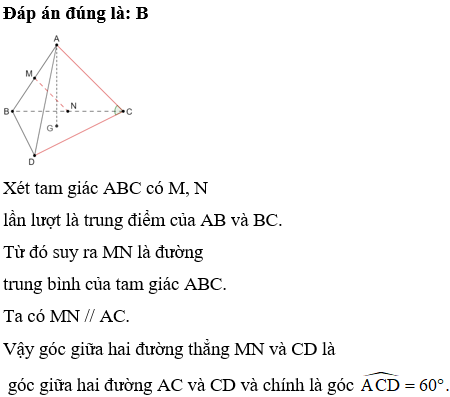
Cho tứ diện ABCD với đáy BCD là tam giác vuông cân tại C. Các điểm M, N, P, Q lần lượt là trung điểm của AB, AC, BC, CD. Góc giữa MN và PQ bằng
 Xem đáp án
Xem đáp án
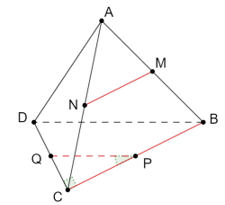
Vì M, N lần lượt là trung điểm của các cạnh AB, AC.
Nên MN là đường trung bình của tam giác ABC. Suy ra MN // BC.
Ta có MN // BC nên góc giữa MN và PQ là góc giữa BC và PQ.
Do đó góc giữa MN và PQ là .
Mà Q, P lần lượt là trung điểm của các cạnh CD, BC nên QP là đường trung bình của tam giác BCD.
Từ đó suy ra QP // BD nên góc (hai góc đồng vị và với tam giác
BCD vuông cân tại C).
Câu 32:
Cho hình chóp S.ABC có đáy là tam giác vuông tại B và SA ^ (ABC). Mệnh đề nào sau đây đúng?
 Xem đáp án
Xem đáp án
Ta có:
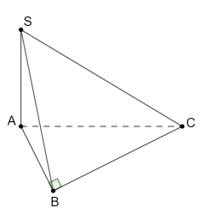
Ta có:
+) SA ^ (ABC) Þ SA ^ AB
nên tam giác SAB vuông tại A.
+) SA ^ (ABC) Þ SA ^ AC
nên tam giác SAC vuông tại A.
+) SA ^ (ABC) Þ SA ^ CB
mà AB ^ BC nên BC ^ (SAB).
Từ đó suy ra BC ^ SB
nên tam giác SCB vuông tại B.
Vậy cả 3 mặt bên của hình chóp
đã cho là các tam giác vuông.
+) SA ^ (ABC) Þ SA ^ AB
nên tam giác SAB vuông tại A.
+) SA ^ (ABC) Þ SA ^ AC
nên tam giác SAC vuông tại A.
+) SA ^ (ABC) Þ SA ^ CB
mà AB ^ BC nên BC ^ (SAB).
Từ đó suy ra BC ^ SB
nên tam giác SCB vuông tại B.
Vậy cả 3 mặt bên của hình chóp
đã cho là các tam giác vuông.
Câu 40:
Cho tứ diện ABCD có AB = CD = a. Gọi M và N lần lượt là trung điểm của AD và BC. Xác định độ dài đoạn thẳng MN để góc giữa hai đường thẳng AB và MN bằng 30°.
 Xem đáp án
Xem đáp án
Lấy P là trung điểm của AC.
Với P, N lần lượt là trung điểm của các cạnh AC, BC nên PN là đường trung bình của tam giác ABC
Nên suy ra PN // AB và .
Tương tự ta có MP // DC và .
Do đó góc giữa hai đường thẳng MN và AB chính là góc giữa hai đường thẳng MN và PN và góc đó là
Áp dụng định lý hàm cos vào tam giác MNP ta có:
Câu 41:
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
f (x) = x3 + x
Ta có đồ thị f (x) là
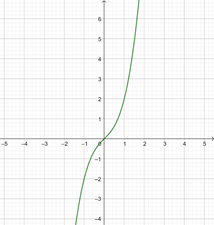
Vậy "a Î ℝ đều cho một nghiệm x.