38 câu hỏi trắc nghiệm thuộc Đề kiểm tra Giữa kì 2 Toán 11 có đáp án (Mới nhất) (Đề 15)

Câu 1:

Biết -2; a; 6 theo thứ tự đó lập thành một cấp số cộng. Giá trị của a bằng

A. -2;

B. 4;

C. 6;

D. 2

Xem đáp án

Đáp án đúng là: D

Để -2; a; 6 theo thứ tự đó lập thành một cấp số cộng thì:

(-2) + 6 = 2a

Û 2a = 4

Û a = 2.

Câu 2:

Cho cấp số cộng (u_n). Công thức nào sau đây dùng để tính tổng n số hạng đầu của cấp số cộng đã cho?

A. $S_{n} = \frac{1}{2} [2 u_{1} + (n - 1) d];$

B. $S_{n} = \frac{n}{2} [2 u_{1} + n d];$

C. $S_{n} = \frac{n}{2} [2 u_{1} + (n - 1) d];$

D. $S_{n} = \frac{n}{2} [u_{1} + (n - 1) d] .$

Xem đáp án

Đáp án đúng là: C

Công thức dùng để tính tổng n số hạng đầu của cấp số cộng đã cho là: $S_{n} = \frac{n}{2} [2 u_{1} + (n - 1) d] .$

Câu 3:

Cho cấp số cộng (u_n) có u₇ = 27 và u₂₀ = 79. Tổng 30 số hạng đầu của cấp số cộng này bằng

A. 1038;

B. 1380;

C. 1830;

D. 1083.

Xem đáp án

Đáp án đúng là: C

Công thức tổng quát các số hạng của cấp số cộng (u_n) là u_n = u₁ + (n - 1).d

Ta có: u₇ = 27 và u₂₀ = 79

Nên suy ra được hệ phương trình

. $\{\begin{matrix} u_{1} + 6 d = 27 \\ u_{1} + 19 d = 79 \end{matrix} \Leftrightarrow \{\begin{matrix} 13 d = 52 \\ u_{1} + 6 d = 27 \end{matrix} \Leftrightarrow \{\begin{matrix} d = 4 \\ u_{1} = 27 - 6 d \end{matrix} \Leftrightarrow \{\begin{matrix} d = 4 \\ u_{1} = 27 - 6.4 \end{matrix} \Leftrightarrow \{\begin{matrix} d = 4 \\ u_{1} = 3 \end{matrix}$

Từ đây ta áp dụng công thức dùng để tính tổng n số hạng đầu của cấp số cộng đã cho là: $S_{n} = \frac{n}{2} [2 u_{1} + (n - 1) d]$

Với n = 30 ta được: $S_{n} = \frac{30}{2} [2.3 + (30 - 1) .4] = 1830.$

Câu 4:

$\lim \frac{2 n - 1}{n^{3} + 5}$ bằng

A. +¥;

B. 0

C. -¥;

D. 2.

Xem đáp án

Đáp án đúng là: B

Ta có

\lim \frac{2 n - 1}{n^{3} + 5} = \lim \frac{\frac{2}{n^{2}} - \frac{1}{n^{3}}}{1 + \frac{5}{n^{3}}} = \frac{0}{1} = 1.

Câu 5:

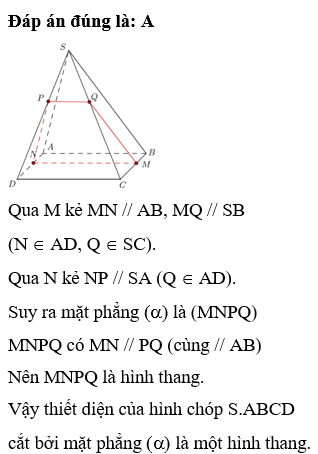
Cho hình chóp S.ABCD, có đáy ABCD là hình bình hành tâm O. Gọi M, N lần lượt là trung điểm SA, SD. Mặt phẳng (OMN) song song với mặt phẳng nào sau đây?

A. (SBC);

B. (SCD);

C. (ABCD);

D. (SAB).

Xem đáp án

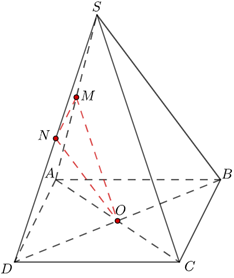
Cho hình chóp S.ABCD, có đáy ABCD là hình bình hành (ảnh 1)

Vì M, N lần lượt là trung điểm của SA, SD nên suy ra MN là đường trung bình của ∆SAD.

Từ đó MN // AD // BC Þ MN // (SBC) (1)

Vì O, N lần lượt là trung điểm của BD, SD nên suy ra ON là đường trung bình của ∆SBD.

Từ đó ON // SB Þ ON // (SBC) (2)

Từ (1) và (2) nên suy ra (OMN) // (SBC).

Câu 6:

Cho hình hộp ABCD.A’B’C’D’. Mệnh đề nào sau đây sai?

A. (ABCD) // (A’B’C’D’);

B. (AA’D’D) // (BCC’B’);

C. (ABB’A’) // (CDD’C’);

D. (BDD’B’) // (ACC’A’).

Xem đáp án

Cho hình hộp ABCD.A’B’C’D’. Mệnh đề nào sau đây sai? (ảnh 1)

Câu 7:

$\lim \frac{7 n^{2} - 3}{n^{2} - 2}$ bằng

A. $- \frac{3}{2};$

B. 7

C. $\frac{3}{2};$

D. -7

Xem đáp án

Đáp án đúng là: B

\lim \frac{7 n^{2} - 3}{n^{2} - 2} = \lim \frac{7 - \frac{3}{n^{2}}}{1 - \frac{2}{n^{2}}} = \frac{7 - 0}{1 - 0} = 7.

Câu 8:

Cho (u_n) là cấp số cộng thoả mãn u₃ + u₅ + 2u₉ = 100. Tính tổng 12 số hạng đầu của cấp số cộng.

A. S₁₂ = 300;

B. S₁₂ = 100;

C. S₁₂ = 1200;

D. S₁₂ = 600.

Xem đáp án

Công thức tổng quát các số hạng của cấp số cộng (u_n) là u_n = u₁ + (n - 1).d

u₃ + u₅ + 2u₉ = 100

Û (u₁ + 2d) + (u₁ + 4d) + 2.(u₁ + 8d) = 100

Û (u₁ + 2d) + (u₁ + 4d) + (2u₁ + 16d) = 100

Û 4u₁ + 22d = 100

Û 2u₁ + 11d = 50 (1)

Áp dụng công thức dùng để tính tổng n số hạng đầu của cấp số cộng đã cho là:

với n = 12 ta có:

= 6.(2u₁ + 11d) (2)

Thay (1) vào (2) ta được S₁₂ = 6.50 = 300.

Câu 9:

Hình chiếu của hình chữ nhật không thể là hình nào trong các hình sau?

A. Hình thang;

B. Hình bình hành;

C. Hình chữ nhật;

D. Hình thoi

Xem đáp án

Đáp án đúng là: A

Hình chiếu của hình chữ nhật không thể là hình thang

Câu 10:

Biết lim (2u_n + 3) = 0. Khi đó lim u_n bằng

A. 3

B. - 3

C. $\frac{3}{2};$

D. $- \frac{3}{2} .$

Xem đáp án

Biết lim 2un  3  0. Khi đó lim un bằng (ảnh 1)

Câu 11:

. Cho dãy số (u_n) có số hạng tổng quát $u_{n} = \frac{2 \sin (\frac{π}{3} + n π)}{2 n^{2} + 1} .$ Khi đó

A. lim u_n = 0;

B. lim u_n = +¥;

C. lim u_n = -¥;

D. lim u_n không tồn tại.

Xem đáp án

. Cho dãy số (un) có số hạng tổng quát un = 2sin(pi/3+n pi)/2n^2+1 Khi đó (ảnh 1)

Câu 12:

Trong các mệnh đề sau, mệnh đề nào sai?

A. Các cạnh bên của hình lăng trụ bằng nhau và song song với nhau;

B. Các mặt bên của hình lăng trụ là các hình bình hành;

C. Các mặt bên của hình lăng trụ là các hình bình hành bằng nhau;

D. Hai đáy của hình lăng trụ là hai đa giác bằng nhau.

Xem đáp án

Đáp án đúng là: C

+ Các cạnh bên của hình lăng trụ bằng nhau và song song với nhau (Đúng)

+ Các mặt bên của hình lăng trụ là các hình bình hành (Đúng)

+ Các mặt bên của hình lăng trụ là các hình bình hành bằng nhau (Sai vì chỉ đúng trong trường hợp lăng trụ có đáy là tam giác đều)

+ Hai đáy của hình lăng trụ là hai đa giác bằng nhau (Đúng).

Câu 13:

Cho cấp số nhân (u_n) có u₁ = 5 và công bội q = 2. Tổng của bốn số hạng đầu của cấp số nhân bằng

A. 32;

B. 75;

C. 16;

D. -75.

Xem đáp án

Cho cấp số nhân un có u1  5 và công bội q  2. Tổng của bốn số hạng đầu của cấp số nhân bằng (ảnh 1)

Câu 14:

Cho cấp số nhân (u_n) có dạng liệt kê là 3; 9; 27; 81;... Số hạng tổng quát của cấp số nhân đã cho là

A. u_n = 3^{n + 1};

B. u_n = 3ⁿ^-¹;

C. u_n = 3 + 3ⁿ^-¹;

D. u_n = 3ⁿ.

Xem đáp án

Đáp án đúng là: D

Công thức tổng quát các số hạng của cấp số nhân (u_n) là u_n = u₁.qⁿ^-¹.

Với dãy số 3; 9; 27; 81;... là các số hạng liên tiếp của cấp số nhân.

Ta có:

u_{n + 1} = u₁.qⁿ và u_{n + 2}= u₁.q^{n + 1}

Nhận thấy: 9 = 3.3; 27 = 9.3; 81 = 27.3

Suy ra q = 3

Từ đó: u_n = u₁.3ⁿ^-¹.

Chọn u₁ = 3 Þ u_n = 3ⁿ.

Câu 15:

Dãy số nào sau đây có giới hạn bằng 0?

A. $\frac{n - 1}{n + 1};$

B. $\frac{1}{2 n + 1};$

C.. n² + n;

D. 2ⁿ + 1.

Xem đáp án

Dãy số nào sau đây có giới hạn bằng 0? (ảnh 1)

Câu 16:

Dãy số $u_{n} = \frac{2 n - 13}{3 n - 2}$ là

A. Dãy số không tăng không giảm;

B. Dãy số hằng;

C. Dãy số tăng;

D. Dãy số giảm.

Xem đáp án

Câu 17:

Dãy số nào sau đây có giới hạn bằng + $\infty$ ?

A. $u_{n} = \frac{100 n + 1}{n + 2};$

B. u_n = 2ⁿ;

C. $u_{n} = \frac{2 n + 1}{n^{2} + 4};$

D. $u_{n} = {(\frac{2}{3})}^{n}$

Xem đáp án

Dãy số nào sau đây có giới hạn bằng dương vô cùng ? (ảnh 1)

Câu 18:

Cho $\lim \frac{\sqrt{8 n^{2} + 1} + 4 - 3 n}{n + 3} = a \sqrt{2} + b (a, b \in ℤ) .$ Mệnh đề nào sau đây đúng?

A. a = 3b;

B. $\sqrt{a + b + 3} < 3;$

C. 2a + b = 0;

D. a + b > 2.

Xem đáp án

Cho căn 8n^2+1+4-3n/n+3=a căn 2+b Mệnh đề nào sau đây đúng? (ảnh 1)

Câu 19:

Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M là điểm thuộc cạnh BC và (a) là mặt phẳng đi qua điểm M và song song với mặt phẳng (SAB). Thiết diện của hình chóp S.ABCD cắt bởi mặt phẳng (a) là một:

A. Hình thang;

B. Hình ngũ giác;

C. Hình tam giác;

D. Hình bình hành.

Xem đáp án

Câu 20:

Trong các dãy số sau, dãy số nào là dãy số giảm?

A. 1; 0; -1; -2; -3

B. $1; - \frac{1}{2}; \frac{1}{4}; - \frac{1}{8}; \frac{1}{16};$

C. 1; 1; 1; 1; 1;

D. 1; 3; 5; 7; 9.

Xem đáp án

Đáp án đúng là: A

Dễ dàng nhận thấy 1; 0; -1; -2; -3 là dãy số giảm.

Câu 21:

Cho cấp số cộng (u_n) thoả mãn $\{\begin{matrix} u_{1} + u_{2} + 3 u_{3} = 19 \\ 3 u_{2} - u_{5} + u_{8} = 15 \end{matrix} .$ Số hạng đầu u₁ và công sai d của cấp số cộng đã cho lần lượt là

A. u₁ = 1; d = 2;

B. u₁ = -1; d = -2;

C. u₁ = 2; d = 1;

D. u₁ = -2; d = -1.

Xem đáp án

Cho cấp số cộng un thoả mãn u1+u2+3u3=19 Số hạng đầu u1 (ảnh 1)

Câu 22:

Cho dãy số (u_n): $\{\begin{matrix} u_{1} = 2 \\ u_{n + 1} = u_{n} + 3; \forall n = 1, 2, ... \end{matrix} .$ Giá trị của u₃ bằng

A. 2

B. 5;

C. 3

D. 8.

Xem đáp án

Cho dãy số (un): u1=2 un+2=un+2=un+3 Giá trị của u3 bằng (ảnh 1)

Câu 23:

Dãy số nào dưới đây là một cấp số nhân hữu hạn?

A. $1; \frac{1}{2}; \frac{1}{4}; \frac{1}{6}; \frac{1}{8};$

B. 1; 3; 6; 9; 12

C. 1; 3; 9; 27; 81;

D. 6; 5; 4; 3; 2.

Xem đáp án

Đáp án đúng là: A

Dãy số $1; \frac{1}{2}; \frac{1}{4}; \frac{1}{6}; \frac{1}{8}$ có công thức số hạng tổng quát là $u_{n} = \frac{1}{2^{n - 1}} \Rightarrow \lim u_{n} = \lim \frac{1}{2^{n - 1}} = 0$

Nên đây là một cấp số nhân hữu hạn.

Câu 24:

Cho cấp số cộng (u_n) có u₁ = 2 và công sai d = 5. Mệnh đề nào sau đây đúng?

A. u₃ = -3;

B. u₂ = -3;

C. u₃ = 7;

D. u₂ = 7.

Xem đáp án

Đáp án đúng là: D

Công thức tổng quát các số hạng của cấp số cộng (u_n) là:

u_n = u₁ + (n - 1).d

Với u₁ = 2, d = 5 ta có: u_n = 2 + (n - 1).5

Từ đây ta có:

u₂ = 2 + (2 - 1).5 = 7;

u₃ = 2 + (3 - 1).5 = 12.

Vậy mệnh đề đúng là u₂ = 7.

Câu 25:

Cho dãy số: -1; x; 0,36. Tìm x để dãy số đã cho theo thứ tự lập thành cấp số nhân.

A. Không có giá trị nào của x.

B. x = -0,008;

C. x = 0,008;

D. x = 0,004.

Xem đáp án

Đáp án đúng là: A

Để dãy số đã cho theo thứ tự lập thành cấp số nhân thì

(-1).0,36 = x²

Û x²= -0,36 (vô lý)

Vậy không có giá trị nào của x.

Câu 26:

Cho cấp số nhân có u₁ = -3, $q = \frac{2}{3} .$ Số $\frac{- 96}{243}$ là số hạng thứ mấy của cấp số này?

A. Thứ 5

B. Thứ 7;

C. Thứ 6;

D. Không phải là số hạng của cấp số

Xem đáp án

Cho cấp số nhân có u1 = 3, Số là số hạng thứ mấy của cấp số này? (ảnh 1)

Câu 27:

Hãy chọn mệnh đề đúng trong các mệnh đề sau đây?

A. Hai mặt phẳng phân biệt không song song thì cắt nhau;

B. Nếu hai mặt phẳng song song thì mọi đường thẳng nằm trong mặt phẳng này đều song song với mọi đường thẳng nằm trong mặt phẳng kia;

C. Hai mặt phẳng cùng song song với một đường thẳng thì song song với nhau;

D. Nếu hai mặt phẳng (P) và (Q) lần lượt chứa hai đường thẳng song song thì song song với nhau.

Xem đáp án

Đáp án đúng là: A

+ Hai mặt phẳng phân biệt không song song thì cắt nhau (Đúng)

+ Nếu hai mặt phẳng song song thì mọi đường thẳng nằm trong mặt phẳng này đều song song với mọi đường thẳng nằm trong mặt phẳng kia (Sai vì hai đường thẳng có thể chéo nhau hoặc vuông góc với nhau)

+ Hai mặt phẳng cùng song song với một đường thẳng thì song song với nhau (Sai vì hai mặt phẳng có thể vuông góc với nhau hoặc trùng nhau)

+ Nếu hai mặt phẳng (P) và (Q) lần lượt chứa hai đường thẳng song song thì song song với nhau (Sai vì hai mặt phẳng có thể cắt nhau).

Câu 28:

$\lim \frac{99^{n} + {3.100}^{n}}{100^{n + 1} - 1}$ bằng

A. $\frac{99}{100};$

B. 3

C. $\frac{3}{100};$

D. 99

Xem đáp án

Câu 29:

$\lim \frac{2 n^{2} - n + 1}{2 n - 1}$ bằng

A. 1;

B. -¥;

C. 0;

D. +¥.

Xem đáp án

Câu 30:

Cho cấp số nhân (u_n) có u₄ = 6, u₅ = 2. Tìm công bội q của cấp số nhân.

A. q = 4;

C.

B. q = 3;

C. $q = \frac{1}{3};$

D. q = -4.

Xem đáp án

Đáp án đúng là: C

Công thức tổng quát các số hạng của cấp số nhân (u_n) là u_n = u₁.qⁿ^-¹.

Ta có u₄ = 6, u₅ = 2 nên suy ra được hệ phương trình

. $\{\begin{matrix} u_{1} . q^{3} = 6 \\ u_{1} . q^{4} = 2 \end{matrix} \Leftrightarrow \{\begin{matrix} u_{1} . q^{3} = 6 \\ q = \frac{2}{6} = \frac{1}{3} \end{matrix} \Leftrightarrow \{\begin{matrix} u_{1} = \frac{6}{q^{3}} \\ q = \frac{1}{3} \end{matrix} \Leftrightarrow \{\begin{matrix} u_{1} = 162 \\ q = \frac{1}{3} \end{matrix}$

Vậy công bội của cấp số nhân là $q = \frac{1}{3}$ .

Câu 31:

Cho một đường thẳng a song song với mặt phẳng (P). Có bao nhiêu mặt phẳng chứa a và song song với (P)?

A. 1;

B. 2;

C. vô số;

D. 0.

Xem đáp án

Đáp án đúng là: A

Qua một đường thẳng a song song với mặt phẳng (P) chỉ có duy nhất một mặt phẳng chứa a và song song với (P).

Câu 32:

Cho hai đường thẳng a và b lần lượt nằm trên hai mặt phẳng (P) và (Q). Mệnh đề nào sau đây đúng?

A. Nếu (P) // (Q) thì a // b;

B. Nếu (P) // (Q) thì a // (Q);

C. Nếu a // b thì (P) // (Q);

D. Nếu a // (Q) thì a // b.

Xem đáp án

Đáp án đúng là: B

+ Nếu (P) // (Q) thì a // b (Sai vì a, b có thể vuông góc và chéo nhau)

+ Nếu (P) // (Q) thì a // (Q) (Đúng)

+ Nếu a // b thì (P) // (Q) (Sai vì hai mặt phẳng có thể cắt nhau, vuông góc và trùng nhau)

+ Nếu a // (Q) thì a // b (Sai vì a và b có thể chéo

Câu 33:

Cho hình chóp S.ABC. Gọi I, J, K lần lượt là trọng tâm các tam giác SAB, SBC, SAC. Mệnh đề nào sau đây đúng?

A. (IJK) song song với (ABC);

B. (IJK) trùng (ABC);

C. (IJK) và (ABC) có đúng một điểm chung;

D. (IJK) và (ABC) một đường thẳng chung.

Xem đáp án

Đáp án đúng là: A

Gọi M, N, P lần lượt là trung điểm các cạnh AB, BC, AC.

Vì IJ // MN nên IJ // (ABC).

Lại có IK // MP suy ra IK // (ABC).

Suy ra (IJK) song song với (ABC).

Câu 34:

Biết $\lim \frac{(a - 1) n^{2} + 2 n - 3}{2 n^{2} + a^{2} - a} = 3$ (a Î ℝ cho trước). Mệnh đề nào sau đây đúng?

A. a Î (2; 5);

B. a Î (3; 6);

C. a Î (7; +¥);

D. a Î (6; 9).

Xem đáp án

Biết lim(a-1)n^2+2n-3/2n^2+a^2-a (a thuộc ℝ cho trước). Mệnh đề nào sau (ảnh 1)

Câu 35:

Cho hình hộp ABCD.A’B’C’D. Mặt phẳng (AB’D’) song song với mặt phẳng nào trong các mặt phẳng sau đây?

A. (BCA’).

B. (BC’D);

C. (A’C’C);

D. (BDA’)

Xem đáp án

Đáp án đúng là: B

Ta có: AB’ // DC’ Þ DC’ // (AB’D’)

Lại có BD // B’D’ Þ BD // (AB’D’)

Suy ra (BC’D) // (AB’D’).

Câu 36:

Tính giới hạn $\lim \frac{3 n^{2} - 2 n - 1}{1 + 3 n - 5 n^{2}} .$

Xem đáp án

Tính giới hạn lim3n^2-2n-1/1+3n-5n^2 (ảnh 1)

Câu 37:

Cho hình lăng trụ tam giác ABC.A’B’C’.

a) Gọi E, F lần lượt là tâm của các mặt bên ABB’A’ và ACC’A’. Chứng minh đường

thẳng EF song song mặt phẳng (BCC’B’).

b) Gọi G là trọng tâm của tam giác ABC và H là trung điểm của B’C’. Chứng minh đường thẳng C’G song song với mặt phẳng (A’BH).

Xem đáp án

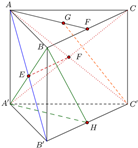
Cho hình lăng trụ tam giác ABC.A’B’C’. a) Gọi E, F lần lượt là tâm của các mặt bên ABB’A’ (ảnh 1)

a) Ta có: E, F lần lượt là tâm của các hình bình hành ABB’A’ và ACC’A’.

Nên E và F lần lượt là trung điểm của các cạnh AB’ và AC’.

Xét ∆AB’C’ có E, F lần lượt là trung điểm của các cạnh AB’ và AC’.

Từ đó ta có EF là đường trung bình của ∆AB’C’.

Suy ra EF // B’C’.

Từ đó đường thẳng EF song song mặt phẳng (BCC’B’) .

b) Lấy F là trung điểm của BC .

Ta có AF // A’H Þ AF // (A’BH)

Và C’F // BH Þ C’F // (A’BH)

Suy ra (C’FA) // (A’BH).

Mà C’G Î (C’FA) Þ C’G // (A’BH).

Câu 38:

Cho dãy số (u_n) có $\{\begin{matrix} u_{1} = 4 \\ u_{n + 1} = 3 u_{n} + 4; \forall n = 1, 2, 3... \end{matrix} .$ Tính $\lim \frac{u_{n} + 2^{n}}{2^{n + 1} - 3} .$

Xem đáp án

Đề kiểm tra Giữa kì 2 Toán 11 có đáp án (Mới nhất)

Đề kiểm tra Giữa kì 2 Toán 11 có đáp án (Mới nhất) (Đề 15)

Danh sách câu hỏi

Bài thi liên quan

Có thể bạn quan tâm

Các bài thi hot trong chương