35 câu hỏi trắc nghiệm thuộc Đề kiểm tra Giữa kì 2 Toán 11 có đáp án (Mới nhất) (Đề 3)

Câu 1:

Mệnh đề nào sau đây là đúng?

A. $\lim \frac{1}{n} = + \infty$

B. $\lim (- 2 n + 1) = - \infty$

C. $\lim \frac{2 - n}{3 n^{2}} = - \infty$

D. $\lim \frac{- 3}{- 2 n + 1} = \frac{3}{2}$

Xem đáp án

Chọn B

Ta có: $\lim (- 2 n + 1) = \lim n (- 2 + \frac{1}{n})$ $= - \infty$ .

Câu 2:

Tính $\lim (- n^{2} + 4)$ ?

A. $+ \infty$ .

B. $- \infty$ .

C. -1.

D. 4.

Xem đáp án

Chọn A

Ta có $\lim (n^{2} + 4) = \lim [n^{2} . (- 1 + \frac{4}{n^{2}})]$ $= - \infty$ .

Câu 3:

Cho các dãy số

(u_{n}), (v_{n})

và

{limu}_{n} = a,

{limv}_{n} = + \infty

thì

\lim \frac{u_{n}}{v_{n}}

bằng

A. 1.

B. 0.

C. $+ \infty$ .

D. $- \infty$

Xem đáp án

Chọn B

Dùng tính chất giới hạn: cho dãy số $(u_{n}), (v_{n})$ và ${limu}_{n} = a,$ ${limv}_{n} = + \infty$ trong đó a hữu hạn thì $\lim \frac{u_{n}}{v_{n}} = 0$

Câu 4:

Tính $\lim \frac{2 n + 1}{1 + n}$ được kết quả là

A. 2.

B. 0.

C. $\frac{1}{2}$ .

D. 1

Xem đáp án

Chọn A

Ta có

lim \frac{2 n + 1}{1 + n} = \lim \frac{n (2 + \frac{1}{n})}{n (\frac{1}{n} + 1)}

= \lim \frac{2 + \frac{1}{n}}{\frac{1}{n} + 1}

= \frac{2 + 0}{0 + 1}

= 2

Câu 5:

Dãy số nào sau đây có giới hạn bằng 0?

A. ${(\frac{1}{3})}^{n}$

B. ${(\frac{4}{e})}^{n}$

C. ${(\frac{- 5}{3})}^{n}$

D. ${(\frac{5}{3})}^{n}$

Xem đáp án

Chọn A

Ta có: nếu |q| < 1 thì $\lim q^{n} = 0$ .

Trong các đáp án, chỉ có $|\frac{1}{3}| < 1$ nên $\lim {(\frac{1}{3})}^{n} = 0$ .

Câu 6:

Cho hai dãy số $(u_{n}), (v_{n})$ thỏa mãn $\lim u_{n} = 9$ và $\lim v_{n} = 2$ Giá trị của $\lim (u_{n} . v_{n})$ bằng

A. 18

B. 7

C. 11

D. -7

Xem đáp án

Chọn A

Ta có: $\lim (u_{n} . v_{n}) = 9 .2 = 18$

Câu 7:

Cho dãy số $(u_{n})$ thỏa mãn $\lim u_{n} = 15 .$ Giá trị của $lim (u_{n} - 2)$ bằng

A. 13

B. -13

C. 30

D. -30

Xem đáp án

Chọn A

Ta có: $\lim (u_{n} - 2) = 15 - 2 = 13$ .

Câu 8:

\lim_{x \to 9} \sqrt{x + 16}

bằng

A. 5

B. 4

C. 25

D. 9

Xem đáp án

Chọn A

Ta có: $\lim_{x \to 9} \sqrt{x + 16} = \sqrt{25} = 5$ .

Câu 9:

Cho hai hàm số f(x), g(x) thỏa mãn

\lim_{x \to 1} f (x) = 5

và

\lim_{x \to 1} g (x) = 2 .

Giá trị của

\lim_{x \to 1} [f (x) - g (x)]

bằng

A. 3

B. 10

C. -3

D. 3

Xem đáp án

Chọn A

Ta có:

\lim_{x \to 1} [f (x) - g (x)] = 5 - 2 = 3

Câu 10:

Cho hàm số f(x) thỏa mãn

\lim_{x \to 1^{+}} f (x) = 2021

và

\lim_{x \to 1^{-}} f (x) = 2021 .

Giá trị của

\lim_{x \to 1} f (x)

bằng

A. 2021

B. 1

C. 2020

D. 2022

Xem đáp án

Chọn A

Ta có: $\lim_{x \to 1} f (x) = 2021$ .

Câu 11:

Giá trị của $\lim_{x \to 1} (2 x^{2} - 3 x + 1)$ bằng

A. 2

B. 1

C. $+ \infty$

D. 0

Xem đáp án

Chọn D

Ta có: $\lim_{x \to 1} (2 x^{2} - 3 x + 1) = 0$ .

Câu 12:

\lim_{x \to + \infty} x^{2021}

bằng

A. $+ \infty .$

B. $- \infty .$

C. 0

D. 1

Xem đáp án

Chọn A

Ta có: $\lim_{x \to + \infty} x^{2021} = + \infty$

Câu 13:

Cho hai hàm số f(x), g(x) thỏa mãn

\lim_{x \to 1} f (x) = 2021

và

\lim_{x \to 1} g (x) = + \infty .

Giá trị của

\lim_{x \to 1} [f (x) . g (x)]

bằng

A. $+ \infty$

B. $- \infty$

C. 2

D. -2

Xem đáp án

Chọn A

Ta có: $\lim_{x \to 1} [f (x) . g (x)] = + \infty$

Câu 14:

Hàm số $y = \frac{1}{x - 2022}$ gián đoạn tại điểm nào dưới đây?

A. x = 2022

B. x = 2020

C. x = 2023

D. x = -2022

Xem đáp án

Chọn A

Ta có: $\lim_{x \to 2022^{+}} \frac{1}{x - 2022} \neq \lim_{x \to 2022^{-}} \frac{1}{x - 2022}$ . Nên hàm số $y = \frac{1}{x - 2022}$ gián đoạn tại điểm x = 2022.

Câu 15:

Hàm số $y = \frac{2021}{(x - 1) (x - 2) (x - 3)}$ liên tục tại điểm nào dưới đây?

A. x = -2

B. x = 3

C. x = 1

D. x = 2

Xem đáp án

Chọn A

Ta có: $\lim_{x \to - 2} \frac{2021}{(x - 1) (x - 2) (x - 3)} = f (- 2)$ . Hàm số $y = \frac{2021}{(x - 1) (x - 2) (x - 3)}$ liên tục tại x = -2.

Câu 16:

Hình chiếu của hình chữ nhật không thể là hình nào trong các hình sau?

A. Hình thang

B. Hình bình hành

C. Hình chữ nhật

D. Hình thoi

Xem đáp án

Chọn A

Do phép chiếu song song biến hai đường thẳng song song thành hai đường thẳng song song hoặc trùng nhau, nên không thể có đáp án A

Câu 17:

Cho tứ diện ABCD. Gọi M, N lần lượt là trung điểm của AD và BC. Khẳng định nào sau đây sai?

A. $\vec{AB} + \vec{CD} = \vec{CB} + \vec{AD}$

B. $2 \vec{MN} = \vec{AB} + \vec{DC}$

C. $\vec{AD} + 2 \vec{MN} = \vec{AB} + \vec{AC}$

D. $2 \vec{MN} = \vec{AB} + \vec{AC} + \vec{AD}$

Xem đáp án

Chọn D

Ta có N là trung điểm của BC nên $2 \vec{MN} = \vec{MB} + \vec{MC}$ $= \vec{MA} + \vec{AB} + \vec{MA} + \vec{AC} =$ $2 \vec{MA} + \vec{AB} + \vec{AC} =$ $\vec{DA} + \vec{AB} + \vec{AC} =$ $- \vec{AD} + \vec{AB} + \vec{AC}$

(Vì M là trung điểm AD).

Câu 18:

Cho hình hộp ABCD.A'B'C'D'. Ta có

\vec{BA} + \vec{BC} + \vec{{BB}^{'}}

bằng

A. $\vec{BD'}$

B. $\vec{BD}$

C. $\vec{BA'}$

D. $\vec{BC'}$

Xem đáp án

Chọn A

Theo quy tắc hình hộp ta có $\vec{BA} + \vec{BC} + \vec{{BB}^{'}} = \vec{{BD}^{'}}$ .

Câu 19:

Với hai vectơ $\vec{u}, \vec{v}$ khác vectơ - không tùy ý, tích vô hướng $\vec{u} . \vec{v}$ bằng

A. $|\vec{u}| . |\vec{v}| . \cos (\vec{u}, \vec{v})$

B. $- |\vec{u}| . |\vec{v}| . \cos (\vec{u}, \vec{v})$

C. $|\vec{u}| . |\vec{v}| . \cot (\vec{u}, \vec{v})$

D. $- |\vec{u}| . |\vec{v}| . \cot (\vec{u}, \vec{v})$

Xem đáp án

Chọn A

Ta có: $\vec{u} . \vec{v} = |\vec{u}| . |\vec{v}| . \cos (\vec{u}, \vec{v})$ .

Câu 20:

Cho hình lập phương ABCD.A'B'C'D'. Số đo của góc giữa hai đường thẳng AB và DD' là

A. $90^{0}$

B. $60^{0}$

C. $45^{0}$

D. $120^{0}$

Xem đáp án

Chọn A

Do ${DD}^{'} ⊥ (ABCD)$ nên ${DD}^{'} ⊥ AB$ $\Rightarrow (AB; {DD}^{'}) = 90 °$ .

Câu 21:

$\lim \frac{3 n - 2}{n + 3}$ bằng

A. $\frac{- 2}{3}$

B. 1

C. 3

D. -2

Xem đáp án

Chọn C

Ta có: $\lim \frac{3 n - 2}{n + 3} = = \lim \frac{3 - \frac{2}{n}}{1 + \frac{3}{n}} = 3$ .

Câu 22:

Cho cấp số nhân lùi vô hạn có

u_{1} = 1

và công bội

q = - \frac{1}{2}

. Tổng S của cấp số nhân lùi vô hạn đã cho bằng

A. S = 2

B. S = $\frac{3}{2}$

C. S = 1

D. S = $\frac{2}{3}$

Xem đáp án

Chọn D

$S = \frac{u_{1}}{1 - q} = \frac{1}{1 + \frac{1}{2}} = \frac{2}{3}$ .

Câu 23:

\lim \frac{3 {.2}^{n} - 3^{n}}{2^{n + 1} + 3^{n + 1}}

bằng

A. $\frac{- 1}{3}$

B. $- \infty$

C. 2

D. 1

Xem đáp án

Chọn A

$K = \lim \frac{3 {(\frac{2}{3})}^{n} - 1}{2 {(\frac{2}{3})}^{n} + 3} = - \frac{1}{3}$

Câu 24:

\lim_{x \to + \infty} (- x^{3} + x^{2} + 2021)

bằng

A. 0

B. $- \infty$

C. $+ \infty$

D. 2

Xem đáp án

Chọn B

Ta có:

\lim_{x \to + \infty} (- x^{3} + x^{2} + 2021)

= \lim_{x \to + \infty} [(x^{3}) . (- 1 + \frac{1}{x} + \frac{2021}{x^{3}})]

= - \infty

Câu 25:

\lim_{x \to 1^{-}} \frac{x + 2022}{x - 1}

bằng

A. 0

B. $+ \infty$

C. 1

D. $- \infty$

Xem đáp án

Chọn D

$\lim_{x \to 1^{-}} \frac{x + 2022}{x - 1} = - \infty$ do $\lim_{x \to 1^{-}} (x + 2022) = 2023 > 0$ , $\lim_{x \to 1^{-}} (x - 1) = 0 và (x - 1) < 0$ với x < 1.

Câu 26:

\lim_{x \to - 2} \frac{2 x^{2} + 3 x - 2}{x^{2} - 4}

bằng

A. $\frac{5}{4}$

B. $\frac{- 5}{4}$

C. $\frac{1}{4}$

D. 2

Xem đáp án

Chọn A

Ta có $\lim_{x \to - 2} \frac{2 x^{2} + 3 x - 2}{x^{2} - 4}$ $= \lim_{x \to - 2} \frac{(2 x - 1) (x + 2)}{(x - 2) (x + 2)}$ $= \lim_{x \to - 2} \frac{2 x - 1}{x - 2} = \frac{5}{4}$ .

Câu 27:

Hàm số

f (x) = \frac{x^{2} + 1}{x^{2} + 5 x + 6}

liên tục trên khoảng nào dưới đây?

A. (-3;2)

B. $(- 2; + \infty)$

C. $(- \infty; 3)$

D. (2;3)

Xem đáp án

Chọn B

Hàm số có nghĩa khi $x^{2} + 5 x + 6 \neq 0$ $\Leftrightarrow \{\begin{cases} x \neq - 3 \\ x \neq - 2 \end{cases}$ .

Vậy theo định lí ta có hàm số

f (x) = \frac{x^{2} + 1}{x^{2} + 5 x + 6}

liên tục trên khoảng

(- \infty; - 3)

; (-3;-2) và

(- 2; + \infty)

.

Câu 28:

Cho hàm số

f (x) = \{\begin{cases} \frac{\sqrt{3 x + 1} - 2}{x - 1} khi x \neq 1 \\ m khi x = 1 \end{cases}

. Giá trị của tham số m để hàm số f(x) liên tục tại điểm x = 1 bằng

A. m = 3

B. m = 1

C. m = $\frac{3}{4}$

D. m = $\frac{1}{2}$

Xem đáp án

Chọn C

Ta có $\lim_{x \to 1} \frac{\sqrt{3 x + 1} - 2}{x - 1}$ $= \lim_{x \to 1} \frac{3 x + 1 - 2^{2}}{(x - 1) (\sqrt{3 x + 1} + 2)}$ $= \lim_{x \to 1} \frac{3}{\sqrt{3 x + 1} + 2} = \frac{3}{4}$ .

Với f(1) = m ta suy ra hàm số liện tục tại x = 1 khi m = $\frac{3}{4}$ .

Câu 29:

Hàm số nào dưới đây liên tục trên khoảng (0; 2021) ?

A. $y = \frac{x - 2}{x + 2020}$

B. $y = \frac{2 x + 1}{x - 25}$

C. $y = \frac{x + 1}{x - 2020}$

D. $y = \frac{1}{x^{2} - 4}$

Xem đáp án

Chọn A

Ta có hàm số

y = \frac{x - 2}{x + 2020}

luôn xác định trên khoảng (0;2021).

Câu 30:

Trong các hàm số sau, hàm số nào liên tục trên $(- \infty; + \infty)$ ?

A. f(x) = tan x + 5

B. $f (x) = \frac{x^{2} + 3}{5 - x}$

C. $f (x) = \sqrt{x - 6}$

D. $f (x) = \frac{x + 5}{x^{2} + 4}$

Xem đáp án

Chọn D

Hàm số

f (x) = \frac{x + 5}{x^{2} + 4}

là hàm phân thức hữu tỉ và có TXĐ là D =

ℝ

do đó hàm số

f (x) = \frac{x + 5}{x^{2} + 4}

liên tục trên

ℝ

.

Câu 31:

Cho hình lập phương ABCD.A'B'C'D'. Tính góc giữa hai đường thẳng B'D' và AA'.

A. $90^{0}$

B. $45^{0}$

C. $60^{0}$

D. $30^{0}$

Xem đáp án

Chọn A

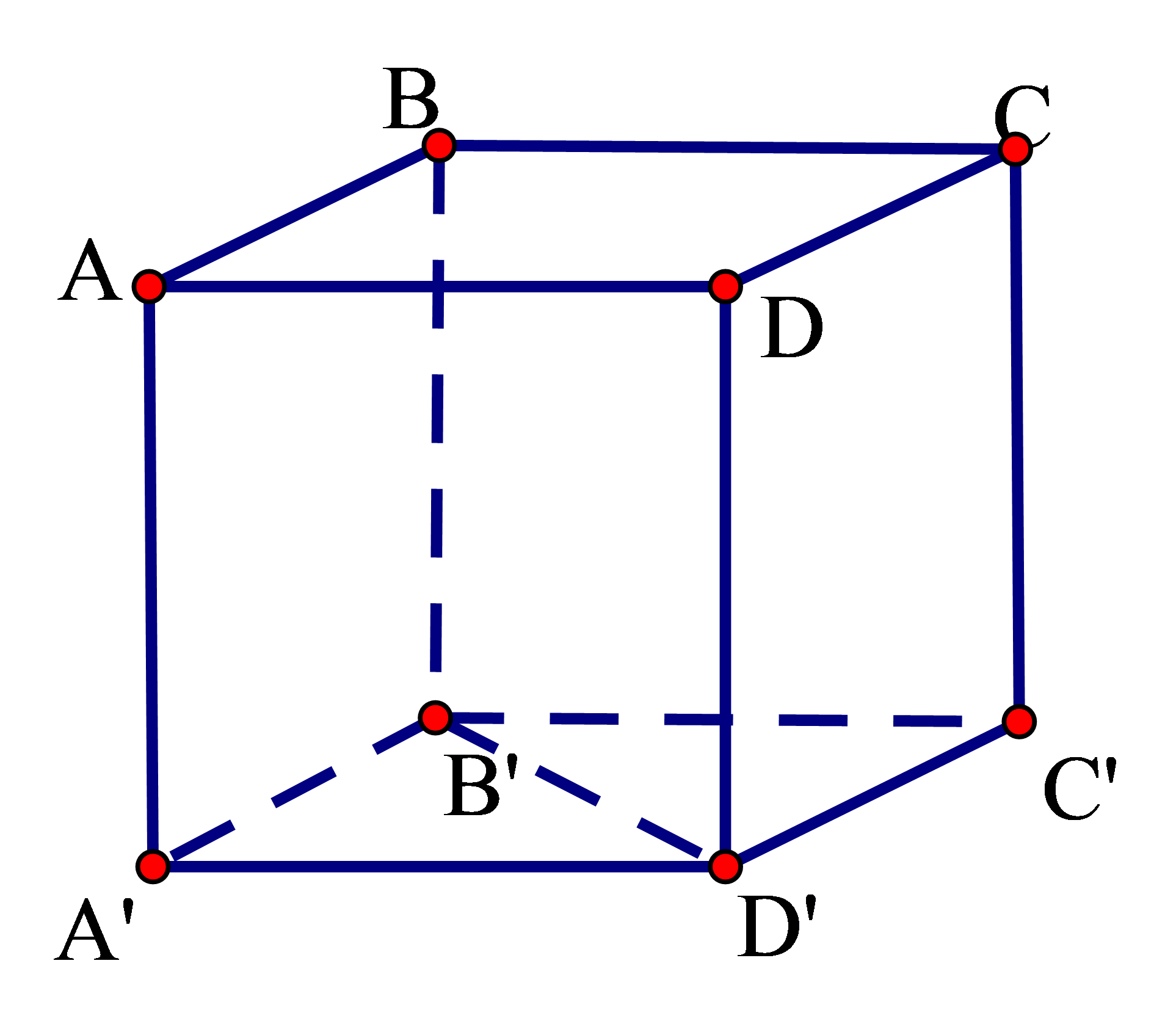
Ta có ABCD.A'B'c'D' là hình lập phương nên cạnh $A^{'} A ⊥ (A^{'} B^{'} C^{'} D^{'})$ và $B^{'} D^{'} \in (A^{'} B^{'} C^{'} D^{'})$

Nên $A^{'} A ⊥ B^{'} D^{'}$ $\Rightarrow ∡ (A^{'} A, B^{'} D^{'}) = 90 °$ .

Câu 32:

Cho tứ diện đều ABCD. Số đo góc giữa hai đường thẳng AB và CD bằng:

A. $60^{0}$

B. $30^{0}$

C. $90^{0}$

D. $45^{0}$

Xem đáp án

Chọn C

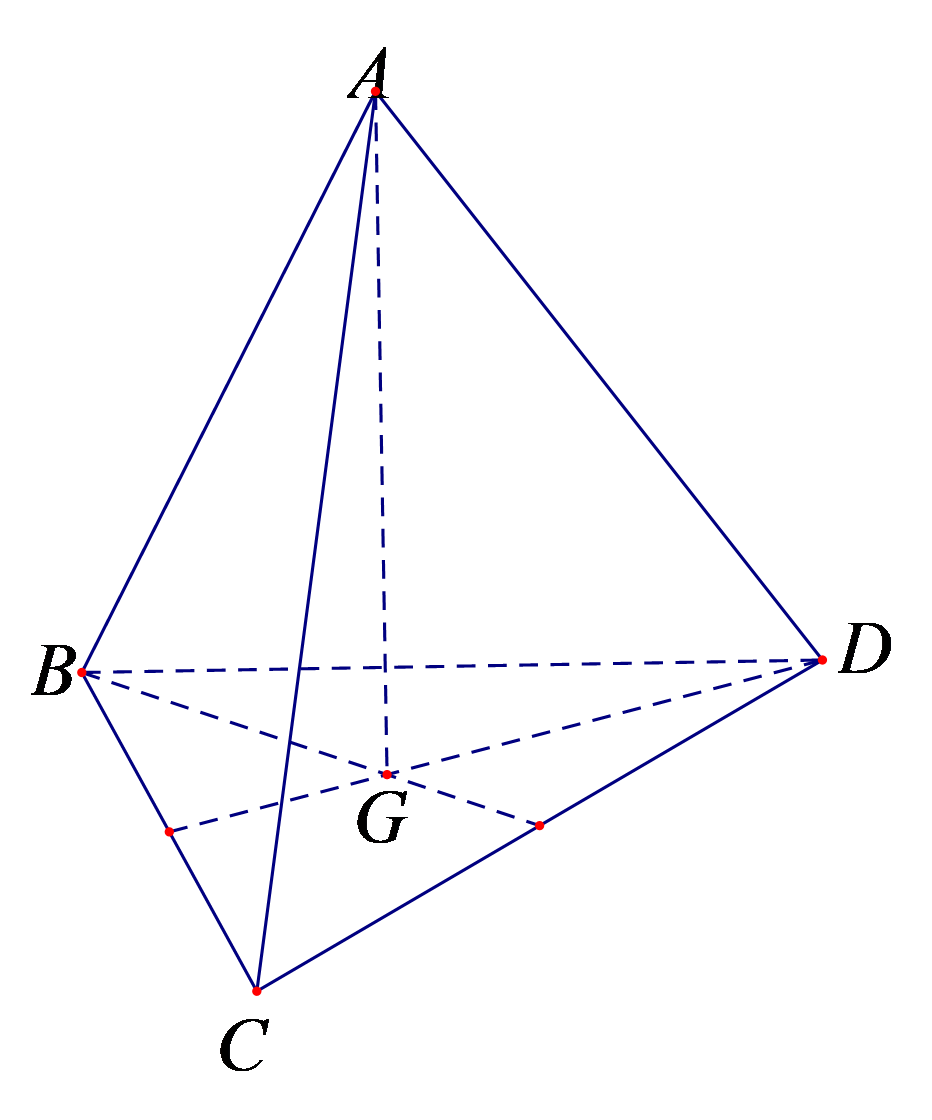
Gọi G là trọng tâm tam giác ABC.

Vì tứ diện ABCD đều nên $AG ⊥ (BCD)$ .

Ta có: $\{\begin{cases} CD ⊥ AG \\ CD ⊥ BG \end{cases}$ $\Rightarrow CD ⊥ (ABG)$ $\Rightarrow CD ⊥ AB$ .

Vậy số đo góc giữa hai đường thẳng AB và CD bằng $90^{0}$ .

Câu 33:

Cho hai vectơ

\vec{a}, \vec{b}

thỏa mãn:

|\vec{a}| = 4;

|\vec{b}| = 3;

|\vec{a} - \vec{b}| = 4

. Gọi

α

là góc giữa hai vectơ

\vec{a}, \vec{b}

. Chọn khẳng định đúng?

A. $cosα = \frac{3}{8}$

B. $α = 30 °$

C. $cosα = \frac{1}{3}$

D. $α = 60 °$

Xem đáp án

Chọn A

{(\vec{a} - \vec{b})}^{2} = {|\vec{a}|}^{2} + {|\vec{b}|}^{2} - 2 \vec{a} . \vec{b}

\Rightarrow \vec{a} . \vec{b} = \frac{9}{2} .

Do đó: $\cos α = \frac{\vec{a} . \vec{b}}{|\vec{a}| . |\vec{b}|} = \frac{3}{8}$ .

Câu 34:

Cho hình tứ diện ABCD có trọng tâm G. Mệnh đề nào sau đây sai.

A. $\vec{AG} = \frac{2}{3} (\vec{AB} + \vec{AC} + \vec{AD})$

B. $\vec{AG} = \frac{1}{4} (\vec{AB} + \vec{AC} + \vec{AD})$

C. $\vec{OG} = \frac{1}{4} (\vec{OA} + \vec{OB} + \vec{OC} + \vec{OD})$

D. $\vec{GA} + \vec{GB} + \vec{GC} + \vec{GD} = \vec{0}$

Xem đáp án

Chọn A

Theo giả thuyết trên thì với O là một điểm bất kỳ ta luôn có: $\vec{OG} = \frac{1}{4} (\vec{OA} + \vec{OB} + \vec{OC} + \vec{OD})$ .

Ta thay điểm O bởi điểm A thì ta có: $\vec{AG} = \frac{1}{4} (\vec{AA} + \vec{AB} + \vec{AC} + \vec{AD})$ $\Leftrightarrow \vec{AG} = \frac{1}{4} (\vec{AB} + \vec{AC} + \vec{AD})$

Do vậy $\vec{AG} = \frac{2}{3} (\vec{AB} + \vec{AC} + \vec{AD})$ là sai.

Câu 35:

Cho tứ diện ABCD. Gọi E là trung điểm AD, F là trung điểm BC và G là trọng tâm của tam giác BCD.Tìm mệnh đề sai trong các mệnh đề sau:

A. $\vec{EB} + \vec{EC} + \vec{ED} = 3 \vec{EG}$

B. $\vec{GA} + \vec{GB} + \vec{GC} + \vec{GD} = \vec{0}$

C. $\vec{AB} + \vec{AC} + \vec{AD} = 3 \vec{AG}$

D. $2 \vec{EF} = \vec{AB} + \vec{DC}$

Xem đáp án

Chọn B

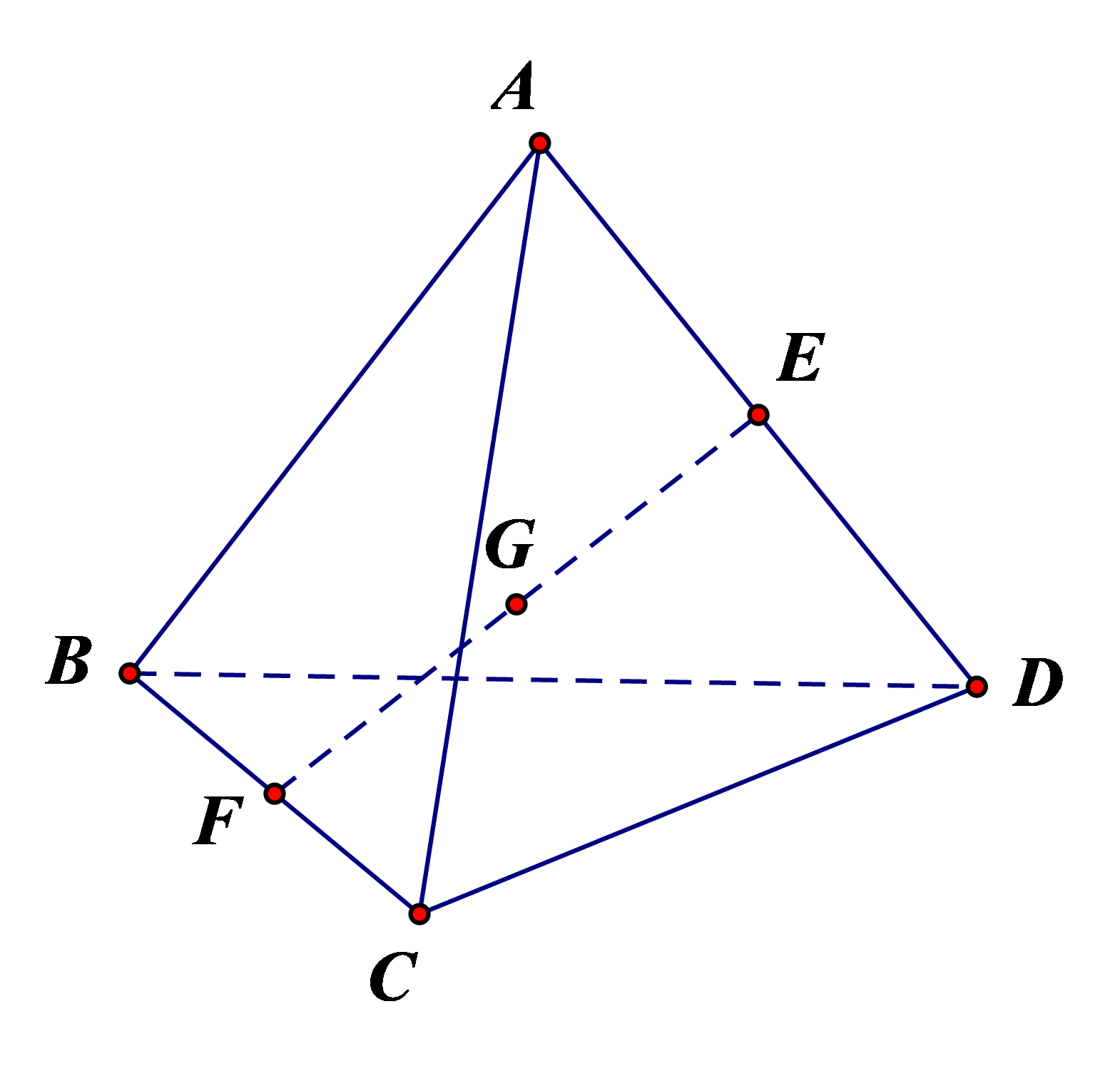
Do G là trọng tâm tam giác BCD nên với điểm M bất kỳ ta có: $\vec{MB} + \vec{MC} + \vec{MD} = 3 \vec{MG}$ .

* Thay M bằng E ta được phương án A => A đúng.

* Do G là trọng tâm tam giác BCD nên $\vec{GB} + \vec{GC} + \vec{GD} = \vec{0}$ => B sai vì $\vec{GD} \neq \vec{0}$ $do G \equiv D$ .

* Thay M bằng A ta được phương án C => C sai.

* Do E là trung điểm AD, F là trung điểm BC nên: $\vec{EA} + \vec{ED} = \vec{0}$ ; $\vec{FB} + \vec{FC} = - (\vec{BF} + \vec{CF}) = \vec{0}$ .

Có $\{\begin{cases} \vec{AB} = \vec{AE} + \vec{EF} + \vec{FB} \\ \vec{DC} = \vec{DE} + \vec{EF} + \vec{FB} \end{cases}$ $\Rightarrow \vec{AB} + \vec{DC} = 2 \vec{E F}$ => D đúng.

Đề kiểm tra Giữa kì 2 Toán 11 có đáp án (Mới nhất)

Đề kiểm tra Giữa kì 2 Toán 11 có đáp án (Mới nhất) (Đề 3)

Danh sách câu hỏi

Bài thi liên quan

Có thể bạn quan tâm

Các bài thi hot trong chương