Câu hỏi:
03/04/2024 40
Cho tứ diện ABCD. Gọi G là trọng tâm tam giác BCD. Hai điểm M, N lần lượt thuộc BC, CD sao cho . Chứng minh rằng
bốn điểm A, M, N, G đồng phẳng.
Cho tứ diện ABCD. Gọi G là trọng tâm tam giác BCD. Hai điểm M, N lần lượt thuộc BC, CD sao cho . Chứng minh rằng
bốn điểm A, M, N, G đồng phẳng.
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
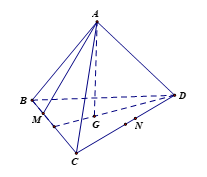
Ta có: (1).
(2).
Cộng vế với vế của (1) với (2), ta được:
(3)
Vì G trọng tâm nên (4).
Thay (3) vào (4) được: , từ hệ thức này chứng tỏ ba véc tơ đồng phẳng. Suy ra bốn điểm A, M, N, G đồng phẳng.
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 2:
Cho hàm số: , tìm khẳng định đúng trong các khẳng định sau:
I. f(x) liên tục tại x=3.
II. f(x) gián đoạn tại x=3.
III. f(x) liên tục trên R.
Cho hàm số: , tìm khẳng định đúng trong các khẳng định sau:
I. f(x) liên tục tại x=3.
II. f(x) gián đoạn tại x=3.
III. f(x) liên tục trên R.
Xem đáp án »
03/04/2024
98
Câu 3:
Cho tứ diện ABCD. Gọi I , J lần lượt là trung điểm của các cạnh AB và CD , G là trung điểm của đoạn thẳng IJ. Trong các đẳng thức sau, đẳng thức nào đúng?
Xem đáp án »
03/04/2024
74
Câu 4:
Cho hình chóp S.ABC có , . Tính góc giữa hai đường thẳng AB và SC.
Xem đáp án »
03/04/2024
69
Câu 6:
Trong các mệnh đề sau, mệnh đề nào sai? (Với giả thiết các đoạn thẳng và đường thẳng không song song hoặc trùng với phương chiếu).
Trong các mệnh đề sau, mệnh đề nào sai? (Với giả thiết các đoạn thẳng và đường thẳng không song song hoặc trùng với phương chiếu).
Xem đáp án »
03/04/2024
57


