Giải Toán 10 Bài 3: Tích của một số với một vectơ
1. Tích của một số với một vectơ và các tính chất
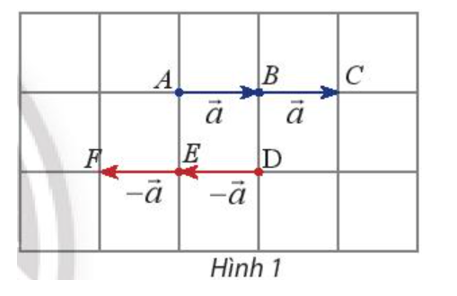
Lời giải:
Vectơ →a+→a có hướng từ A sang C.
Vectơ (−→a)+(−→a) có hướng từ D sang F.
Thực hành 1 trang 95 Toán lớp 10 Tập 1: Cho hai vectơ →a,→b và một điểm M như Hình 3.
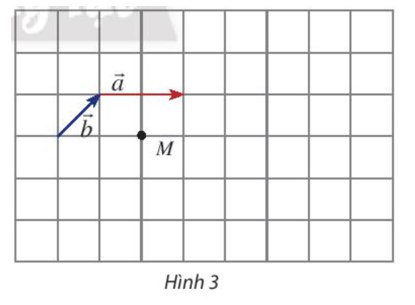
a) Hãy vẽ các vectơ →MN=3→a, →MP=−3→b .
b) Cho biết mỗi ô vuông có cạnh bằng 1. Tính: |3→b|, |−3→b|, |2→a+2→b|.
Lời giải:
a) Ta thấy 3 > 0 nên hai vectơ →MN và →a cùng hướng.
Do đó từ M kẻ đường thẳng d song song với đường thẳng a.
Trên đường thẳng d, về bên phải điểm M chọn điểm N sao cho MN = 6.
Khi đó →MN=3→a.
Do -3 < 0 nên hai vectơ →MP và →b ngược hướng.
Do đó từ M kẻ đường thẳng c song song với đường thẳng b.
Trên đường thẳng c, về bên trái điểm M chọn P sao cho MP = 3.
Khi đó →MP=−3→b.
Ta có hình vẽ như sau:
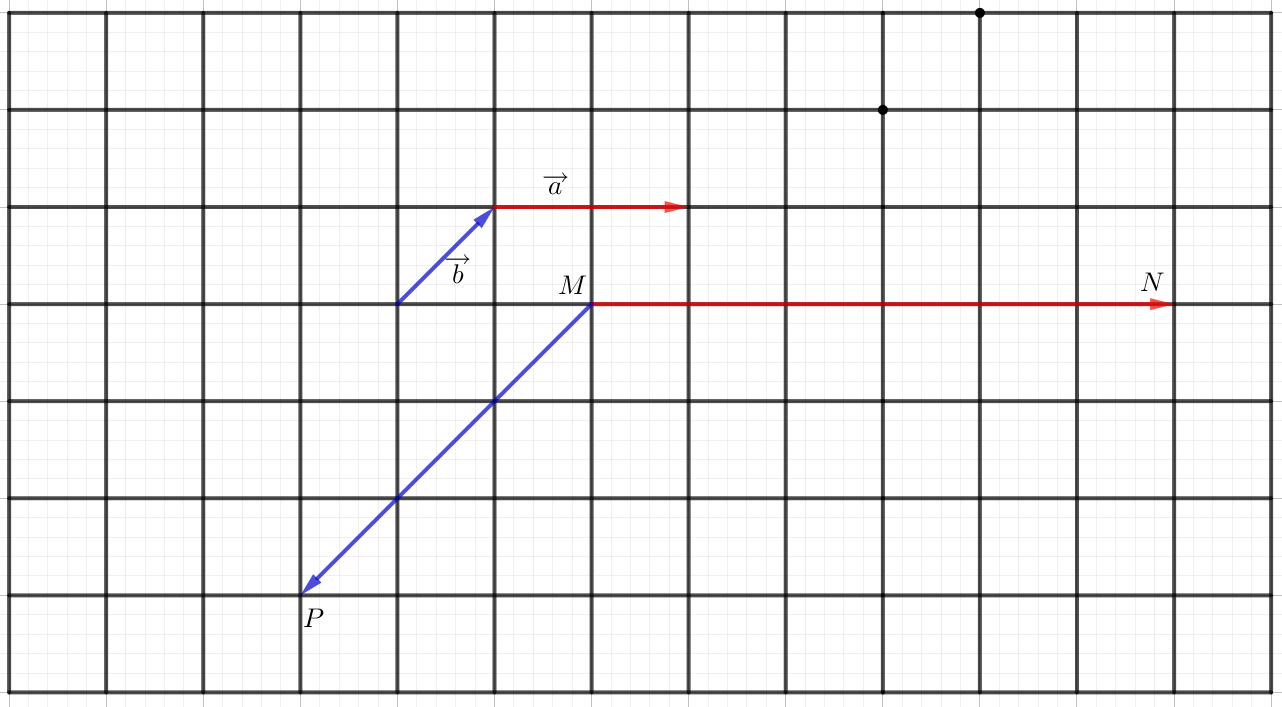
b) Ta thấy MP là độ dài cạnh huyền của 1 tam giác vuông cân có cạnh bằng 3.
Do đó MP = √32+32=3√2.
Ta thấy 3→b và −3→b là hai vectơ đối nên |3→b|=|−3→b|=|→MP|=3√2.
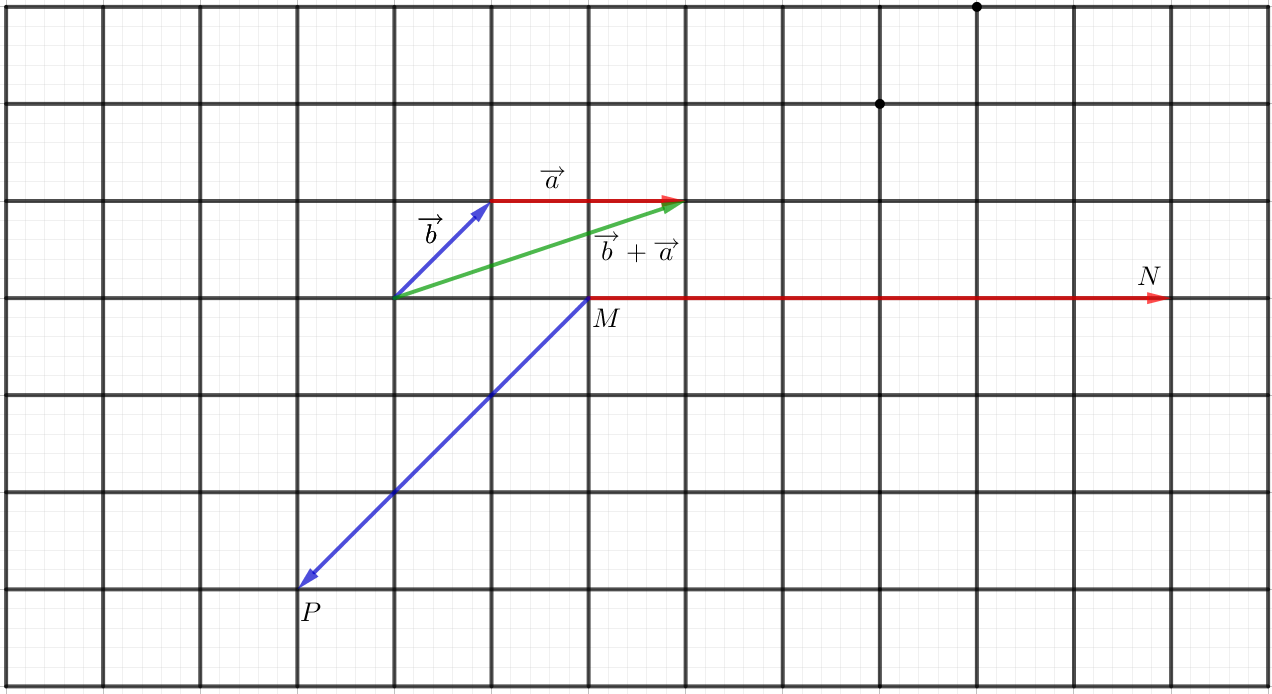
Ta thấy |→b+→a| là độ cạnh huyền của 1 tam giác vuông có độ dài 2 cạnh góc vuông lần lượt là 1 và 3.
Khi đó |→b+→a|=√32+12=√10.
Do đó |2→b+2→a|=|2→a+2→b|=2√10.
Vậy |3→b|=|−3→b|=3√2; |2→a+2→b|=2√10.
Lời giải:
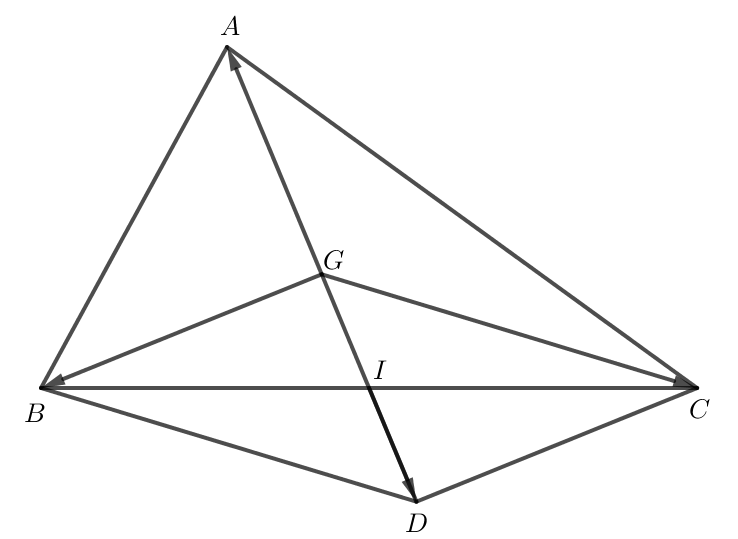
Phần thuận: G là trọng tâm của tam giác ABC thì →MA+→MB+→MC=3→MG.
Chứng minh:
Do G là trọng tâm của tam giác ABC nên →GA+→GB+→GC=→0.
Do đó →MG+→GA+→MG+→GB+→MG+→GC=3→MG hay →MA+→MB+→MC=3→MG.
Phần đảo: Tam giác ABC có →MA+→MB+→MC=3→MG thì G là trọng tâm của tam giác ABC.
Chứng minh:
→MA+→MB+→MC=3→MG
⇒→MG+→GA+→MG+→GB+→MG+→GC=3→MG
⇒→GA+→GB+→GC=→0
Dựng hình bình hành GBDC và gọi I là giao điểm của GD và BC.
Áp dụng quy tắc hình bình hành ta có →GB+→GC=→GD.
Mà →GA+→GB+→GC=→0 hay →GA+→GD=→0.
Do đó →GA=−→GD.
Khi đó |→GA|=|−→GD| hay GA = GD.
Hình bình hành GBDC có I là giao điểm hai đường chéo GD và BC nên I là trung điểm của BC và I là trung điểm của GD.
Do I là trung điểm của GD nên GI = 12GD = 12GA.
GI = 12GA nên AI = GI + GA = 12GA + GA = 32GA hay AG = 23AI.
Tam giác ABC có AI là đường trung tuyến, lại có AG = 23AI nên G là trọng tâm của tam giác ABC.
Vậy ta có điều phải chứng minh.
Lời giải:
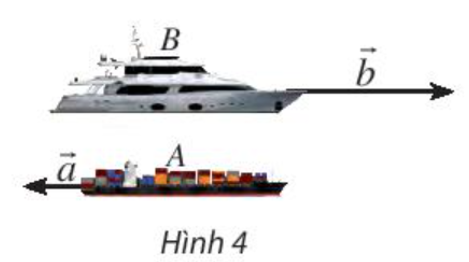
Ta thấy hai vectơ →a và →b ngược hướng và |→b|=50; |→a|=20.
⇒|→b|=52|→a|.
Vậy →b=−52→a.
2. Điều kiện để hai vectơ cùng phương
Lời giải:
Ta thấy với →b khác →0 thì |→a||→b| ≥ 0.
Do đó hai vectơ →c và →b là hai vectơ cùng hướng.
Mà →a và →b là hai vectơ cùng phương nên hai vectơ →a và →c cùng hướng khi hai vectơ →a và →b cùng hướng; hai vectơ →a và →c ngược hướng khi hai vectơ →a và →b ngược hướng.
Do →c=|→a||→b|.→b nên |→c|=||→a||→b|.→b|=|→a||→b|.|→b|=|→a|.
Do đó độ dài của hai vectơ →a và →c bằng nhau.
Lời giải:
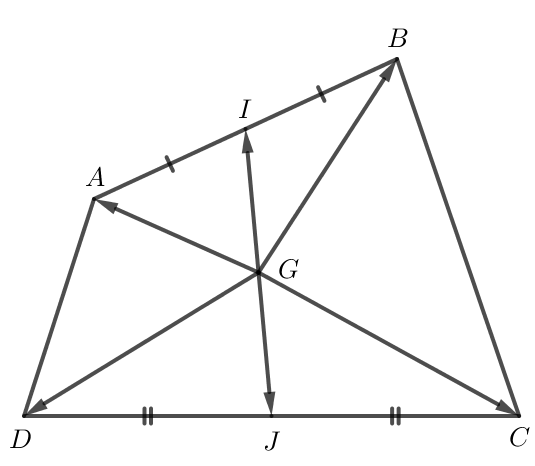
Do I là trung điểm của AB nên →GA+→GB=2→GI.
Do J là trung điểm của CD nên →GC+→GD=2→GJ.
Do đó →GA+→GB+→GC+→GD=2→GI+2→GJ hay →GI+→GJ=→0.
Do →GI+→GJ=→0 nên G là trung điểm của IJ.
Vậy I, G, J thẳng hàng.
Bài tập
a) →MA+→MB+→MC+→MD=4→MO;
b) →AB+→AC+→AD=2→AC.
Lời giải:
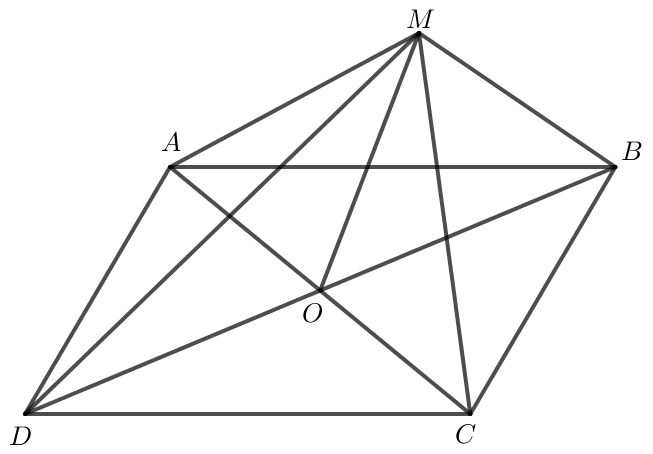
a) Hình bình hành ABCD có O là giao điểm hai đường chéo nên OA = OC, OB = OD.
Khi đó →OA và →OC là hai vectơ đối, →OB và →OD là hai vectơ đối.
Do đó →OA+→OB+→OC+→OD=→0.
Ta có
→MA+→MB+→MC+→MD=→MO+→OA+→MO+→OB+→MO+→OC+→MO+→OD
=4→MO+(→OA+→OB+→OC+→OD)
=4→MO
Vậy →MA+→MB+→MC+→MD=4→MO.
b) Áp dụng quy tắc hình bình hành ta có →AB+→AD=→AC.
Do đó →AB+→AD+→AC=→AC+→AC hay →AB+→AC+→AD=2→AC.
Vậy →AB+→AC+→AD=2→AC.
a) →AC+→BD=2→MN;
b) →AC+→BD=→BC+→AD.
Lời giải:
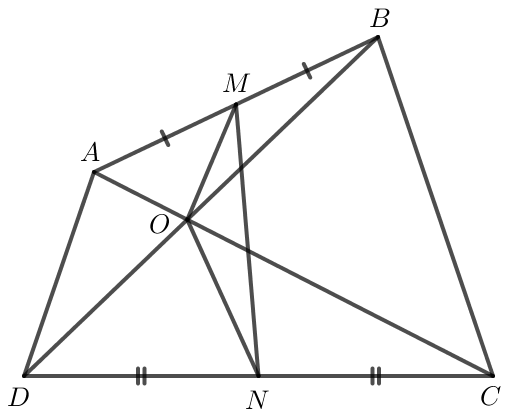
a) Gọi O là giao điểm hai đường chéo của tứ giác ABCD.
Do M là trung điểm của AB nên →OA+→OB=2→OM.
Do đó →AO+→BO=2→MO.
Do N là trung điểm của CD nên →OC+→OD=2→ON.
Do đó →AO+→BO+→OC+→OD=2→MO+2→ON.
hay →AO+→OC+→BO+→OD=2→MN.
Do đó →AC+→BD=2→MN.
b) Ta có →AD=→AC+→CD
Do đó
→BC+→AD=→BC+→AC+→CD=→AC+(→BC+→CD)=→AC+→BD.
Vậy →AC+→BD=→BC+→AD.
Lời giải:
Do →MA+4→MB=→0 nên →MA=−4→MB do đó |→MA|=|−4||→MB|=4|→MB| hay MA = 4MB.
Ta thấy -4 < 0 nên hai vectơ →MA và →MB ngược hướng.
Do đó A và B nằm ở hai phía so với điểm M.
Ta thực hiện vẽ như sau:
Bước 1. Vẽ đường thẳng d, trên đường thẳng d xác định hai điểm M và B.
Bước 2. Trên đường thẳng d, xác định điểm A sao cho A và B nằm ở hai phía so với điểm M thỏa mãn MA = 4MB.
Ta có hình vẽ như sau:

Lời giải:
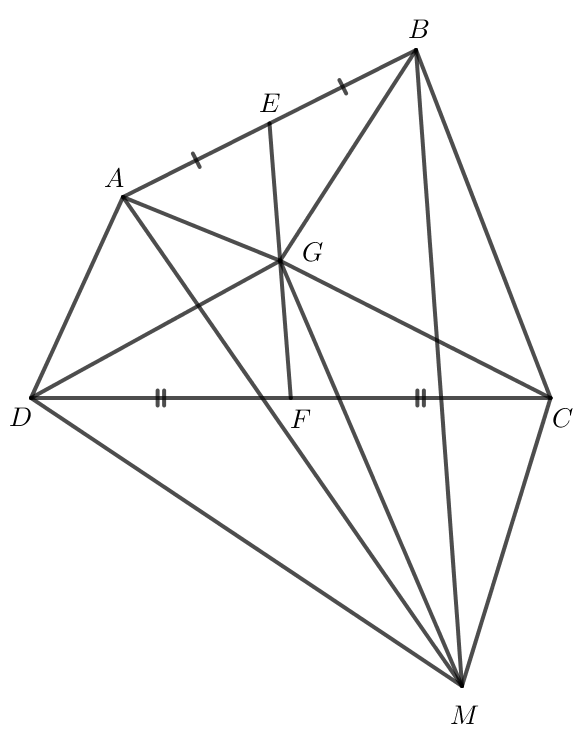
Do E là trung điểm của AB nên →GA+→GB=2→GE.
Do F là trung điểm của CD nên →GC+→GD=2→GF.
Do G là trung điểm của EF nên →GE+→GF=→0.
Do đó →GA+→GB+→GC+→GD=2→GE+2→GF=2(→GE+→GF)=→0.
Ta có
→MA+→MB+→MC+→MD=→MG+→GA+→MG+→GB+→MG+→GC+→MG+→GD
=4→MG+(→GA+→GB+→GC+→GD)
=4→MG
Vậy →MA+→MB+→MC+→MD=4→MG.
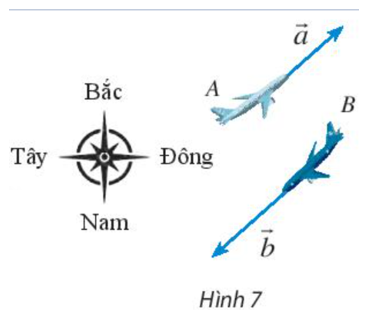
Lời giải:
Ta thấy hai vectơ →a và →b ngược hướng và |→a| = 600, |→b| = 800.
Do đó |→b|=800600|→a|=43|→a| hay b = 43a.
Mà hai vectơ →a và →b ngược hướng nên →b=−43→a.
Vậy →b=−43→a.
Bài 6 trang 97 Toán lớp 10 Tập 1: Cho hai điểm phân biệt A và B.
a) Xác định điểm O sao cho →OA+3→OB=→0.
b) Chứng minh rằng với mọi điểm M, ta có →MA+3→MB=4→MO.
Lời giải:
a) Do →OA+3→OB=→0 nên →OA=−3→OB do đó |→OA|=|−3||→OB|=3|→OB| hay OA = 3OB.
Ta thấy -3 < 0 nên hai vectơ →OA và →OB ngược hướng.
Do đó A và B nằm ở hai phía so với điểm O.
Ta thực hiện vẽ như sau:
Bước 1. Vẽ đường thẳng d, trên đường thẳng d xác định hai điểm O và B.
Bước 2. Trên đường thẳng d, xác định điểm A sao cho A và B nằm ở hai phía so với điểm O thỏa mãn OA = 3OB.
Ta có hình vẽ như sau:

b)
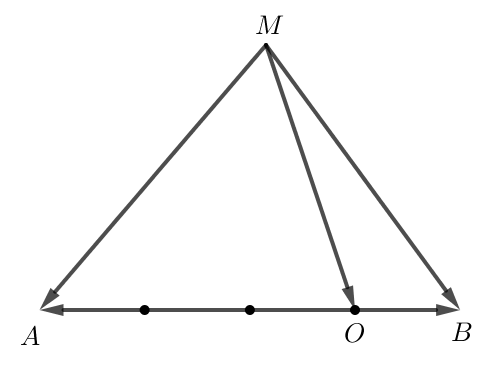
Ta có
→MA+3→MB=→MO+→OA+3(→MO+→OB)=4→MO+→OA+3→OB=4→MO.
Vậy →MA+3→MB=4→MO.
Bài 7 trang 97 Toán lớp 10 Tập 1: Cho tam giác ABC.
a) Xác định các điểm M, N, P thỏa mãn: →MB=12→BC, →AN=3→NB, →CP=→PA.
b) Biểu thị mỗi vectơ →MN, →MP theo hai vectơ →BC, →BA.
c) Chứng minh ba điểm M, N, P thẳng hàng.
Lời giải:
a) Do →MB=12→BC nên hai vectơ →MB và →BC cùng hướng.
Do đó M và C nằm ở hai phía so với điểm B sao cho MB = 12BC.
Do →AN=3→NB nên →AN+→NB=4→NB hay →AB=4→NB.
Do đó A và N nằm cùng phía so với điểm B sao cho NB = 14AB.
Do →CP=→PA nên →CP+→PA=2→PA hay →CA=2→PA.
Do đó P và C nằm cùng phía so với điểm A sao cho PA = 12CA.
Ta có hình vẽ sau:
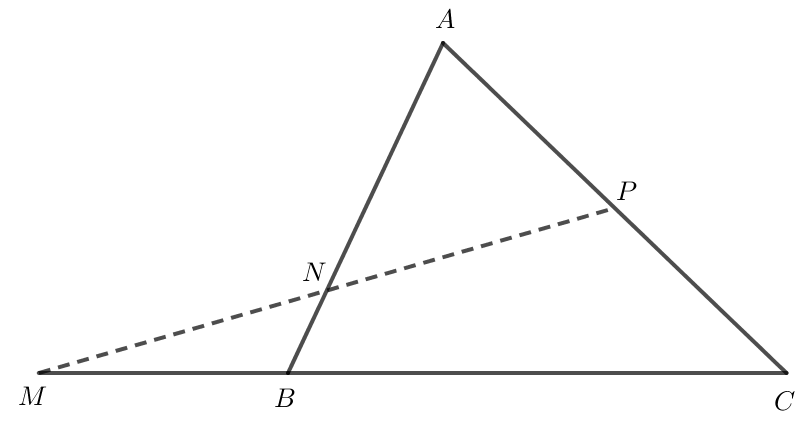
b) Ta có →MN=→BN−→BM.
Do →AN=3→NB nên →NA=3→BN⇒→BN+→NA=4→BN hay →BA=4→BN.
Do đó →BN=14→BA.
Do →MB=12→BC nên →BM=−12→BC.
Do đó →MN=→BN−→BM=14→BA+12→BC.
Ta có →MP=→BP−→BM.
Do đó P và C nằm cùng phía so với điểm A và PA = 12CA nên P là trung điểm của CA.
Do đó →BA+→BC=2→BP⇒→BP=12(→BA+→BC).
Do đó →MP=→BP−→BM=12(→BA+→BC)+12→BC=12→BA+→BC.
Ta thấy →MN=14→BA+12→BC; →MP=12→BA+→BC nên →MP=2→MN.
Do đó M, N, P thẳng hàng và N là trung điểm của MP.
Xem thêm lời giải bài tập SGK Toán lớp 10 Chân trời sáng tạo hay, chi tiết khác:
Bài 2: Tổng và hiệu của hai vectơ




