Cho hình bình hành ABCD có O là giao điểm hai đường chéo. Với M là điểm tùy ý, chứng minh rằng

Bài 1 trang 97 Toán lớp 10 Tập 1: Cho hình bình hành ABCD có O là giao điểm hai đường chéo. Với M là điểm tùy ý, chứng minh rằng:

a) $\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}+\overrightarrow{MD}=4\overrightarrow{MO}$;

b) $\overrightarrow{AB}+\overrightarrow{AC}+\overrightarrow{AD}=2\overrightarrow{AC}$.

Trả lời

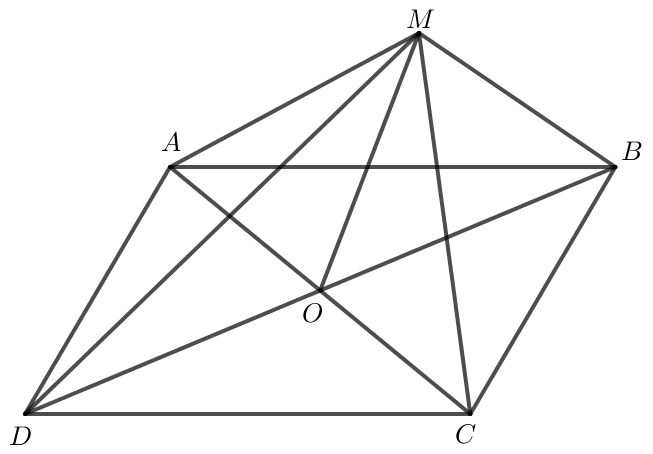
a) Hình bình hành ABCD có O là giao điểm hai đường chéo nên OA = OC, OB = OD.

Khi đó $\overrightarrow{OA}$ và $\overrightarrow{OC}$ là hai vectơ đối, $\overrightarrow{OB}$ và $\overrightarrow{OD}$ là hai vectơ đối.

Do đó $\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}+\overrightarrow{OD}=\overrightarrow{0}$.

Ta có

$$\begin{gathered} \overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}+\overrightarrow{M\text{D}} \\ =\overrightarrow{MO}+\overrightarrow{OA}+\overrightarrow{MO}+\overrightarrow{OB}+\overrightarrow{MO}+\overrightarrow{OC}+\overrightarrow{MO}+\overrightarrow{OD} \end{gathered}$$

$=4\overrightarrow{MO}+\left(\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}+\overrightarrow{OD}\right)$

$=4\overrightarrow{MO}$

Vậy $\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}+\overrightarrow{M\text{D}}=4\overrightarrow{MO}$.

b) Áp dụng quy tắc hình bình hành ta có $\overrightarrow{AB}+\overrightarrow{A\text{D}}=\overrightarrow{AC}$.

Do đó $\overrightarrow{AB}+\overrightarrow{A\text{D}}+\overrightarrow{AC}=\overrightarrow{AC}+\overrightarrow{AC}$ hay $\overrightarrow{AB}+\overrightarrow{AC}+\overrightarrow{A\text{D}}=2\overrightarrow{AC}$.

Vậy $\overrightarrow{AB}+\overrightarrow{AC}+\overrightarrow{A\text{D}}=2\overrightarrow{AC}$.

Xem thêm lời giải bài tập SGK Toán lớp 10 Chân trời sáng tạo hay, chi tiết khác:

Bài 1: Khái niệm vectơ

Bài 2: Tổng và hiệu của hai vectơ

Bài 3: Tích của một số với một vectơ

Bài 4: Tích vô hướng của hai vectơ

Bài tập cuối chương 5

Bài 1: Số gần đúng và sai số