Cho tam giác ABC. Chứng minh G là trọng tâm của tam giác ABC khi và chỉ khi vectơ MA + vectơ MB + vectơ MC = 3(vectơ MG)

Thực hành 2 trang 95 Toán lớp 10 Tập 1: Cho tam giác ABC. Chứng minh G là trọng tâm của tam giác ABC khi và chỉ khi $\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}=3\overrightarrow{MG}$.

Trả lời

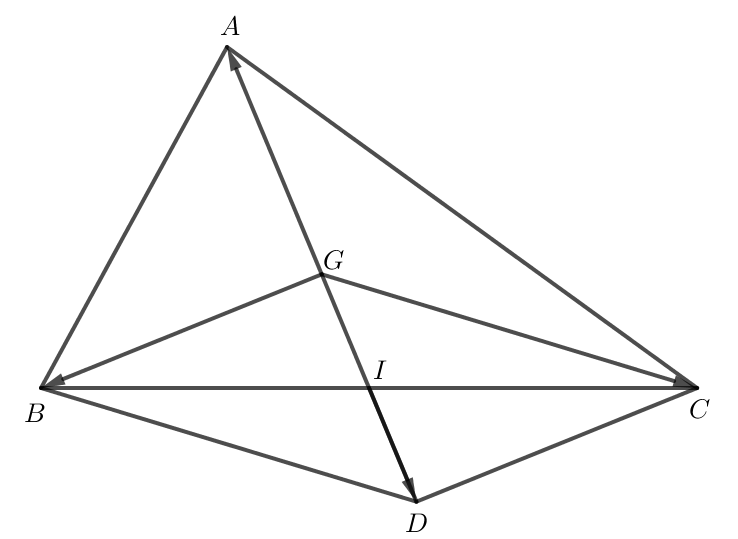
Phần thuận: G là trọng tâm của tam giác ABC thì $\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}=3\overrightarrow{MG}$.

Chứng minh:

Do G là trọng tâm của tam giác ABC nên $\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}=\overrightarrow{0}$.

Do đó $\overrightarrow{MG}+\overrightarrow{GA}+\overrightarrow{MG}+\overrightarrow{GB}+\overrightarrow{MG}+\overrightarrow{GC}=3\overrightarrow{MG}$ hay $\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}=3\overrightarrow{MG}$.

Phần đảo: Tam giác ABC có $\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}=3\overrightarrow{MG}$ thì G là trọng tâm của tam giác ABC.

Chứng minh:

$\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}=3\overrightarrow{MG}$

$\Rightarrow \overrightarrow{MG}+\overrightarrow{GA}+\overrightarrow{MG}+\overrightarrow{GB}+\overrightarrow{MG}+\overrightarrow{GC}=3\overrightarrow{MG}$

$\Rightarrow \overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}=\overrightarrow{0}$

Dựng hình bình hành GBDC và gọi I là giao điểm của GD và BC.

Áp dụng quy tắc hình bình hành ta có $\overrightarrow{GB}+\overrightarrow{GC}=\overrightarrow{G\text{D}}$.

Mà $\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}=\overrightarrow{0}$ hay $\overrightarrow{GA}+\overrightarrow{GD}=\overrightarrow{0}$.

Do đó $\overrightarrow{GA}=-\overrightarrow{GD}$.

Khi đó $\left|\overrightarrow{GA}\right|=\left|-\overrightarrow{G\text{D}}\right|$ hay GA = GD.

Hình bình hành GBDC có I là giao điểm hai đường chéo GD và BC nên I là trung điểm của BC và I là trung điểm của GD.

Do I là trung điểm của GD nên GI = $\frac{1}{2}$GD = $\frac{1}{2}$GA.

GI = $\frac{1}{2}$GA nên AI = GI + GA = $\frac{1}{2}$GA + GA = $\frac{3}{2}$GA hay AG = $\frac{2}{3}$AI.

Tam giác ABC có AI là đường trung tuyến, lại có AG = $\frac{2}{3}$AI nên G là trọng tâm của tam giác ABC.

Vậy ta có điều phải chứng minh.

Xem thêm lời giải bài tập SGK Toán lớp 10 Chân trời sáng tạo hay, chi tiết khác:

Bài 1: Khái niệm vectơ

Bài 2: Tổng và hiệu của hai vectơ

Bài 3: Tích của một số với một vectơ

Bài 4: Tích vô hướng của hai vectơ

Bài tập cuối chương 5

Bài 1: Số gần đúng và sai số