Câu hỏi:
03/04/2024 59
Cho hình lăng trụ tam giác ABC.A’B’C’.
a) Gọi E, F lần lượt là tâm của các mặt bên ABB’A’ và ACC’A’. Chứng minh đường
thẳng EF song song mặt phẳng (BCC’B’).
b) Gọi G là trọng tâm của tam giác ABC và H là trung điểm của B’C’. Chứng minh đường thẳng C’G song song với mặt phẳng (A’BH).
Cho hình lăng trụ tam giác ABC.A’B’C’.
a) Gọi E, F lần lượt là tâm của các mặt bên ABB’A’ và ACC’A’. Chứng minh đường
thẳng EF song song mặt phẳng (BCC’B’).
b) Gọi G là trọng tâm của tam giác ABC và H là trung điểm của B’C’. Chứng minh đường thẳng C’G song song với mặt phẳng (A’BH).
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
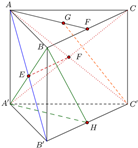
a) Ta có: E, F lần lượt là tâm của các hình bình hành ABB’A’ và ACC’A’.
Nên E và F lần lượt là trung điểm của các cạnh AB’ và AC’.
Xét ∆AB’C’ có E, F lần lượt là trung điểm của các cạnh AB’ và AC’.
Từ đó ta có EF là đường trung bình của ∆AB’C’.
Suy ra EF // B’C’.
Từ đó đường thẳng EF song song mặt phẳng (BCC’B’) .
b) Lấy F là trung điểm của BC .
Ta có AF // A’H Þ AF // (A’BH)
Và C’F // BH Þ C’F // (A’BH)
Suy ra (C’FA) // (A’BH).
Mà C’G Î (C’FA) Þ C’G // (A’BH).

a) Ta có: E, F lần lượt là tâm của các hình bình hành ABB’A’ và ACC’A’.
Nên E và F lần lượt là trung điểm của các cạnh AB’ và AC’.
Xét ∆AB’C’ có E, F lần lượt là trung điểm của các cạnh AB’ và AC’.
Từ đó ta có EF là đường trung bình của ∆AB’C’.
Suy ra EF // B’C’.
Từ đó đường thẳng EF song song mặt phẳng (BCC’B’) .
b) Lấy F là trung điểm của BC .
Ta có AF // A’H Þ AF // (A’BH)
Và C’F // BH Þ C’F // (A’BH)
Suy ra (C’FA) // (A’BH).
Mà C’G Î (C’FA) Þ C’G // (A’BH).
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Cho cấp số cộng (un). Công thức nào sau đây dùng để tính tổng n số hạng đầu của cấp số cộng đã cho?
Câu 2:
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M là điểm thuộc cạnh BC và (a) là mặt phẳng đi qua điểm M và song song với mặt phẳng (SAB). Thiết diện của hình chóp S.ABCD cắt bởi mặt phẳng (a) là một:
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M là điểm thuộc cạnh BC và (a) là mặt phẳng đi qua điểm M và song song với mặt phẳng (SAB). Thiết diện của hình chóp S.ABCD cắt bởi mặt phẳng (a) là một:
Câu 3:
Cho cấp số nhân (un) có dạng liệt kê là 3; 9; 27; 81;... Số hạng tổng quát của cấp số nhân đã cho là
Cho cấp số nhân (un) có dạng liệt kê là 3; 9; 27; 81;... Số hạng tổng quát của cấp số nhân đã cho là
Câu 6:
Cho cấp số cộng (un) có u7 = 27 và u20 = 79. Tổng 30 số hạng đầu của cấp số cộng này bằng
Cho cấp số cộng (un) có u7 = 27 và u20 = 79. Tổng 30 số hạng đầu của cấp số cộng này bằng
Câu 7:
Cho hình chóp S.ABCD, có đáy ABCD là hình bình hành tâm O. Gọi M, N lần lượt là trung điểm SA, SD. Mặt phẳng (OMN) song song với mặt phẳng nào sau đây?
Câu 8:
Cho (un) là cấp số cộng thoả mãn u3 + u5 + 2u9 = 100. Tính tổng 12 số hạng đầu của cấp số cộng.
Câu 13:
Cho cấp số nhân (un) có u1 = 5 và công bội q = 2. Tổng của bốn số hạng đầu của cấp số nhân bằng
Cho cấp số nhân (un) có u1 = 5 và công bội q = 2. Tổng của bốn số hạng đầu của cấp số nhân bằng
Câu 14:
Cho một đường thẳng a song song với mặt phẳng (P). Có bao nhiêu mặt phẳng chứa a và song song với (P)?
Cho một đường thẳng a song song với mặt phẳng (P). Có bao nhiêu mặt phẳng chứa a và song song với (P)?


