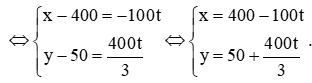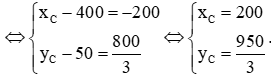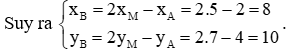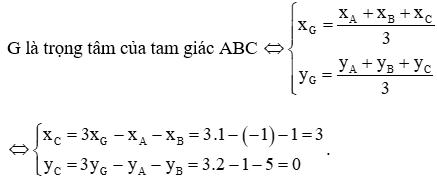Giải Toán 10 Bài 2: Biểu thức tọa độ của các phép toán vectơ
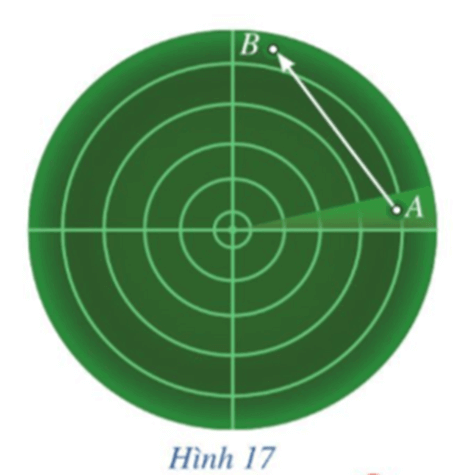
Làm thế nào để xác định được tọa độ của máy bay trực thăng tại thời điểm trên?
Lời giải:
Sau bài học này, ta giải quyết được bài toán này như sau:
Gọi T(x; y) là vị trí máy bay trực thăng tại thời điểm sau khi xuất phát t giờ (0 ≤ t ≤ 3).
Ta có: →AT=(x−400;y−50); →AB=(100−400;450−50)=(−300;400).
Theo bài ra có thời gian bay quãng đường AB là 3 giờ, suy ra tọa độ máy bay trực thăng tại thời điểm sau khi xuất phát t giờ chính là tại vị trí T sao cho →AT=t3→AB.
Ta có: t3→AB=t3(−300;400)=(t3.(−300);t3.400)=(−100t;400t3)
Khi đó: →AT=t3→AB⇔(x−400;y−50)=(−100t;400t3)
Vậy tọa độ của máy bay trực thăng tại thời điểm sau khi xuất phát t giờ là T(400−100t;50+400t3) với (0 ≤ t ≤ 3).
I. Biểu thức tọa độ của phép cộng hai vectơ, phép trừ hai vectơ, phép nhân một số với một vectơ
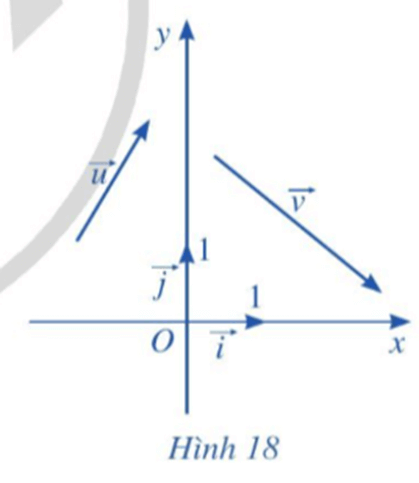
a) Biểu diễn các vectơ →u,→v theo hai vectơ →i và →j.
b) Biểu diễn các vectơ →u+→v,→u−→v,k→u (k ∈ ℝ) theo hai vectơ →i và →j.
c) Tìm tọa độ các vectơ →u+→v,→u−→v, k→u (k ∈ ℝ).
Lời giải:
a) Do →u=(x1;y1) và →v=(x2;y2) nên →u=x1→i+y1→j,→v=x2→i+y2→j.
b) Để biểu diễn vectơ →u+→v theo hai vectơ →i và →j, ta làm như sau:
Do →u=x1→i+y1→j,→v=x2→i+y2→j, vậy nên:
→u+→v=(x1→i+y1→j)+(x2→i+y2→j)=(x1→i+x2→i)+(y1→j+y2→j)=(x1+x2)→i+(y1+y2)→j
Tương tự, ta có:
→u−→v=(x1→i+y1→j)−(x2→i+y2→j)=(x1→i−x2→i)+(y1→j−y2→j)=(x1−x2)→i+(y1−y2)→j.
k→u=k(x1→i+y1→j)=kx1→i+ky1→j=(kx1)→i+(ky1)→j (k ∈ ℝ).
c) Do →u+→v=(x1+x2)→i+(y1+y2)→j nên tọa độ vectơ →u+→v là (x1 + x2; y1 + y2).
Do →u−→v=(x1−x2)→i+(y1−y2)→j nên tọa độ vectơ →u−→v là (x1 – x2; y1 – y2).
Do k→u=(kx1)→i+(ky1)→j nên tọa độ vectơ k→u là (kx1; ky1) với (k ∈ ℝ).
b) Cho →u=(√3;0),→v=(0;−√7). Tìm tọa độ của vectơ →w sao cho →w+→u=→v.
Lời giải:
a) Ta có: →u+→v+→w = ((– 2) + 0 + (– 2); 0 + 6 + 3). Vậy →u+→v+→w = (– 4; 9).
b) Ta có: →w+→u=→v⇔→w=→v−→u⇔→w=(0−√3;(−√7)−0). Vậy →w=(−√3;−√7).
Lời giải:
Gọi C(xC; yC) là vị trí máy bay trực thăng tại thời điểm sau khi xuất phát 2 giờ.
Ta có: →AC=(xC−400;yC−50); →AB=(100−400;450−50)=(−300;400).
Theo bài ra có thời gian bay quãng đường AB là 3 giờ, suy ra tọa độ máy bay trực thăng tại thời điểm sau khi xuất phát 2 giờ chính là tại vị trí C sao cho →AC=23→AB.
Ta có: 23→AB=23(−300;400)=(23.(−300);23.400)=(−200;8003)
Khi đó: →AC=23→AB⇔(xC−400;yC−50)=(−200;8003)
Vậy tọa độ của máy bay trực thăng tại thời điểm sau khi xuất phát 2 giờ là C(200;9503).
II. Tọa độ trung điểm đoạn thẳng và tọa độ trọng tâm tam giác
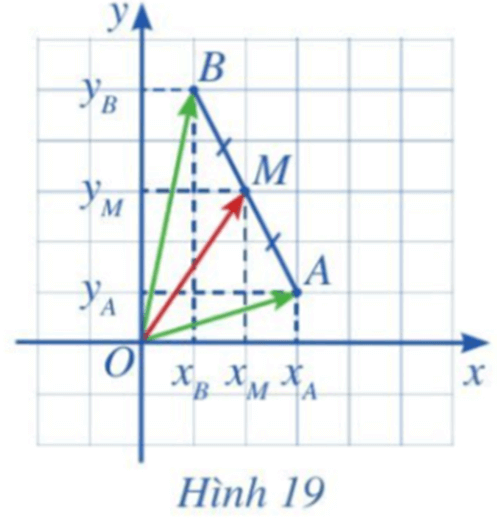
a) Biểu diễn vectơ →OM theo hai vectơ →OA và →OB.
b) Tìm tọa độ của M theo tọa độ của A và B.
Lời giải:
a) Vì M là trung điểm của AB nên với điểm O, ta có →OA+→OB=2→OM hay →OM=12(→OA+→OB)=12→OA+12→OB.
b) Tọa độ của vectơ →OA chính là tọa độ của điểm A(xA; yA) nên →OA=(xA;yA).
Tọa độ của vectơ →OB chính là tọa độ của điểm B(xB; yB) nên →OB=(xB;yB).
Ta có: 12→OA=12(xA;yA)=(12xA;12yA); 12→OB=12(xB;yB)=(12xB;12yB).
Do đó: →OM=12→OA+12→OB=(12xA+12xB;12yA+12yB).
Tọa độ của vectơ →OM chính là tọa độ của điểm M.
Vậy tọa độ của điểm M là M(xA+xB2;yA+yB2).
Lời giải:
Gọi tọa độ điểm B(xB; yB).
Vì M là trung điểm của AB nên xM=xA+xB2;yM=yA+yB2.
Vậy tọa độ điểm B là B(8; 10).
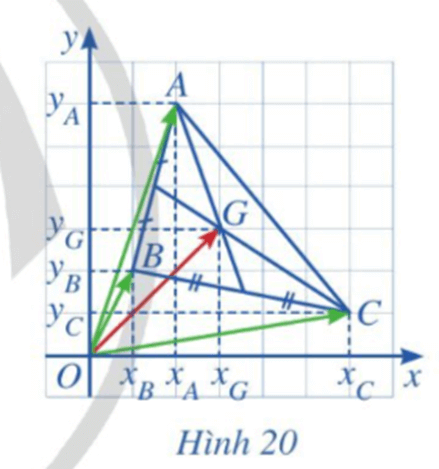
a) Biểu diễn vectơ →OG theo ba vectơ →OA,→OB và →OC.
b) Tìm tọa độ của G theo tọa độ của A, B, C.
Lời giải:
a) Vì G là trọng tâm của tam giác ABC nên với điểm O ta có →OA+→OB+→OC=3→OG hay →OG=13(→OA+→OB+→OC)=13→OA+13→OB+13→OC.
b) Tọa độ của vectơ →OA chính là tọa độ của điểm A(xA; yA) nên →OA=(xA;yA).
Tọa độ của vectơ →OB chính là tọa độ của điểm B(xB; yB) nên →OB=(xB;yB).
Tọa độ của vectơ →OC chính là tọa độ của điểm C(xC; yC) nên →OC=(xC;yC).
Ta có:; 13→OB=13(xB;yB)=(13xB;13yB), 13→OC=13(xC;yC)=(13xC;13yC)
Do đó: →OG=13→OA+13→OB+13→OC=(13xA+13xB+13xC;13yA+13yB+13yC).
Tọa độ của vectơ →OG chính là tọa độ của điểm G.
Vậy tọa độ của điểm G là G(xA+xB+xC3;yA+yB+yC3) .
Luyện tập 4 trang 69 Toán lớp 10 Tập 2: Cho ba điểm A(– 1; 1); B(1; 5); G(1; 2).
a) Chứng minh ba điểm A, B, G không thẳng hàng.
b) Tìm tọa độ điểm C sao cho G là trọng tâm của tam giác ABC.
Lời giải:
a) Ta có: →AB=(1−(−1);5−1)=(2;4), →AG=(1−(−1);2−1)=(2;1).
Vì 22≠41 nên →AB≠k→AG.
Vậy ba điểm A, B, G không thẳng hàng.
b) Gọi tọa độ điểm C(xC; yC).
Vậy tọa độ điểm C là C(3; 0).
III. Biểu thức tọa độ của tích vô hướng
a) Tính →i2;→j2;→i,→j.
b) Cho →u=(x1;y1),→v=(x2;y2). Tính tích vô hướng của →u.→v.
Lời giải:
a) Ta có: →i2=(→i)2=1;→j2=(→j)2=1;→i.→j=0 (vì , do hai trục tọa độ vuông góc với nhau).
b) Vì →u=(x1;y1),→v=(x2;y2).
Nên ta có: →u=x1→i+y1→j;→v=x2→i+y2→j.
Do đó →u.→v=(x1→i+y1→j).(→u=x2→i+y2→j)=x1x2.→i2+x1y2.(→i.→j)+y1x2.(→j.→i)+y1y2.→j2=x1x2+y1y2
(do →i2=(→i)2=1;→j2=(→j)2=1;→i.→j=→j.→i=0 )
Vậy →u.→v=x1x2+y1y2.
Bài tập
Bài 1 trang 72 Toán lớp 10 Tập 2: Trong mặt phẳng tọa độ Oxy, cho →a=(−1;2), →b=(3;1), →c=(2;−3).
a) Tìm tọa độ vectơ →u=2→a+→b−3→c.
b) Tìm tọa độ của vectơ →x sao cho →x+2→b=→a+→c.
Lời giải:
a) Ta có: 2→a=2(−1; 2)=(−2; 4), −3→c=−3(2; −3)=(−6; 9).
Khi đó →u=2→a+→b−3→c=2→a+→b+(−3→c)
=((−2)+3+(−6);4+1+9)=(−5; 14).
Vậy →u=(−5; 14).
b) Ta có: →x+2→b=→a+→c⇔→x=→a+→c−2→b
Có −2→b=−2(3; 1)= (−6; −2).
Do đó: →x=→a+→c−2→b=→a+→c+(−2→b)
=((−1)+2+(−6); 2+(−3)+(−2))=(−5; −3).
Vậy →x=(−5; −3).
Bài 2 trang 72 Toán 10 Tập 2: Trong mặt phẳng tọa độ Oxy, cho A(– 2; 3) ; B(4; 5); C(2; – 3).
a) Chứng minh ba điểm A, B, C không thẳng hàng.
b) Tìm tọa độ trọng tâm G của tam giác ABC.
c) Giải tam giác ABC (làm tròn các kết quả đến hàng đơn vị).
Lời giải
a) Ta có: →AB=(4−(−2); 5−3), do đó →AB=(6; 2).
→AC=(2−(−2); (−3)−3), do đó →AC=(4; −6).
Vì 64≠−3−6 nên →AB≠k→AC.
Do đó, ba điểm A, B, C không thẳng hàng.
b) G là trọng tâm tam giác ABC nên tọa độ điểm G là
xG=xA+xB+xC3=(−2)+4+23=43,
yG=yA+yB+yC3=3+5+(−3)3=53.
Vậy trọng tâm G có tọa độ là (43; 53).
c) Ta có: →BC=(2−4; (−3)−5), do đó →BC=(−2; −8).
BC=|→BC|=√(−2)2+(−8)2=2√17≈8.
AB=|→AB|=√62+22=2√10≈6.
AC=|→AC|=√42+(−6)2=2√13≈7.
Ta có: cos^BAC=cos(→AB, →AC)=→AB.→AC|→AB|. |→AC|=6.4+2.(−6)2√10.2√13≈0,26.
Suy ra ^BAC=75°.
Áp dụng hệ quả của định lí côsin trong tam giác ABC, ta có:
cosB = .
Suy ra .
Theo định lí tổng ba góc trong tam giác ABC, ta có:
Suy ra .
a) Tìm tọa độ các điểm A, B, C.
b) Trọng tâm hai tam giác ABC và MNP có trùng nhau không? Vì sao?
Lời giải
a) Gọi tọa độ các điểm A(xA; yA), B(xB; yB), C(xC; yC).
M(2; 0) là trung điểm của BC nên (1)
N(4; 2) là trung điểm của cạnh AC nên (2)
P(1; 3) là trung điểm của cạnh AB nên (3)
Từ (2) và (3) suy ra: (4)
Từ (1) và (4) suy ra: .
Do đó tọa độ điểm C là (5; – 1).
Thay tọa độ điểm C vào (2) ta được: .
Do đó A(3; 5).
Thay tọa độ điểm C vào (1) ta được: .
Do đó B(– 1; 1).
Vậy tọa độ các điểm A, B, C là A(3; 5), B(– 1; 1), C(5; – 1).
b) Gọi G là trọng tâm của tam giác ABC, ta có tọa độ của G là
Do đó (1).
Gọi G' là trọng tâm của tam giác MNP, ta có tọa độ của G' là
Do đó (2).
Từ (1) và (2) suy ra G ≡ G'.
Vậy trọng tâm hai tam giác ABC và MNP trùng nhau.
a) Tính số đo góc ABC (làm tròn kết quả đến hàng đơn vị theo đơn vị độ).
b) Tính chu vi của tam giác ABC.
c) Tìm tọa độ điểm M trên đường thẳng BC sao cho diện tích của tam giác ABC bằng hai lần diện tích của tam giác ABM.
Lời giải
a) Ta có: , do đó .
Suy ra .
, do đó .
Suy ra .
Ta có: .
Do đó, .
b) Ta có: , do đó .
Suy ra .
Chu vi của tam giác ABC là:
BA + BC + AC = = .
c) Theo câu a ta có , do đó tam giác ABC là tam giác tù.
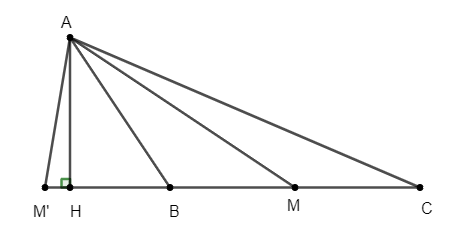
Dựng đường cao AH của tam giác ABC.
Do đó diện tích tam giác ABC là SABC = AH . BC. (1)
Vì M thuộc đường thẳng BC nên AH cũng là đường cao của tam giác ABM.
Do đó diện tích tam giác ABM là SABM = AH . BM. (2)
Vì diện tích của tam giác ABC bằng hai lần diện tích của tam giác ABM nên SABC = 2SABM. (3)
Từ (1), (2) và (3) suy ra AH . BC = 2 . AH . BM
⇔ BC = 2BM hay BM = BC.
Mà M thuộc đường thẳng BC.
Do đó M là trung điểm của BC hoặc M là điểm đối xứng với trung điểm của BC qua B.
Trường hợp 1: M là trung điểm của BC nên tọa độ của M là
Vậy .
Trường hợp 2: M là điểm đối xứng với trung điểm của BC qua B.
Suy ra điểm cần tìm là M', với B là trung điểm của MM' (M ở trường hợp 1).
Gọi tọa độ M'(xM'; yM').
Vì B là trung điểm của MM' nên
Suy ra .
Vậy .
Do đó có hai điểm M thỏa mãn yêu cầu bài toán.
Bài 5 trang 72 Toán 10 Tập 2: Cho ba điểm A(1; 1) ; B(4; 3) và C(6; – 2).
a) Chứng minh ba điểm A, B, C không thẳng hàng.
b) Tìm tọa độ điểm D sao cho tứ giác ABCD là hình thang có AB // CD và CD = 2AB.
Lời giải
a) Ta có: , do đó .
, do đó .
Vì nên .
Vậy ba điểm A, B, C không thẳng hàng.
b) Gọi tọa độ điểm D là (xD; yD).
Ta có: .
Do ABCD là hình thang có AB // CD nên hai vectơ cùng hướng và CD = 2AB nên suy ra .
Mà .
Khi đó .
Vậy tọa độ điểm D là (0; – 6).
Bài 6 trang 72 Toán 10 Tập 2: Chứng minh khẳng định sau:
Hai vectơ cùng phương khi và chỉ khi có một số thực k sao cho x1 = kx2 và y1 = ky2.
Lời giải
Hai vectơ và cùng phương khi và chỉ khi có số thực k sao cho .
Mà , suy ra .
Do đó .
Vậy hai vectơ cùng phương khi và chỉ khi có một số thực k sao cho x1 = kx2 và y1 = ky2.
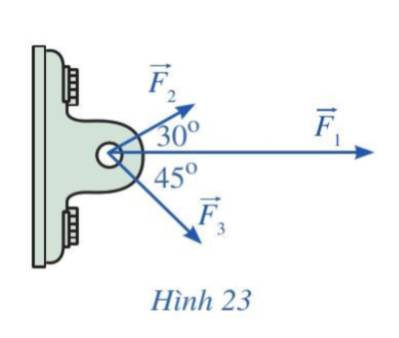
Lời giải
Dựng các hình bình hành như hình vẽ sau:
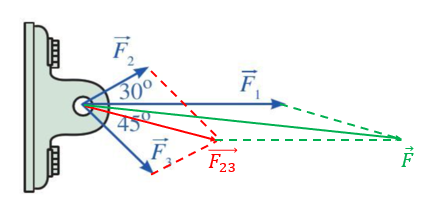
Theo quy tắc hình bình hành ta có: .
Lực tổng hợp tác động lên vật là với .
Ta có:
.
Áp dụng hệ quả của định lí côsin ta có:
Suy ra .
Mặt khác
Suy ra .
Ta lại có:
.
Vậy lực tổng hợp tác động lên vật có độ lớn là 2 598 N.
Xem thêm lời giải bài tập SGK Toán lớp 10 Cánh diều hay, chi tiết khác:
Chủ đề 2: Xây dựng mô hình hàm số bậc nhất, bậc hai biểu diễn số liệu dạng bảng
Bài 3: Phương trình đường thẳng
Bài 4: Vị trí tương đối và góc giữa hai đường thẳng. Khoảng cách từ một điểm đến một đường thẳng