Trong mặt phẳng tọa độ Oxy, cho tam giác ABC có A(2; 4); B(– 1; 1); C(– 8; 2). a) Tính số đo góc ABC (làm tròn kết quả đến hàng đơn vị theo đơn vị độ)

Bài 4 trang 72 Toán 10 Tập 2: Trong mặt phẳng tọa độ Oxy, cho tam giác ABC có A(2; 4); B(– 1; 1); C(– 8; 2).

a) Tính số đo góc ABC (làm tròn kết quả đến hàng đơn vị theo đơn vị độ).

b) Tính chu vi của tam giác ABC.

c) Tìm tọa độ điểm M trên đường thẳng BC sao cho diện tích của tam giác ABC bằng hai lần diện tích của tam giác ABM.

Trả lời

a) Ta có: $\overrightarrow{BA}=\left(2-\left(-1\right);4-1\right)$, do đó $\overrightarrow{BA}=\left(3;3\right)$.

Suy ra $BA=\left|\overrightarrow{BA}\right|=\sqrt{3^2+3^2}=3\sqrt{2}$.

$\overrightarrow{BC}=\left(\left(-8\right)-\left(-1\right);2-1\right)$,  do đó $\overrightarrow{BC}=\left(-7;1\right)$.

Suy ra $BC=\left|\overrightarrow{BC}\right|=\sqrt{{\left(-7\right)}^2+1^2}=5\sqrt{2}$.

Ta có: $\cos \widehat{ABC}=\cos \left(\overrightarrow{BA},\overrightarrow{BC}\right)=\frac{\overrightarrow{BA}.\overrightarrow{BC}}{\left|\overrightarrow{BA}\right|.\left|\overrightarrow{BC}\right|}$$=\frac{3.\left(-7\right)+3.1}{3\sqrt{2}.5\sqrt{2}}=-\frac{3}{5}$.

Do đó, $\widehat{ABC}=127°$.

b) Ta có: $\overrightarrow{AC}=\left(\left(-8\right)-2;2-4\right)$, do đó $\overrightarrow{AC}=\left(-10;-2\right)$.

Suy ra $AC=\left|\overrightarrow{AC}\right|=\sqrt{{\left(-10\right)}^2+{\left(-2\right)}^2}=2\sqrt{26}$.

Chu vi của tam giác ABC là:

BA + BC + AC = $3\sqrt{2}+5\sqrt{2}+2\sqrt{26}$= $8\sqrt{2}+2\sqrt{26}$.

c) Theo câu a ta có $\widehat{ABC}=127°$, do đó tam giác ABC là tam giác tù.

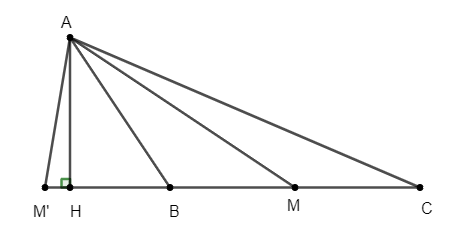
Dựng đường cao AH của tam giác ABC.

Do đó diện tích tam giác ABC là S_ABC = $\frac{1}{2}$AH . BC. (1)

Vì M thuộc đường thẳng BC nên AH cũng là đường cao của tam giác ABM.

Do đó diện tích tam giác ABM là S_ABM = $\frac{1}{2}$ AH . BM. (2)

Vì diện tích của tam giác ABC bằng hai lần diện tích của tam giác ABM nên S_ABC = 2S_ABM. (3)

Từ (1), (2) và (3) suy ra $\frac{1}{2}$AH . BC = 2 . $\frac{1}{2}$AH . BM

⇔ BC = 2BM hay BM = $\frac{1}{2}$BC.

Mà M thuộc đường thẳng BC.

Do đó M là trung điểm của BC hoặc M là điểm đối xứng với trung điểm của BC qua B.

Trường hợp 1: M là trung điểm của BC nên tọa độ của M là

 $\left\{\begin{array}{l}{x}_M=\frac{x_B+x_C}{2}=\frac{\left(-1\right)+\left(-8\right)}{2}=\frac{-9}{2}\\ y_M=\frac{y_B+y_C}{2}=\frac{1+2}{2}=\frac{3}{2}\end{array}\right.$

Vậy $M\left(\frac{-9}{2};\frac{3}{2}\right)$.

Trường hợp 2: M là điểm đối xứng với trung điểm của BC qua B.

Suy ra điểm cần tìm là M', với B là trung điểm của MM' (M ở trường hợp 1).

Gọi tọa độ M'(x_M'; y_M').

Vì B là trung điểm của MM' nên $\left\{\begin{array}{l}{x}_B=\frac{x_M+x_{M\text{'}}}{2}\\ y_B=\frac{y_M+y_{M\text{'}}}{2}\end{array}\right.$

Suy ra $\left\{\begin{array}{l}{x}_{M\text{'}}=2x_B-x_M=2.\left(-1\right)-\frac{-9}{2}=\frac{5}{2}\\ x_{M\text{'}}=2x_B-x_M=2.1-\frac{3}{2}=\frac{1}{2}\end{array}\right.$.

Vậy $M\text{'}\left(\frac{5}{2};\frac{1}{2}\right)$.

Do đó có hai điểm M thỏa mãn yêu cầu bài toán.

Xem thêm lời giải bài tập SGK Toán lớp 10 Cánh diều hay, chi tiết khác:

Chủ đề 2: Xây dựng mô hình hàm số bậc nhất, bậc hai biểu diễn số liệu dạng bảng

Bài 1: Tọa độ của vectơ

Bài 2: Biểu thức tọa độ của các phép toán vectơ

Bài 3: Phương trình đường thẳng

Bài 4: Vị trí tương đối và góc giữa hai đường thẳng. Khoảng cách từ một điểm đến một đường thẳng

Bài 5: Phương trình đường tròn