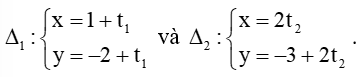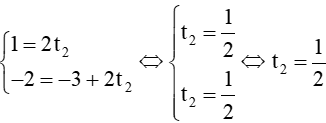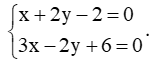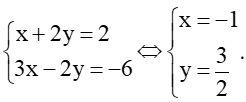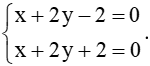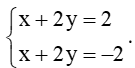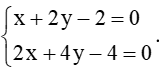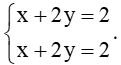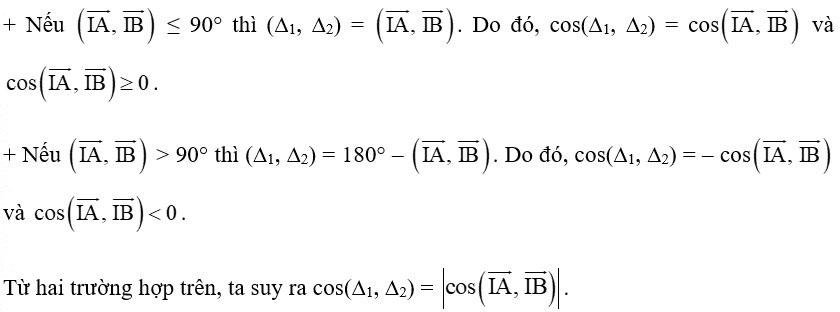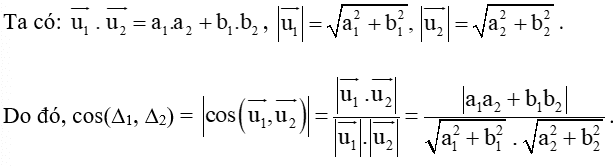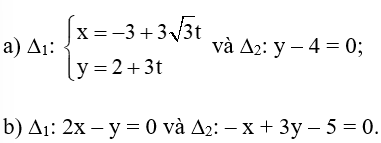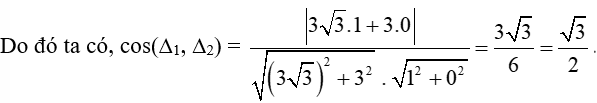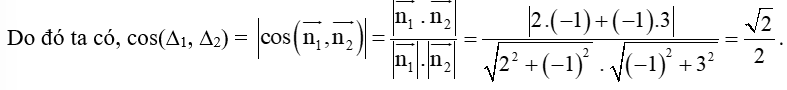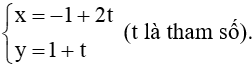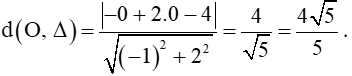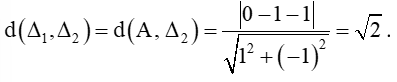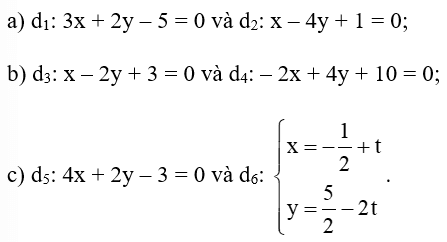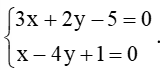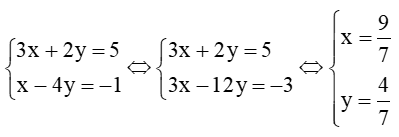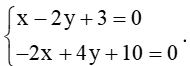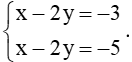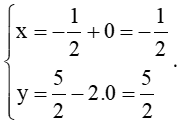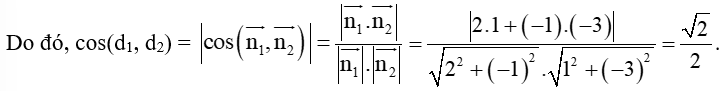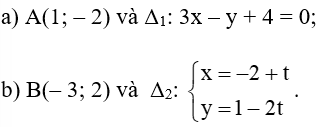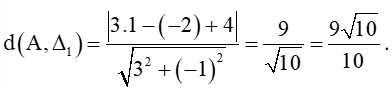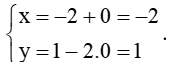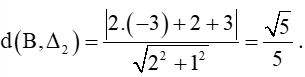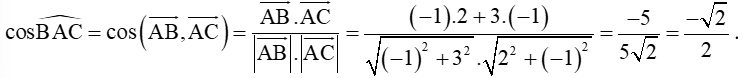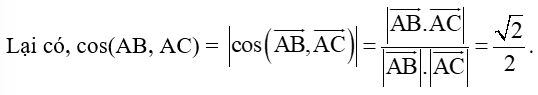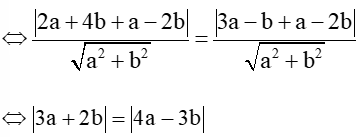Giải Toán 10 Bài 4: Vị trí tương đối và góc giữa hai đường thẳng. Khoảng cách từ một điểm đến một đường thẳng
Làm thế nào để xác định giao điểm M của hai đường thẳng a và b?
Lời giải:
Đầu tiên ta phải lập phương trình tổng quát của hai đường thẳng a và b, sau đó giải hệ hai phương trình trên, ta được nghiệm duy nhất chính là giao điểm của hai đường thẳng a và b.
I. Vị trí tương đối của hai đường thẳng
Hoạt động 1 trang 81 Toán lớp 10 Tập 2: Nêu vị trí tương đối của hai đường thẳng trong mặt phẳng.
Lời giải:
Có 3 vị trí tương đối của hai đường thẳng trong mặt phẳng, đó là cắt nhau, song song, trùng nhau.
a) ∆1 cắt ∆2;
b) ∆1 song song với ∆2;
c) ∆1 trùng với ∆2.
Lời giải:
Vì →u1 là vectơ chỉ phương của đường thẳng ∆1 nên giá của vectơ →u1 song song hoặc trùng với đường thẳng ∆1.
Vì →u2 là vectơ chỉ phương của đường thẳng ∆2 nên giá của vectơ →u2 song song hoặc trùng với đường thẳng ∆2.
a) ∆1 cắt ∆2
Khi đó giá của hai vectơ →u1,→u2 cắt nhau.
Do đó hai vectơ →u1,→u2 không cùng phương.
b) ∆1 song song với ∆2
Khi đó giá của hai vectơ →u1,→u2 song song hoặc trùng nhau.
Do đó hai vectơ →u1,→u2 cùng phương.
c) ∆1 trùng với ∆2
Khi đó giá của hai vectơ →u1,→u2 song song hoặc trùng nhau.
Do đó hai vectơ →u1,→u2 cùng phương.
Luyện tập 1 trang 82 Toán lớp 10 Tập 2: Xét vị trí tương đối của hai đường thẳng
Lời giải:
Đường thẳng ∆1 có vectơ chỉ phương là →u1=(1;1).
Đường thẳng ∆2 có vectơ chỉ phương là →u2=(2;2).
Ta có: →u2=2→u1, do đó →u1,→u2 cùng phương.
Chọn t1 = 0, ta có điểm M(1; – 2) thuộc ∆1. Thay tọa độ điểm M vào phương trình ∆2, ta được:
Vậy điểm M cũng thuộc ∆2.
Vậy hai đường thẳng ∆1 và ∆2 trùng nhau.
Δ1: 3x – 2y + 6 = 0;
Δ2: x + 2y + 2 = 0;
Δ3: 2x + 4y – 4 = 0.
Lời giải:
* Tọa độ giao điểm của đường thẳng d và đường thẳng ∆1 là nghiệm của hệ phương trình:
Phương trình trên tương đương với
Hệ có nghiệm duy nhất là (x; y) = (−1;32).
Do đó đường thẳng d cắt đường thẳng ∆1 tại điểm có tọa độ (−1;32).
* Tọa độ giao điểm của đường thẳng d và đường thẳng ∆2 là nghiệm của hệ phương trình:
Phương trình trên tương đương với
Hệ trên vô nghiệm.
Do đó đường thẳng d và đường thẳng ∆2 song song với nhau.
* Tọa độ giao điểm của đường thẳng d và đường thẳng ∆3 là nghiệm của hệ phương trình:
Phương trình trên tương đương với
Hệ trên có vô số nghiệm.
Do đó, hai đường thẳng d và ∆3 có vô số điểm chung nên d trùng với ∆3.
II. Góc giữa hai đường thẳng
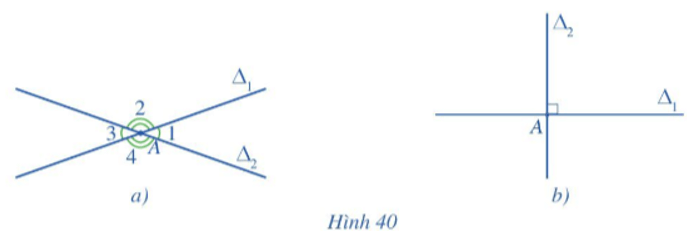
Quan sát Hình 40a và đọc tên một góc nhọn trong bốn góc đó.
Quan sát Hình 40b và nêu đặc điểm bốn góc tại đỉnh A.
Lời giải:
Quan sát Hình 40a, một góc nhọn trong bốn góc ở hình là góc A1 (có thể trả lời là góc A3).
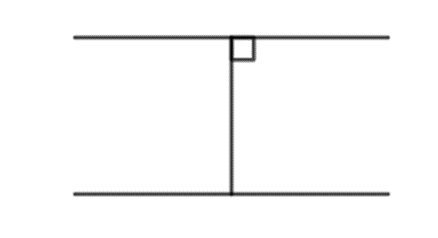
Quan sát Hình 40b, ta thấy bốn góc tại đỉnh A là bốn góc vuông, nên bốn góc này bằng nhau và bằng 90°.
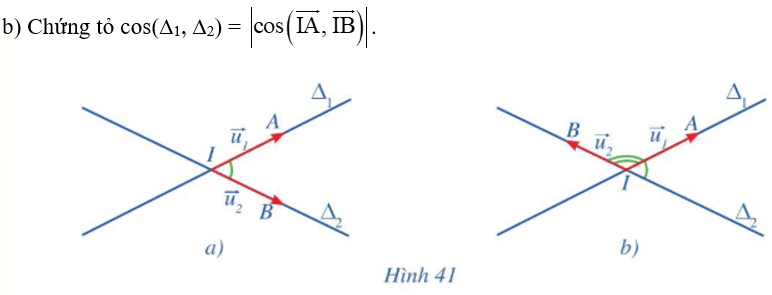
a) Quan sát Hình 41a, Hình 41b, hãy nhận xét về độ lớn của góc giữa hai đường thẳng ∆1, ∆2 và độ lớn của góc giữa hai vectơ →IA,→IB.
Lời giải:
a) Quan sát Hình 41a, ta thấy góc giữa hai vectơ →IA,→IB có độ lớn bằng góc giữa hai đường thẳng ∆1, ∆2.
Quan sát Hình 41b, ta thấy góc giữa hai vectơ →IA,→IB và góc giữa hai đường thẳng ∆1, ∆2 có tổng độ lớn bằng 180°.
b)
Lời giải:
Lời giải:
a) Đường thẳng ∆1 có vectơ chỉ phương là →u1=(3√3;3) .
Đường thẳng ∆2 có vectơ pháp tuyến là →n2=(0;1), do đó nó có một vectơ chỉ phương là →u2=(1;0).
Vậy (∆1, ∆2) = 30°.
b) Đường thẳng ∆1 có vectơ pháp tuyến là →n1=(2;−1).
Đường thẳng ∆2 có vectơ pháp tuyến là →n2=(−1;3).
Vậy (∆1, ∆2) = 45°.
III. Khoảng cách từ một điểm đến một đường thẳng
a) Tìm một vectơ chỉ phương của đường thẳng MH.
b) Viết phương trình tham số của đường thẳng MH.
c) Tìm tọa độ của H. Từ đó, tính độ dài đoạn thẳng MH.
Lời giải:
a) Đường thẳng ∆ có một vectơ pháp tuyến là →nΔ=(2;1).
Do H là hình chiếu của M lên đường thẳng ∆ nên MH ⊥ ∆.
Khi đó giá của vectơ pháp tuyến →nΔ=(2;1) song song hoặc trùng với đường thẳng MH.
Vậy một vectơ chỉ phương của đường thẳng MH là →uMH=→nΔ=(2;1).
b) Đường thẳng MH đi qua điểm M(– 1; 1) và có một vectơ chỉ phương là →uMH=(2;1) nên phương trình tham số của đường thẳng MH là
c) Điểm H thuộc đường thẳng MH nên gọi tọa độ H(– 1 + 2t; 1 + t).
Do H là hình chiếu của M lên ∆, do đó H cũng thuộc đường thẳng ∆ nên tọa độ điểm H thỏa mãn phương trình ∆, thay vào ta được:
2(– 1 + 2t) + (1 + t) – 4 = 0 ⇔ 5t – 5 = 0 ⇔ t = 1.
Do đó H(1; 2).
Vậy độ dài đoạn thẳng MH là MH = √(1−(−1))2+(2−1)2=√5.
b) Tính khoảng cách giữa hai đường thẳng song song ∆1: x – y + 1 = 0 và ∆2: x – y – 1 = 0.
Lời giải:
a) Ta có: x−4+y2=1⇔4(x−4+y2)=4⇔−x+2y−4=0.
Do đó, phương trình tổng quát của đường thẳng ∆: – x + 2y – 4 = 0.
Vậy khoảng cách từ O đến ∆ là
b) Khoảng cách giữa hai đường thẳng song song là khoảng cách từ 1 điểm thuộc đường thẳng này đến đường thẳng kia.
Cho x = 0, thay vào phương trình đường thẳng ∆1, ta được: 0 – y + 1 = 0 ⇔ y = 1.
Do đó, điểm A(0; 1) thuộc đường thẳng ∆1.
Vậy khoảng cách giữa hai đường thẳng song song ∆1 và ∆2 là:
Bài tập
Bài 1 trang 86 Toán lớp 10 Tập 2: Xét vị trí tương đối của mỗi cặp đường thẳng sau:
Lời giải:
a) Tọa độ giao điểm của đường thẳng d1 và d2 là nghiệm của hệ phương trình
Hệ trên tương đương với
Hệ có nghiệm duy nhất (x; y) = (97;47).
Vậy hai đường thẳng d1 và d2 có 1 điểm chung, tức là chúng cắt nhau tại giao điểm (97;47).
b) Tọa độ giao điểm của đường thẳng d3 và d4 là nghiệm của hệ phương trình
Hệ trên tương đương với
Do đó, hệ vô nghiệm.
Vậy hai đường thẳng d3 và d4 không có điểm chung, tức là d3 // d4.
c) Đường thẳng d5 có một vectơ pháp tuyến là →n5=(4;2), do đó nó có một vectơ chỉ phương là →u5=(2;−4).
Đường thẳng d6 có một vectơ chỉ phương là →u6=(1;−2).
Ta có: →u5=2→u6 nên hai vectơ →u5,→u6 cùng phương.
Ứng với t = 0, thay vào phương trình d6, ta được
Do đó, điểm M(−12;52) thuộc đường thẳng d6.
Thay tọa độ điểm M vào phương trình đường thẳng d5, ta được: 4.(−12)+2.52−3=0⇔ 0 = 0.
Khi đó điểm M thuộc đường thẳng d5.
Vậy hai đường thẳng d5 và d6 trùng nhau.
Lời giải:
Đường thẳng d1 có vectơ pháp tuyến là →n1=(2;−1).
Đường thẳng d2 có vectơ pháp tuyến là →n2=(1;−3).
Vậy (d1, d2) = 45°.
Lời giải:
a) Khoảng cách từ A đến ∆1 là:
b) Đường thẳng ∆2 có một vectơ chỉ phương là →u2=(1;−2), do đó nó có một vectơ pháp tuyến là →n2=(2;1).
Ứng với t = 0 thay vào phương trình ∆2 ta được:
Do đó điểm H(– 2; 1) thuộc ∆2.
Khi đó phương trình tổng quát của đường thẳng ∆2 là 2(x + 2) + 1(y – 1) = 0 hay 2x + y + 3 = 0.
Do đó, khoảng cách từ B đến ∆2 là:
Δ1: mx – y + 1 = 0 và Δ2: 2x – y + 3 = 0.
Lời giải:
Đường thẳng ∆1 có một vectơ pháp tuyến là →n1=(m;−1).
Đường thẳng ∆2 có một vectơ pháp tuyến là →n2=(2;−1).
Ta có: ∆1 ⊥ ∆2 ⇔ ⇔→n1⊥→n2⇔→n1.→n2=0⇔m . 2 + (– 1) . (– 1) = 0 ⇔ m = −12.
Vậy m = −12 thì hai đường thẳng ∆1 và ∆2 vuông góc với nhau.
Lời giải:
Ta có: →AB=(−1;3),→AC=(2;−1).
Do đó, ^BAC=135°.
Do đó, (AB, AC) = 45°.
Lời giải:
Gọi d là đường thẳng đi qua B và cách đều A và C.
Do d đi qua B(– 1; 2) nên phương trình đường thẳng d có dạng a(x + 1) + b(y – 2) = 0 hay ax + by + a – 2b = 0 (với a và b không đồng thời bằng 0).
Vì d cách đều A và C nên d(A, d) = d(C, d).
Trường hợp 1: 3a + 2b = 4a – 3b ⇔ a = 5b.
Chọn b = 1, a = 5 . 1 = 5, ta có phương trình đường thẳng d là 5x + y + 5 – 2 = 0 hay 5x + y + 3 = 0.
Trường hợp 2: 3a + 2b = – (4a – 3b) ⇔ 7a = b.
Chọn a = 1, b = 7 . 1 = 7, ta có phương trình đường thẳng d là x + 7y + 1 – 2 . 7 = 0 hay x + 7y – 13 = 0.
Vậy phương trình đường thẳng cần lập là 5x + y + 3 = 0 hoặc x + 7y – 13 = 0.
Lưu ý: Do vectơ là vectơ pháp tuyến của đường thẳng d, mà một đường thẳng có vô số vectơ pháp tuyến, nên khi ta có hệ thức liên hệ giữa a và b thì ta có thể chọn a rồi suy ra b hoặc ngược lại.
a) Tính côsin góc giữa hai đường đi của hai tàu A và B.
b) Sau bao lâu kể từ thời điểm xuất phát hai tàu gần nhau nhất?
c) Nếu tàu A đứng yên ở vị trí ban đầu, tàu B chạy thì khoảng cách ngắn nhất giữa hai tàu bằng bao nhiêu?
Lời giải
a) Giả sử đường đi của tàu A là đường thẳng ∆1, phương trình tham số của đường thẳng ∆1 là: . Đường thẳng ∆1 có vectơ chỉ phương là .
Đường đi của tàu B là ∆2, vị trí của tàu B có tọa độ là (4 – 30t; 3 – 40t), do đó phương trình tham số của đường thẳng ∆2: . Đường thẳng ∆2 có vectơ chỉ phương là .
Khi đó .
Vậy côsin góc giữa hai đường đi của hai tàu A và B là .
b) +) Ứng với t = 0, thay vào phương trình tham số của ∆1 ta có: .
Do đó điểm A(3; – 4) thuộc ∆1.
Đường thẳng ∆1 đi qua điểm A(3; – 4) và có một vectơ pháp tuyến là .
Vậy phương trình tổng quát của ∆1 là:
5(x – 3) + 7(y + 4) = 0 hay 5x + 7y + 13 = 0.
+) Ứng với t = 0, thay vào phương trình tham số của ∆2 ta có: .
Do đó điểm B(4; 3) thuộc ∆2.
Đường thẳng ∆2 đi qua điểm B(4; 3) và có một vectơ pháp tuyến là .
Vậy phương trình tổng quát của ∆2 là:
4(x – 4) – 3(y – 3) = 0 hay 4x – 3y – 7 = 0.
+) Tọa độ giao điểm của hai đường thẳng ∆1 và ∆2 là nghiệm của hệ phương trình:
.
Hệ trên có nghiệm duy nhất .
Suy ra hai đường thẳng ∆1 và ∆2 cắt nhau tại điểm có tọa độ .
Khi đó hai tàu A và tàu B gần nhau nhất khi hai tàu ở vị trí tọa độ .
Thay tọa độ vào phương trình tham số ∆1 ta được:
.
Vậy sau giờ kể từ thời điểm xuất phát thì hai tàu gần nhau nhất.
c) Tàu A đứng yên ở vị trí ban đầu nên tàu A đứng ở vị trí có tọa độ A(3; – 4) (ứng với t = 0).
Khoảng cách ngắn nhất giữa hai tàu là khoảng cách từ điểm A đến đường đi của tàu B (đường thẳng ∆2: 4x – 3y – 7 = 0).
Ta có: d(A, ∆2) = .
Vậy nếu tàu A đứng yên ở vị trí ban đầu, tàu B chạy thì khoảng cách ngắn nhất giữa hai tàu bằng 3,4 km.
Xem thêm lời giải bài tập SGK Toán lớp 10 Cánh diều hay, chi tiết khác:
Bài 2: Biểu thức tọa độ của các phép toán vectơ
Bài 3: Phương trình đường thẳng