Câu hỏi:
03/04/2024 37
Cho tứ diện ABCD với đáy BCD là tam giác vuông cân tại C. Các điểm M, N, P, Q lần lượt là trung điểm của AB, AC, BC, CD. Góc giữa MN và PQ bằng
Cho tứ diện ABCD với đáy BCD là tam giác vuông cân tại C. Các điểm M, N, P, Q lần lượt là trung điểm của AB, AC, BC, CD. Góc giữa MN và PQ bằng
A. 45°;
B. 60°;
C. 30°
D. 0°.
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
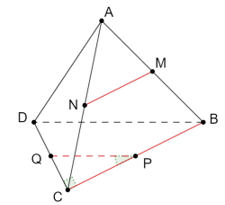
Vì M, N lần lượt là trung điểm của các cạnh AB, AC.
Nên MN là đường trung bình của tam giác ABC. Suy ra MN // BC.
Ta có MN // BC nên góc giữa MN và PQ là góc giữa BC và PQ.
Do đó góc giữa MN và PQ là .
Mà Q, P lần lượt là trung điểm của các cạnh CD, BC nên QP là đường trung bình của tam giác BCD.
Từ đó suy ra QP // BD nên góc (hai góc đồng vị và với tam giác
BCD vuông cân tại C).

Vì M, N lần lượt là trung điểm của các cạnh AB, AC.
Nên MN là đường trung bình của tam giác ABC. Suy ra MN // BC.
Ta có MN // BC nên góc giữa MN và PQ là góc giữa BC và PQ.
Do đó góc giữa MN và PQ là .
Mà Q, P lần lượt là trung điểm của các cạnh CD, BC nên QP là đường trung bình của tam giác BCD.
Từ đó suy ra QP // BD nên góc (hai góc đồng vị và với tam giác
BCD vuông cân tại C).
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Cho hình lập phương ABCD.A1B1C1D1. Góc giữa hai đường thẳng AC và DA1 bằng
Cho hình lập phương ABCD.A1B1C1D1. Góc giữa hai đường thẳng AC và DA1 bằng
Câu 2:
Hàm số y = f (x) có đồ thị như hình bên. Hàm số gián đoạn tại điểm có hoành độ bằng bao nhiêu?
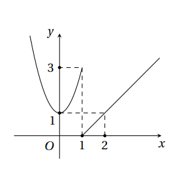
Hàm số y = f (x) có đồ thị như hình bên. Hàm số gián đoạn tại điểm có hoành độ bằng bao nhiêu?

Câu 3:
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, SA vuông góc với đáy và Số đo của góc giữa đường thẳng SC và mặt phẳng (ABCD) bằng
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, SA vuông góc với đáy và Số đo của góc giữa đường thẳng SC và mặt phẳng (ABCD) bằng
Câu 5:
Cho hình chóp S.ABCD có đáy là hình vuông và SA vuông góc với đáy. Khẳng định nào sau đây đúng?
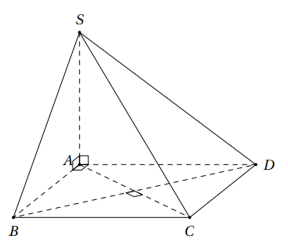
Cho hình chóp S.ABCD có đáy là hình vuông và SA vuông góc với đáy. Khẳng định nào sau đây đúng?

Câu 6:
Cho hình chóp S.ABC có SA ^ (ABC) và đáy là tam giác vuông tại A với AB = a, AC = 2a. Gọi a là góc giữa đường thẳng SA và mặt phẳng (SBC). Giá trị của tan a bằng
Cho hình chóp S.ABC có SA ^ (ABC) và đáy là tam giác vuông tại A với AB = a, AC = 2a. Gọi a là góc giữa đường thẳng SA và mặt phẳng (SBC). Giá trị của tan a bằng
Câu 8:
Cho tứ diện đều ABCD. Gọi M, N lần lượt là trung điểm các cạnh AB và BC. Tính số đo góc giữa hai đường thẳng MN và CD.
Cho tứ diện đều ABCD. Gọi M, N lần lượt là trung điểm các cạnh AB và BC. Tính số đo góc giữa hai đường thẳng MN và CD.
Câu 9:
Cho tứ diện ABCD có AB = CD = a. Gọi M và N lần lượt là trung điểm của AD và BC. Xác định độ dài đoạn thẳng MN để góc giữa hai đường thẳng AB và MN bằng 30°.
Cho tứ diện ABCD có AB = CD = a. Gọi M và N lần lượt là trung điểm của AD và BC. Xác định độ dài đoạn thẳng MN để góc giữa hai đường thẳng AB và MN bằng 30°.
Câu 10:
Cho hình lập phương ABCD.A’B’C’D’. Góc giữa hai đường thẳng BA’ và CD bằng
Cho hình lập phương ABCD.A’B’C’D’. Góc giữa hai đường thẳng BA’ và CD bằng


