43 câu hỏi trắc nghiệm thuộc Bộ 20 đề thi giữa học kì 1 Toán 11 năm 2022

Câu 1:

Tìm tập xác định D của hàm số $y = \tan x + \frac{1}{\sin x}$ .

A. $D = ℝ \ \{k π | k \in ℤ\}$ .

B.

$D = ℝ \ \{\frac{π}{2} + k π | k \in ℤ\}$ .

C.

$D = ℝ \ \{\frac{k π}{2} | k \in ℤ\}$ .

D.

$D = ℝ \ \{k 2 π | k \in ℤ\}$ .

Xem đáp án

Hàm số xác định $\Leftrightarrow \sin 2 x \neq 0 \Leftrightarrow x \neq \frac{k π}{2}, k \in ℤ$ .

$\Rightarrow$ Chọn đáp án C.

Câu 2:

Cho hàm số y = tan x. Khẳng định nào sau đây sai?

A. Hàm số là hàm số chẵn.

B. Hàm số tuần hoàn với chu kỳ

$π .$

C. Hàm số đồng biến trên mỗi khoảng

$(- \frac{π}{2} + k π; \frac{π}{2} + k π), k \in ℤ .$

D. Tập xác định của hàm số là

$ℝ \ \{\frac{π}{2} + k π, k \in ℤ\} .$

Xem đáp án

Hàm số y = tan x là hàm số lẻ

$\Rightarrow$ Chọn đáp án A.

Câu 3:

Cho hai đường thẳng cắt nhau d và d'. Có bao nhiêu phép tịnh tiến biến đường thẳng d thành đường thẳng d'?

A. Không có phép tịnh tiến nào.

B. Có một phép tịnh tiến duy nhất.

C. Chỉ có hai phép tịnh tiến.

D. Có vô số phép tịnh tiến.

Xem đáp án

Phép tịnh tiến biến đường thẳng thành đường thẳng song song hoặc trùng với nó

$\Rightarrow$ Với hai đường thẳng cắt nhau d và d', không có phép tịnh tiến nào biến đường

thẳng d thành đường thẳng d'

$\Rightarrow$ Chọn đáp án A.

Câu 4:

Tìm chu kì tuần hoàn T của hàm số

$y = \sin (x + \frac{π}{3}) .$

A.

$T = π$ .

B.

$T = \frac{π}{3}$ .

C.

$T = 2 π$ .

D.

$T = \frac{π}{2}$

Xem đáp án

Ghi nhớ rằng, chu kì tuần hoàn của hàm số y = sin (ax + b) hoặc $y = \cos (a x + b), (a; b \in ℝ, a \neq 0)$ là $T = \frac{2 π}{|a|}$ . Do đó, chu kì tuần hoàn của hàm số $y = \sin (x + \frac{π}{3})$ là $T = 2 π$

Chọn đáp án C.

Câu 5:

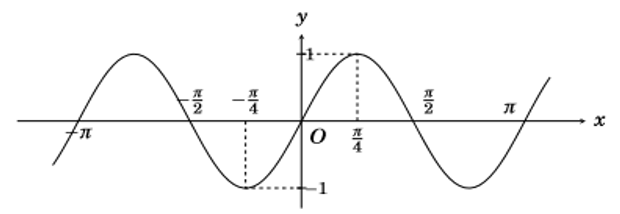
Cho hàm số $y = f (x) = \sin k x, k \in ℝ \ \{0\},$ có đồ thị như hình vẽ dưới đây:

$Cho hàm số y = f(x) = sin kx, k thuộc R\{0} có đồ thị như hình vẽ dưới đây: Xác định chu kì tuần hoàn T của hàm số này. (ảnh 1)$

Xác định chu kì tuần hoàn Tcủa hàm số này.

A.

$T = π$ .

B.

$T = 2 π$

C.

$T = \frac{π}{2}$ .

D.

$T = \frac{π}{4}$

Xem đáp án

Chọn đáp án A.

Câu 6:

Chọn khẳng định sai.

A. Phép tịnh tiến biến đường tròn thành đường tròn có cùng bán kính.

B. Phép vị tự biến đường thẳng thành đường thẳng song song hoặc trùng với nó.

C. Phép quay góc quay

$90^{0}$ biến đường thẳng thành đường thẳng song song hoặc trùng với nó.

D. Phép quay góc quay

$90^{0}$ biến đường thẳng thành đường vuông góc với nó.

Xem đáp án

Phép quay góc quay $90^{0}$ biến đường thẳng d thành đường thẳng d' tạo với d một góc $90^{0}$ .

Chọn đáp án C.

Câu 7:

Cho hàm số $y = \tan (x + \frac{π}{4}) .$ Tìm khẳng định đúng.

A. Hàm số đồng biến trên R.

B. Hàm số đồng biến trên

$(- \frac{π}{2}; \frac{π}{2})$ .

C. Hàm số đồng biến trên

$(- \frac{3 π}{4}; \frac{π}{4})$ .

D. Hàm số đồng biến trên

$(0; \frac{π}{2})$

Xem đáp án

Hàm số y = tan x đồng biến trên $(- \frac{π}{2}; \frac{π}{2})$ , hàm số $y = \tan (x + \frac{π}{4})$ đồng biến trên $(- \frac{π}{2} - \frac{π}{4}; \frac{π}{2} - \frac{π}{4})$ hay $(- \frac{3 π}{4}; \frac{π}{4})$ .

Chọn đáp án C.

Câu 8:

Cho hình vuông ABCD tâm O ,gọi M,N,P,Q lần lượt là trung điểm các cạnh $A B, B C, C D, D A .$ Phép dời hình nào sau đây biến $Δ A M O$ thành $Δ C P O$ ?

A. Phép tịnh tiến véc-tơ $\vec{A M}$

B. Phép tịnh tiến véc-tơ

$\vec{A O} .$

C. Phép quay tâm A góc quay

$180^{0}$

D. Phép quay tâm O góc quay

$- 180^{0}$ .

Xem đáp án

$Q_{(O, - 180^{0})} (A) = C; Q_{(O, - 180^{0})} (M) = P; Q_{(O, - 180^{0})} (O) = O$ .

$\Rightarrow Q_{(O, - 180^{0})}$ biến $Δ A M O$ thành $Δ C P O$ .

Chọn đáp án D.

Câu 9:

Tìm giá trị lớn nhất M của hàm số y = 3 - 2 sin 2x

A. M = 5

B. M = 3

C. M = 1

D. M = 6

Xem đáp án

Ta có $- 1 \leq \sin 2 x \leq 1 \Rightarrow - 2 \leq - 2 \sin 2 x \leq 2 \Rightarrow 1 \leq 3 - 2 \sin 2 x \leq 5$ .

Vậy M = 5.

Chọn đáp án A.

Câu 10:

Phương trình $4 \sin^{2} 2 x - 4 \cos 2 x - 1 = 0$ có nghiệm là

A. $x = \pm \frac{π}{6} + k π, k \in ℤ$ .

B.

$x = \pm \frac{π}{3} + k π, k \in ℤ$ .

C.

$x = \pm \frac{π}{6} + k 2 π, k \in ℤ$ .

D.

$x = \pm \frac{2 π}{3} + k π, k \in ℤ$ .

Xem đáp án

Phương trình đã cho tương đương với: $4 (1 - \cos^{2} 2 x) - 4 \cos 2 x - 1 = 0$

$\Leftrightarrow - 4 \cos^{2} 2 x - 4 \cos 2 x + 3 = 0 \Leftrightarrow [\begin{array}{l} \cos 2 x = - \frac{3}{2} (v n) \\ \cos 2 x = \frac{1}{2} \end{array} \Leftrightarrow x = \pm \frac{π}{6} + k π, k \in ℤ$ .

Chọn đáp án A.

Câu 11:

Phương trình $\sin x - \sqrt{3} \cos x = 1$ có nghiệm là

A. $x = - \frac{π}{2} + k 2 π, x = \frac{7 π}{6} + k 2 π, k \in ℤ .$ .

B.

$x = \frac{π}{2} + k 2 π, x = - \frac{7 π}{6} + k 2 π, k \in ℤ$ .

C.

$x = \frac{π}{2} + k π, x = \frac{7 π}{6} + k π, k \in ℤ$ .

D.

$x = \frac{π}{2} + k 2 π, x = \frac{7 π}{6} + k 2 π, k \in ℤ$ .

Xem đáp án

Phương trình tương đương với: $\frac{1}{2} \sin x - \frac{\sqrt{3}}{2} \cos x = \frac{1}{2} \Leftrightarrow \sin \frac{π}{6} \sin x - \cos \frac{π}{6} \cos x = \frac{1}{2}$

$\Leftrightarrow \cos x \cos \frac{π}{6} - \sin x \sin \frac{π}{6} = - \frac{1}{2} \Leftrightarrow \cos (x + \frac{π}{6}) = - \frac{1}{2} \Leftrightarrow x + \frac{π}{6} = \pm \frac{2 π}{3} + k 2 π$

$\Leftrightarrow [\begin{array}{l} x = \frac{π}{2} + k 2 π \\ x = \frac{- 5 π}{6} + k 2 π \end{array} \Leftrightarrow [\begin{array}{l} x = \frac{π}{2} + k 2 π \\ x = \frac{7 π}{6} + k 2 π \end{array}, k \in ℤ$ .

Chọn đáp án D.

Câu 12:

Cho điểm I thuộc đoạn thẳng AB và AB = 4AI. Chọn khẳng định đúng.

A. Phép vị tự tâm I tỉ số k = 3 biến điểm A thành điểm B.

B. Phép vị tự tâm I tỉ số k = -4 biến điểm A thành điểm B.

C. Phép vị tự tâm I tỉ số k = 4 biến điểm A thành điểm B.

D. Phép vị tự tâm I tỉ số k = - 3 biến điểm A thành điểm B.

Xem đáp án

Chọn đáp án D.

Câu 13:

Cho hàm số y = sin x trên đoạn $[- \frac{3 π}{2}; \frac{5 π}{2}]$ có đồ thị như hình vẽ dưới đây:

Tìm tất cả giá trị

$x \in [- \frac{3 π}{2}; \frac{5 π}{2}]$ để hàm số nhận giá trị âm.

A. $(- π; 0); (π; 2 π)$ .

B.

$(0; π)$ .

C.

$(π; 2 π)$ .

D.

$(\frac{3 π}{2}; 2 π)$ .

Xem đáp án

Trên các khoảng $(- π; 0); (π; 2 π)$ đồ thị hàm số nằm phía dưới trục hoành nên hàm số nhận giá trị âm.

Chọn đáp án A.

Câu 14:

Cho tam giác ABC có AB = AC và góc $\hat{A B C} = 60 °$ . Phép quay tâm I góc quay $α = 90 °$ biến A thành M, biến B thành N, biến C thành H. Khi đó tam giác MNH là:

A. Tam giác vuông.

B. Tam giác vuông cân.

C. Tam giác đều.

D. Tam giác không đều.

Xem đáp án

Chọn đáp án C.

Câu 15:

Số nghiệm thuộc $[0; 2 π)$ của phương trình $\sin x = \frac{1}{3}$ là

A. 2

B. 1

C. 3

D. 4

Xem đáp án

Trên $[0; 2 π)$ phương trình $\sin x = \frac{1}{3}$ có hai nghiệm phân biệt: $x = \arcsin \frac{1}{3}, x = π - \arcsin \frac{1}{3}$ .

Chọn đáp án A.

Câu 16:

Tìm giá trị nhỏ nhất m của hàm số $y = 3 \sin^{2} x - 2 \cos^{2} x$ .

A. m = -5

B. m = 1

C. m = 3

D. m = -2

Xem đáp án

Ta có $y = 3 \sin^{2} x - 2 \cos^{2} x = 3 \sin^{2} x - 2 (1 - \sin^{2} x) = 5 \sin^{2} x - 2$ .

Ta có: $0 \leq \sin^{2} x \leq 1 \Leftrightarrow - 2 \leq 5 \sin^{2} x - 2 \leq 3$ .

Tồn tại x để y = -2 nên m = -2.

Chọn đáp án D.

Câu 17:

Cho hình bình hành ABCD tâm O, phép quay $Q_{(O, - 180^{0})}$ biến đường thẳng AD thành đường thẳng

A. CD

B. CB

C. BA

D. AC

Xem đáp án

Chọn đáp án B.

Câu 18:

Tìm chu kỳ tuần hoàn T của hàm số $y = \sin^{2} x - 2 \cos^{2} x$ .

A. $T = 2 π$ .

B.

$T = π$

C.

$T = 4 π$

D.

$T = \frac{π}{2}$ .

Xem đáp án

Ta có $y = \sin^{2} x - 2 \cos^{2} x = 1 - 3 \cos^{2} x = - \frac{1}{2} - \frac{3}{2} \cos 2 x$ . Suy ra chu kỳ $T = \frac{2 π}{2} = π$ .

Chọn đáp án B.

Câu 19:

Cho phương trình $2 + 2 \sin 2 x + \sin x - \cos x = 0$ . Giải phương trình đã cho bằng cách đặt t = sin x - cos x, ta thu được phương trình nào sau đây?

A. $2 t^{2} + t = 0$ .

B.

$2 + 2 t^{2} + t = 0$ .

C.

$- 2 t^{2} + t + 4 = 0$ .

D.

$- 2 t^{2} + t + 2 = 0$ .

Xem đáp án

Đặt $t = \sin x - \cos x \Rightarrow t^{2} = 1 - \sin 2 x \Leftrightarrow \sin 2 x = 1 - t^{2}$ , thay vào PT đã cho ta được:

$2 + 2 (1 - t^{2}) + t = 0 \Leftrightarrow - 2 t^{2} + t + 4 = 0.$

Chọn đáp án C.

Câu 20:

Phép quay tâm O(0;0) góc quay $90^{0}$ biến điểm A(0;5) thành điểm A' có tọa độ là

A. (0;-5)

B. (-5;0)

C. (2;3)

D. (3;0)

Xem đáp án

Chọn đáp án B.

Câu 21:

Biểu diễn điểm ngọn của tất cả cung có số đo là nghiệm của phương trình $\cos 2 x = - \frac{1}{2}$ ta được

A. Hai điểm đối xứng với nhau qua trục hoành.

B. Bốn đỉnh của một hình vuông.

C. Tám đỉnh của một bát giác đều.

D. Bốn đỉnh của một hình chữ nhật mà không phải là hình vuông.

Xem đáp án

$\cos 2 x = - \frac{1}{2} \Leftrightarrow \cos 2 x = \cos \frac{2 π}{3} \Leftrightarrow [\begin{matrix} x = \frac{π}{3} + k π \\ x = - \frac{π}{3} + k π \end{matrix}$

Biểu diễn lên đường tròn lượng giác là được 4 đỉnh của một hình chữ nhật mà không phải là hình vuông.

Chọn đáp án D.

Câu 22:

Nghiệm âm lớn nhất của phương trình $\sin x - \cos x = \sqrt{2}$ là

A. $- \frac{π}{2}$ .

B.

$- \frac{5 π}{4}$ .

C.

$- \frac{π}{4}$ .

D.

$- \frac{3 π}{4}$ .

Xem đáp án

Xét phương trình: $\sin x - \cos x = \sqrt{2} \Leftrightarrow \sin (x - \frac{π}{4}) = 1 \Leftrightarrow x - \frac{π}{4} = \frac{π}{2} + k 2 π$ $\Leftrightarrow x = \frac{3 π}{4} + k 2 π$ , $k \in ℤ$ .

Suy ra nghiệm âm lớn nhất của phương trình là $x = - \frac{5 π}{4}, (k = - 1)$ .

Chọn đáp án B.

Câu 23:

Phép vị tự tâm I(1;2) tỉ số 3 biến điểm A( 4;1) thành điểm có tọa độ là:

A. (16;1)

B. (14;1)

C. (6;5)

D. (10;-1)

Xem đáp án

$V_{(I,3)} (A) = A' (x' y') \Rightarrow \vec{I A'} = 3 \vec{I A} \Leftrightarrow \{\begin{cases} x' - 1 = 3 (4 - 1) \\ y' - 2 = 3 (1 - 2) \end{cases} \Leftrightarrow \{\begin{cases} x' = 10 \\ y' = - 1 \end{cases} \Rightarrow A' (10; - 1)$ .

Chọn đáp án D.

Câu 24:

Trong các phương trình đã cho sau đây, phương trình nào vô nghiệm?

A. $\tan^{2} x - 1 = 0$ .

B.

$\tan^{2} x + 1 = 0$ .

C.

$3 \tan^{2} x - 1 = 0$ .

D.

$\tan^{2} x - 3 = 0$ .

Xem đáp án

$\tan^{2} x \geq 0 \Rightarrow \tan^{2} x + 1 \geq 1 > 0, \forall x \in ℝ$ . Vậy $\tan^{2} x + 1 = 0$ vô nghiệm.

Chọn đáp án B.

Câu 25:

Trong mặt phẳng với hệ tọa độ Oxy, cho đường tròn (C) có phương trình ${(x - 1)}^{2} + {(y - 2)}^{2} = 4$ . Hỏi phép vị tự tâm O tỉ số k = 2 biến (C) thành đường tròn nào sau đây?

A. ${(x - 4)}^{2} + {(y - 2)}^{2} = 4$ .

B.

${(x - 4)}^{2} + {(y - 2)}^{2} = 16$ .

C.

${(x + 2)}^{2} + {(y + 4)}^{2} = 16$ .

D.

${(x - 2)}^{2} + {(y - 4)}^{2} = 16$ .

Xem đáp án

Chọn đáp án D.

Câu 26:

Gọi $x_{0}$ là nghiệm dương nhỏ nhất của phương trình $2 \sin^{2} x + \sin x - 1 = 0 (1)$ . Khẳng định nào sau đây đúng?

A.

$x_{0} = [\frac{5 π}{6}; \frac{3 π}{2}]$ .

B.

$x_{0} = (\frac{π}{6}; \frac{5 π}{6})$ .

C.

$x_{0} = (0; \frac{π}{4})$ .

D.

$x_{0} = (\frac{π}{2}; π)$ .

Xem đáp án

Chọn đáp án C.

Câu 27:

Phương trình

$\sin^{2} x - \sin 2 x + 2 \cos^{2} x = 1$ tương đương với phương trình nào sau đây?

A. $- 2 \tan x + 1 = 0$ .

B.

$\cos x (1 - 2 \sin x) = 0$ .

C.

$\sin x (2 \sin x - 1) = 0$ .

D.

$\cos x (2 \sin x - \cos x) = 0$ .

Xem đáp án

Xét phương trình: $\sin^{2} x - \sin 2 x + 2 \cos^{2} x = 1 \Leftrightarrow - (1 - \sin^{2} x) - 2 \sin x . \cos x + 2 \cos^{2} x = 0$

$\Leftrightarrow \cos^{2} x - 2 \sin x . \cos x = 0 \Leftrightarrow \cos x (\cos x - 2 \sin x) = 0 \Leftrightarrow \cos x (2 \sin x - \cos x) = 0$ .

Chọn đáp án D.

Câu 28:

Tìm giá trị nhỏ nhất M của hàm số

$y = 3 \sin x - 4 \cos x + 3.$

A. M = -2

B. M = -10

C. M = 2

D. M = 6

Xem đáp án

Chọn đáp án A.

Câu 29:

Trong mặt phẳng với hệ tọa độ Oxy, cho đường thẳng d: 3x - y + 1 = 0, đường thẳng nào trong các đường thẳng có phương trình sau là ảnh của d qua phép quay tâm O(0;0) góc $90^{0}$ ?

A. x + y + 1 = 0

B. x + 3y + 1 = 0

C. 3x + y + 2 = 0

D. x - y + 2 = 0

Xem đáp án

$Q_{(O {,90}^{0})} (d) = d' \Rightarrow d' ⊥ d \Rightarrow d' : x + 3 y + c = 0$

$M (0; 1) \in d$ , $Q_{(O {,90}^{0})} (M) = M' \Rightarrow M' (- 1; 0) \in d' \Rightarrow - 1 + 3.0 + c = 0 \Leftrightarrow c = 1$ .

d': x +3y + 1 = 0.

Chọn đáp án B.

Câu 30:

Cho các hàm số $y = \cos 2 x - \tan^{2} x - 9$ $, y = c o t 3 x - 7 \sin 2 x, y = |\sin 3 x| + \cos x - 5, y = 2 \cos 3 x - 9 \tan x + 1$ . Có bao nhiêu hàm số chẵn trong các hàm số trên?

A. 3

B. 4

C. 2

D. 1

Xem đáp án

Chọn đáp án C.

Câu 31:

Giả sử đoạn $[m; M]$ là tập giá trị của hàm số $y = \frac{\sin x + \cos x - 1}{\cos x - \sin x + 2}$ . Tính $S = M^{2} + m^{2}$ .

A. S = 5

B. S = 4

C. S = 6

D. S = $\frac{11}{2}$

Xem đáp án

Chọn đáp án A.

Câu 32:

Trong mặt phẳng với hệ tọa độ Oxy, cho đường thẳng d: 2x + y - 3 = 0. Phép vị tự tâm O tỉ số 2 biến đường thẳng d thành đường nào trong các đường sau?

A. 2x + y + 3 = 0

B. 2x + y - 6 = 0

C. 4x + 2y - 3 = 0

D. 4x + 2y - 5 = 0

Xem đáp án

Chọn đáp án B.

Câu 33:

Phương trình $\sin^{3} x + \cos^{3} x = \sin x - 2 \cos^{2} x$ có bao nhiêu nghiệm thuộc khoảng $(0; 2 π)$ ?

A. 3

B. 2

C. 1

D. 0

Xem đáp án

Chọn đáp án B.

Câu 34:

Trong mặt phẳng với hệ tọa độ Oxy, cho ba điểm $A (1; 4), B (4; 0)$ và C(-2;-2). Phép tịnh tiến theo vectơ $\vec{B C}$ biến tam giác ABC thành tam giác A'B'C' có trực tâm là điểm nào sau đây?

A. (-4;1)

B. (-1;4)

C. (-4;-1)

D. (4;1)

Xem đáp án

Chọn đáp án C.

Câu 35:

Biết rằng điều kiện của tham số m để phương trình $3 \cos^{2} x + (3 m - 1) \sin x + m - 3 = 0$ có nghiệm trong khoảng $(0; π)$ là $m \in (a; b]$ . Tính giá trị của biểu thức $T = 2 a^{2} - 5 b$ .

A. 2

B. -5

C. 7

D. -3

Xem đáp án

$3 \cos^{2} x + (3 m - 1) \sin x + m - 3 = 0 \Leftrightarrow 3 \sin^{2} x - (3 m - 1) \sin x - m = 0 \Leftrightarrow [\begin{array}{l} \sin x = - \frac{1}{3} \\ \sin x = m \end{array}$ .

Với $x \in (0; π) \Rightarrow \sin x > 0$ . Do đó để phương trình có nghiệm trên $(0; π)$ thì $0 < m \leq 1$ .

Khi đó $a = 0, b = 1 \Rightarrow T = - 5$ .

Chọn đáp án B.

Câu 36:

Trong mặt phẳng với hệ tọa độ Oxy, cho đường tròn $(C) : {(x + 2)}^{2} + {(y - 1)}^{2} = 4$ và đường thẳng d: x - y + 2 = 0 cắt nhau tại hai điểm A và B, gọi M là trung điểm của AB. Phép vị tự tâm O tỉ số k = 3 biến điểm M thành điểm M' có tọa độ là

A.

$(\frac{9}{2}; - \frac{3}{2})$ .

B. (9;-3).

C. (-9;3).

D.

$(\frac{- 9}{2}; \frac{3}{2})$ .

Xem đáp án

Chọn đáp án D.

Câu 37:

Cho hình vuông ABCD có $A (1; 1), B (- 1; 1), C (- 1; - 1), D (1; - 1) .$ Phép quay tâm O góc quay bằng $\frac{π}{4}$ biến hình vuông ABCD thành hình vuông A'B'C'D'. Gọi S là diện tích phần hình vuông A'B'C'D' nằm ngoài hình vuông ABCD. Tính S.

A.

$\sqrt{2}$

B.

$12 - 8 \sqrt{2}$

C.

$6 - 4 \sqrt{2}$

D.1

Xem đáp án

Chọn đáp án B.

Câu 38:

Phương trình cos 2x + 13 cos x - 6 = 0 có bao nhiêu nghiệm trên khoảng

$(0; \frac{7 π}{2})$ ?

A. 1

B. 3

C. 2

D. 4

Xem đáp án

Chọn đáp án B.

Câu 39:

Cho tam giác ABC nội tiếp đường tròn (O) trong đó B và C cố định. Quỹ tích trọng tâm G của tam giác ABC là

A. ảnh của đường thẳng BC qua phép tịnh tiến.

B. ảnh của đường thẳng BC qua phép đối xứng trục.

C. ảnh của (O) qua một phép vị tự.

D. ảnh của (O) qua phép tịnh tiến.

Xem đáp án

Chọn đáp án C.

Câu 40:

Gọi a là nghiệm âm lớn nhất và b là nghiệm dương nhỏ nhất của phương trình

$\sin 4 x + \cos 5 x = 0$ . Tính S = a + b

A.

$S = \frac{π}{18}$

B.

$S = \frac{π}{9}$

C.

$S = \frac{- 4 π}{3}$

D.

$S = \frac{π}{3}$

Xem đáp án

Chọn đáp án B.

Câu 41:

Giải phương trình

a) $2 \cos^{2} x - 5 \cos x + 2 = 0$

Xem đáp án

a) Ta có: $2 \cos^{2} x - 5 \cos x + 2 = 0 \Leftrightarrow [\begin{array}{l} \cos x = 2 (V« nghiÖm) \\ \cos x = \frac{1}{2} \end{array}$ .

$\Leftrightarrow \cos x = \cos \frac{π}{3} \Leftrightarrow x = \pm \frac{π}{3} + k 2 π, k \in ℤ$ .

Vậy tập nghiệm của phương trình đã cho là $S = \{\pm \frac{π}{3} + k 2 π| k \in ℤ\} .$

Câu 42:

Giải phương trình

b) $[1 + \cos (x + \frac{π}{2})] . \tan^{2} x - \cos x = 1$

Xem đáp án

b) Điều kiện: $\cos x \neq 0 \Leftrightarrow x \neq \frac{π}{2} + k π, (k \in ℤ)$

Phương trình $\Leftrightarrow (1 - \sin x) . \frac{\sin^{2} x}{\cos^{2} x} = \cos x + 1 \Leftrightarrow (1 - \sin x) . \frac{(1 - \cos x) (1 + \cos x)}{(1 - \sin x) (1 + \sin x)} = \cos x + 1$

$\Leftrightarrow (1 + \cos x) (\frac{1 - \cos x}{1 + \sin x} - 1) = 0 \Leftrightarrow (1 + \cos x) (\frac{\cos x + \sin x}{1 + \sin x}) = 0 \Leftrightarrow [\begin{array}{l} \cos x = - 1 \\ \sin x = - \cos x \end{array}$

$\Leftrightarrow [\begin{array}{l} x = π + k 2 π \\ \tan x = - 1 \end{array} \Leftrightarrow [\begin{array}{l} x = π + k 2 π \\ x = - \frac{π}{4} + k π \end{array} (k \in ℤ)$ . (thỏa điều kiện)

Vậy tập nghiệm của phương trình đã cho là $S = \{π + k 2 π; - \frac{π}{4} + k π| k \in ℤ\} .$

Câu 43:

Trong mặt phẳng với hệ tọa độ Oxy cho đường thẳng $Δ$ có phương trình 2x - 3y + 7 = 0. Phép tịnh tiến theo vectơ $\vec{u} (5; - 3)$ biến đường thẳng $Δ$ thành đường thẳng $Δ'$ . Viết phương trình đường thẳng $Δ'$ .

Xem đáp án

Gọi $M^{'} (x^{'}; y^{'}) \in Δ^{'}$ là ảnh của $M (x; y) \in Δ$ qua phép tịnh tiến theo $\vec{u} (5; - 3)$ .

Ta có $\{\begin{cases} x^{'} = x + a \\ y^{'} = y + b \end{cases} \Leftrightarrow \{\begin{cases} x = x^{'} - a = x^{'} - 5 \\ y = y^{'} - b = y^{'} + 3 \end{cases}$ .

Thay vào $Δ$ , ta được $2 (x^{'} - 5) - 3 (y^{'} + 3) + 7 = 0 \Leftrightarrow 2 x^{'} - 3 y^{'} - 12 = 0$ .

Vậy $Δ^{'} : 2 x - 3 y - 12 = 0$ .

Bộ 20 đề thi giữa học kì 1 Toán 11 năm 2022 - 2023 có đáp án

Bộ 20 đề thi giữa học kì 1 Toán 11 năm 2022 - 2023 có đáp án (Đề 4)

Danh sách câu hỏi

Bài thi liên quan

Có thể bạn quan tâm

Các bài thi hot trong chương