39 câu hỏi trắc nghiệm thuộc Bộ 20 đề thi giữa học kì 1 Toán 11 năm 2022

Câu 1:

Tìm tập xác định D của hàm số y = tan x:

A. $D = ℝ \ \{\frac{π}{4} + k 2 π | k \in ℤ\}$ .

B.

D = ℝ \ \{\frac{π}{2} + k π | k \in ℤ\}

.

C.

D = ℝ \ \{\frac{π}{4} + k π | k \in ℤ\}

.

D.

D = ℝ \ \{\frac{π}{4} + k \frac{π}{2} | k \in ℤ\}

.

Xem đáp án

Chọn D

Hàm số xác định khi $\cos 2 x \neq 0 \Leftrightarrow 2 x \neq \frac{π}{2} + k π \Leftrightarrow x \neq \frac{π}{4} + k \frac{π}{2} (k \in ℤ)$ .

Tập xác định của hàm số là: $D = ℝ \ \{\frac{π}{4} + k \frac{π}{2} | k \in ℤ\}$ .

Câu 2:

Tập giá trị của hàm số y = sin 2x là:

A.

[- 2; 2]

.

B.

[0; 2]

.

C.

[- 1; 1]

.

D.

[0; 1]

.

Xem đáp án

Chọn C

Ta có $- 1 \leq \sin 2 x \leq 1$ , $\forall x \in ℝ$ .

Vậy tập giá trị của hàm số đã cho là $[- 1; 1]$ .

Câu 3:

Tìm chu kì T của hàm số

y = \sin (5 x - \frac{π}{4})

.

A. $T = \frac{2 π}{5}$ .

B.

T = \frac{5 π}{2}

.

C.

T = \frac{π}{2}

.

D.

T = \frac{π}{8}

.

Xem đáp án

Chọn A

Hàm số $y = \sin (a x + b)$ tuần hoàn với chu kì $T = \frac{2 π}{|a|}$ .

Hàm số $y = \sin (5 x - \frac{π}{4})$ tuần hoàn với chu kì $T = \frac{2 π}{5}$ .

Câu 4:

Chu kỳ của hàm số y = tan x là:

A.

2 π

.

B.

\frac{π}{4}

.

C.

k π, k \in ℤ

.

D.

π

.

Xem đáp án

Chọn D

Câu 5:

Đường cong trong hình dưới đây là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn phương án

Hỏi hàm số đó là hàm số nào?

A.

y = 1 + \sin 2 x .

B. y = cos x

C. y = - sin x

D. y = - cos x

Xem đáp án

Chọn B

Đồ thị hàm số đi qua ba điểm $(0; 1); (\frac{π}{2}; 0); (π; 1)$ . Chỉ có hàm số y = cos x thỏa mãn.

Câu 6:

Phương trình

s in x = \sin α

có nghiệm là

A. $[\begin{array}{l} x = α + k 2 π \\ x = π - α + k 2 π \end{array}; k \in ℤ$

B.

[\begin{array}{l} x = α + k π \\ x = π - α + k π \end{array}; k \in ℤ

.

C.

[\begin{array}{l} x = α + k π \\ x = - α + k π \end{array}; k \in ℤ

.

D.

[\begin{array}{l} x = α + k 2 π \\ x = - α + k 2 π \end{array}; k \in ℤ

.

Xem đáp án

Chọn A

Câu 7:

Phương trình

\tan x = \tan α

có nghiệm là

A. $x = α + k π, k \in ℤ .$

B.

x = α + k 2 π, k \in ℤ .

C.

x = - α + k π, k \in ℤ .

D.

x = \arctan α + k π, k \in ℤ .

Xem đáp án

Chọn A

Câu 8:

Nghiệm của phương trình

\cos x = - \frac{1}{2}

là

A. $x = \pm \frac{π}{3} + k 2 π, k \in ℤ .$

B.

x = \pm \frac{2 π}{3} + k 2 π, k \in ℤ .

C.

x = \pm \frac{π}{6} + k 2 π, k \in ℤ .

D.

x = \pm \frac{π}{6} + k π, k \in ℤ .

Xem đáp án

Chọn B

Ta có $\cos x = - \frac{1}{2} \Leftrightarrow \cos x = \cos \frac{2 π}{3} \Leftrightarrow x = \pm \frac{2 π}{3} + k 2 π, k \in ℤ .$

Câu 9:

Nghiệm của phương trình cot x = tan x là

A.

x = \frac{π}{4} + k \frac{π}{4}, k \in ℤ .

B.

x = \frac{π}{4} + k \frac{π}{2}, k \in ℤ .

C.

x = \frac{π}{4} + k π, k \in ℤ .

D.

x = \frac{π}{4} + k 2 π, k \in ℤ .

Xem đáp án

Chọn B

Điều kiện $\{\begin{cases} \cos x \neq 0 \\ \sin x \neq 0 \end{cases} \Leftrightarrow x \neq k \frac{π}{2}, k \in ℤ .$

Ta có $\cot x = \tan x \Leftrightarrow \cot x = \cot (\frac{π}{2} - x) \Leftrightarrow x = \frac{π}{2} - x + k π \Leftrightarrow x = \frac{π}{4} + k \frac{π}{2}, k \in ℤ . (t m d k)$

Câu 10:

Phương trình nào trong số các phương trình sau có nghiệm?

A. $\sin x + 3 \cos x = 6$ .

B.

2 \sin x - 3 \cos x = 1

.

C.

\sin x = \sqrt{2}

.

D.

\cos x + 3 = 0

.

Xem đáp án

Chọn B

Ta có $\{\begin{cases} - 1 \leq \sin x \leq 1 \\ - 1 \leq \cos x \leq 1 \end{cases}$ nên hai phương trình ở C và D vô nghiệm.

Phương trình lượng giác dạng $a \sin x + b \cos x = c$ có nghiệm khi $a^{2} + b^{2} \geq c^{2}$ .

Đáp án A: $1^{2} + 3^{2} < 6^{2}$ nên phương trình vô nghiệm.

Đáp án B: $2^{2} + {(- 3)}^{2} > 1$ nên phương trình có nghiệm.

Câu 11:

Trong một hộp chứa 6 quả cầu trắng được đánh số từ 1 đến 6 và ba quả cầu đen được đánh số 7, 8, 9. Có bao nhiêu cách chọn một

trong các quả cầu ấy?

A. 1

B. 7

C. 6

D. 9

Xem đáp án

Chọn D

Chọn 1 quả cầu trắng trong 6 quả có 6 cách chọn.

Chọn 1 quả cầu đen trong 3 quả có 3 cách chọn.

Do đó, số cách chọn một trong các quả cầu là 6 + 3 = 9 (cách)

Câu 12:

Từ thành phố A tới thành phố B có 3 con đường, từ thành phố B tới thành phố C có 4 con đường. Hỏi có bao nhiêu cách đi từ

A tới C qua B?

A. 24

B. 7

C. 6

D. 12

Xem đáp án

Chọn D

Từ A đến B có 3 cách chọn đường đi, từ B đến C có 4 cách chọn đường đi.

Nên số cách đi từ A tới C qua B là 3.4 = 12 (cách)

Câu 13:

Cho tập hợp A có n phần tử

(n \geq 1) .

Số tập con gồm

k (0 \leq k \leq n)

phần tử của tập kđược xác định bởi công thức?

A.

C_{n}^{k} = \frac{n!}{(n - k)! k!} .

B.

A_{n}^{k} = \frac{n!}{(n - k)!} .

C.

A_{n}^{k} = \frac{n!}{(n - k)! k!} .

D.

C_{n}^{k} = \frac{n!}{(n - k)!} .

Xem đáp án

Chọn A

Mỗi tập hợp con gồm kphần tử của tập Acó nphần tử $(n \geq 1)$ là một tổ hợp chập k của nphần tử. Do đó số tập con gồm kphần tử của tập Ađược xác định bởi công thức $C_{n}^{k} = \frac{n!}{(n - k)! k!} .$

Câu 14:

Cho tập A có n phần tử

(n \geq 1)

. Số kết quả của việc sắp xếp thứ tự n phần tử của tập hợp A là:

A.

\frac{n!}{(n - 1)}

.

B.

(n - 1)!

C.

n!

.

D.

\frac{n!}{(n - 1)!} .

Xem đáp án

Chọn C

Kết quả của việc sắp thứ tự n phần tử của tập hợp A là các hoán vị của tập hợp A.

Tập hợp A có n phần tử thì có $n!$ hoán vị.

Câu 15:

Biết

C_{n}^{3} = 35.

Vậy

A_{n}^{3}

bằng bao nhiêu?

A. 35

B. 45

C. 210

D. 70

Xem đáp án

Chọn C

Ta có: $A_{n}^{k} = \frac{n!}{(n - k)!}; C_{n}^{k} = \frac{n!}{k! (n - k)!}$

Suy ra $A_{n}^{k} = C_{n}^{k} . k!$ ; k = 3 nên $A_{n}^{3} = C_{n}^{3} .3! = 35.6 = 210$

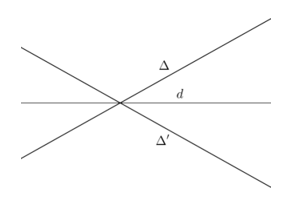
Câu 16:

Trong mặt phẳng Oxy, cho $\vec{v} = (a, b) .$ Giả sử phép tịnh tiến theo $\vec{v}$ biến M (x ;y) thành điểm M'(x ; y). Ta có biểu thức tọa độ của phép tịnh tiến theo vectơ $\vec{v}$ là:

A

\{\begin{cases} x = x' + a \\ y = y' + b \end{cases}

B.

\{\begin{cases} x' = x + a \\ y' = y + b \end{cases}

C.

\{\begin{cases} x' - b = x + a \\ y' - a = y + b \end{cases}

D.

\{\begin{cases} x' + b = x + a \\ y' + a = y + b \end{cases}

Xem đáp án

Chọn B

Câu 17:

Tìm mệnh đề sai trong các mệnh đề sau:

A. Phép đối xứng trục bảo toàn khoảng cách giữa hai điểm bất kì.

B. Phép đối xứng trục biến một đường thẳng thành một đường thẳng song song hoặc trùng với đường thẳng đã cho.

C. Phép đối xứng trục biến tam giác thành tam giác bằng tam giác đã cho.

D. Phép đối xứng trục biến đường tròn thành đường tròn bằng đường tròn đã cho.

Xem đáp án

Chọn B

Câu B sai vì thiếu trường hợp đường thẳng và trục đối xứng hợp nhau góc nhọn thì trục đối xứng là đường phân giác của đường thẳng và ảnh của nó.

Tìm mệnh đề sai trong các mệnh đề sau: A. Phép đối xứng trục bảo toàn khoảng cách giữa hai điểm bất kì. (ảnh 1)

Câu 18:

Khẳng định nào sau đây đúng về phép đối xứng tâm:

A. Nếu OM = OM' thì M' là ảnh của M qua phép đối xứng tâm O.

B. Nếu

\vec{O M} = - \vec{O M'}

thì M' là ảnh của M qua phép đối xứng tâm O.

C. Phép quay là phép đối xứng tâm.

D. Phép đối xứng tâm không phải là phép quay.

Xem đáp án

Chọn B

Nếu $\vec{O M} = - \vec{O M'}$ thì O là trung điểm của đoạn thẳng MM' do đó M' là ảnh của M qua phép đối xứng tâm O.

Câu 19:

Cho tam giác ABC các đỉnh theo thứ tự cùng chiều quay của kim đồng hồ. Hãy xác định góc quay của phép quay tâm A biến

B thành C.

A.

30^{0} .

B.

300^{0} .

hoặc

- 60^{0} .

C.

120^{0} .

D.

90^{0} .

Xem đáp án

Chọn B

Câu 20:

Cho phép vị tự

4 \vec{I A} = 5 \vec{I B}

.Phép vị tự tâm I tỉ số k biến A thành B. Tìm k?

A. $- \frac{5}{4} .$

B.

\frac{5}{4} .

C.

- \frac{4}{5} .

D.

\frac{4}{5} .

Xem đáp án

Chọn D

$4 \vec{I A} = 5 \vec{I B} \Leftrightarrow \vec{I B} = \frac{4}{5} \vec{I A} \Rightarrow k = \frac{4}{5} .$

Câu 21:

Xét sự biến thiên của hàm số y = tan 2x. Khẳng định nào sau đây đúng:

A.Hàm số đã cho đồng biến trên $(0; \frac{π}{4})$ và $(\frac{π}{4}; \frac{π}{2})$ .

B.Hàm số đã cho đồng biến trên

(0; \frac{π}{4})

và nghịch biến trên

(\frac{π}{4}; \frac{π}{2})

.

C.Hàm số đã cho luôn đồng biến trên

(0; \frac{π}{2})

.

D.Hàm số đã cho nghịch biến trên

(0; \frac{π}{4})

và đồng biến trên

(\frac{π}{4}; \frac{π}{2})

.

Xem đáp án

Chọn A

Tập xác định $D = ℝ \ \{\frac{π}{4} + k \frac{π}{2} | k \in Z\} .$

Dựa vào bản biến thiên y = tan x ta suy ra sự biến thiên của hàm y = tan 2x. Hàm số đã cho đồng biến trên $(0; \frac{π}{4})$ và $(\frac{π}{4}; \frac{π}{2})$ .

Câu 22:

Tìm tất cả các giá trị nguyên của tham số m để phương trình cos x = m - 1 có nghiệm.

A. $- 1 \leq m \leq 1$ .

B. Vô số.

C.

m \in \{0; 1; 2\}

.

D.

m \in \{- 1; 0; 1\}

.

Xem đáp án

Chọn C

Câu 23:

Tìm tất cả các giá trị nguyên của tham số m để phương trình

\sin^{2} x = m

có nghiệm.

A. $m \in \{1; 2\}$ .

B.

m \in \{- 1; 0; 1\}

.

C.

m \in \{0; 1\}

.

D. Vô số.

Xem đáp án

Chọn C

Ta có: $0 \leq \sin^{2} x \leq 1$ nên phương trình đã cho có nghiệm $\Leftrightarrow 0 \leq m \leq 1$ .

$m \in ℤ \Rightarrow m \in \{0; 1\}$

Câu 24:

Nghiệm của phương trình

\cos x = - \frac{1}{2}

là:

A. $x = \pm \frac{2 π}{3} + k 2 π, k \in ℤ$ .

B.

x = \pm \frac{π}{6} + k π, k \in ℤ

.

C.

x = \pm \frac{π}{3} + k 2 π, k \in ℤ

.

D.

x = \pm \frac{π}{6} + k 2 π, k \in ℤ

.

Xem đáp án

Chọn A

$\cos x = - \frac{1}{2} \Leftrightarrow \cos x = \cos \frac{2 π}{3} \Leftrightarrow x = \pm \frac{2 π}{3} + k 2 π, k \in ℤ$ .

Câu 25:

Phương trình

\cos 2 x + 5 \sin x - 4 = 0

có bao nhiêu nghiệm trên khoảng

(0; 10 π)

?

A. 5

B. 4

C. 6

D. 3

Xem đáp án

Chọn A

Câu 26:

Nghiệm của phương trình

\sin x + \sqrt{3} \cos x = \sqrt{2}

là:

A. $x = - \frac{π}{12} + k 2 π; x = \frac{5 π}{12} + k 2 π$ .

B.

x = - \frac{π}{4} + k 2 π; x = \frac{3 π}{4} + k 2 π

.

C.

x = \frac{π}{3} + k 2 π; x = \frac{2 π}{3} + k 2 π

.

D.

x = - \frac{π}{4} + k 2 π; x = - \frac{5 π}{4} + k 2 π

.

Xem đáp án

Chọn A

$\sin x + \sqrt{3} \cos x = \sqrt{2}$ $\Leftrightarrow \frac{1}{2} \sin x + \frac{\sqrt{3}}{2} \cos x = \frac{\sqrt{2}}{2} \Leftrightarrow \cos \frac{π}{3} . \sin x + \sin \frac{π}{3} . \cos x = \sin \frac{π}{4}$

$\Leftrightarrow \sin (x + \frac{π}{3}) = \sin \frac{π}{4} \Leftrightarrow [\begin{array}{l} x + \frac{π}{3} = \frac{π}{4} + k 2 π \\ x + \frac{π}{3} = \frac{3 π}{4} + k 2 π \end{array} \Leftrightarrow [\begin{array}{l} x = - \frac{π}{12} + k 2 π \\ x = \frac{5 π}{12} + k 2 π \end{array} (k \in ℤ)$ .

Câu 27:

Từ thành phố A đến thành phố B có 4 con đường, từ thành phố A đến thành phố C có 3 con đường, từ thành phố B đến thành phố D có 2 con đường, từ thành phố C đến thành phố D có 3 con đường, không có con đường nào nối từ thành phố B đến thành phố C. Hỏi có bao nhiêu con đường đi từ thành phố A đến thành phố D.

A. 12

B. 17

C. 18

D. 72

Xem đáp án

Chọn B

Số cách đi từ A đến D qua B là 4.2 = 8.

Số cách đi từ A đến D qua C là 3.3 = 9.

Nên số cách đi từ A đến D là: 8 + 9 = 17 cách.

Câu 28:

Người ta trồng cây theo hình tam giác với quy luật: ở hàng thứ nhất có 1 cây, ở hàng thứ hai có 2 cây, ở hàng thứ ba có 3 cây,… ở hàng thứ n có n cây. Biết rằng người ta trồng hết 4950 cây. Hỏi số hàng cây được trồng theo cách trên là bao nhiêu?

A. 99

B. 100

C. 101

D. 98

Xem đáp án

Chọn A

Ta thấy số cây ở mỗi hàng tạo nên một cấp số cộng có số hạng đầu $u_{1} = 1$ và công sai d = 1.

Ta có $S_{n} = \frac{(2 u_{1} + (n - 1) d) n}{2} \Rightarrow \frac{n^{2} + n}{2} = 4950$ $\Leftrightarrow n^{2} - n - 9900 = 0 \Rightarrow n = 99$ .

Câu 29:

Một tổ có 6 học sinh nam và 9 học sinh nữ. Hỏi có bao nhiêu cách chọn 6 học sinh đi lao động, trong đó có 2 học sinh nam?

A. $C_{6}^{2} + C_{9}^{4}$ .

B.

C_{6}^{2} . C_{9}^{4}

.

C.

A_{6}^{2} . A_{9}^{4}

.

D.

C_{9}^{2} C_{6}^{4}

.

Xem đáp án

Chọn B

Chọn 4 học sinh nữ có $C_{9}^{4}$ cách, chọn 2 học sinh nam có $C_{6}^{2}$ cách.

Có $C_{6}^{2} . C_{9}^{4}$ cách chọn 6 học sinh đi lao động, trong đó 2 học sinh nam.

Câu 30:

Có bao nhiêu cách xếp 6 bạn A, B, C, D, E, F vào một ghế dài sao cho bạn A, F ngồi ở 2 đầu ghế?

A. 120

B. 720

C. 24

D. 48

Xem đáp án

Chọn D

Có $2!$ cách xếp bạn A, F ngồi ở 2Vđầu ghế

Có $4!$ cách xếp 4 bạn vào 4 vị trí còn lại

Vậy: Có $2! .4! = 48$ (cách xếp).

Câu 31:

Cho điểm M (1;-2). Tọa độ M' là ảnh của điểm M qua phép tịnh tiến theo vectơ

\vec{v} = (3; - 2)

.

A. $M^{'} (4; 4)$ .

B.

M^{'} (- 2; 4)

.

C.

M^{'} (4; - 4)

.

D.

M^{'} (- 2; 0)

.

Xem đáp án

Chọn C

$T_{\vec{v}} (M) = M^{'} (x; y) \Leftrightarrow \vec{M M'} = \vec{v}$ $\Leftrightarrow \{\begin{cases} x^{'} = 1 + 3 = 4 \\ y^{'} = - 2 + (- 2) = - 4 \end{cases} \Rightarrow M^{'} (4; - 4)$ .

Câu 32:

Cho điểm M (2;-3). Tìm tọa độ điểm M' là ảnh của điểm M qua phép đối xứng trục Ox.

A.

M^{'} (- 2; - 3) .

B.

M^{'} (2; 3) .

C.

M^{'} (- 2; 3) .

D.

M^{'} (2; 0) .

Xem đáp án

Chọn B

Câu 33:

Cho điểm M(3;1). Tìm tọa độ điểm N là ảnh của M qua phép đối tâm O.

A.

N (- 3; - 1) .

B.

N (- 3; 1) .

C.

N (0; 1) .

D.

N (3; - 5) .

Xem đáp án

Chọn A
Ta có gốc O là trung điểm của đoạn thẳng MN. Suy ra N(-3;1)

Câu 34:

Cho tam giác ABC đều với trọng tâm G. Phép quay tâm G với góc quay nào dưới đây biến tam giác ABC thành chính nó?

A. $30^{0}$ .

B.

120^{0}

.

C.

60^{0}

.

D.

45^{0}

.

Xem đáp án

Chọn B

Ta thấy phép quay tâm G góc quay $120^{0}$ biến điểm A thành điểm B, biến điểm B thành điểm C, biến điểm C thành điểm A.

Do đó, phép quay tâm G góc quay $120^{0}$ biến tam giác ABC thành chính nó.

Câu 35:

Cho tam giác ABC với trọng tâm G. Gọi A',B',C'lần lượt là trung điểm của các cạnh BC,AC, AB của tam giác ABC. Khi đó, phép vị tự nào biến tam giác A'B'C' thành tam giác ABC?

A. Phép vị tự tâm G, tỉ số k = 2.

B. Phép vị tự tâm G, tỉ số k = -2.

C. Phép vị tự tâm G, tỉ số k = -3.

D. Phép vị tự tâm G, tỉ số k = 3.

Xem đáp án

Chọn B

Ta có: $V_{(G, k)} (A') = A$ .

$\Rightarrow \vec{G A} = k \vec{G A'}$ .

Mà $\vec{G A}, \vec{G A'}$ ngược hướng và $G A = 2 G A'$ .

$\Rightarrow k = - 2$ .

Câu 36:

Giải phương trình lượng giác:

cosx . c o s \frac{x}{2} . \cos \frac{3 x}{2} - \sin x . \sin \frac{x}{2} . \sin \frac{3 x}{2} = \frac{1}{2}

.

Xem đáp án

Giải phương trình lượng giác: cos x . cos x/2 . cos 3x/2 - sin x . sin 3x/2 = 1/2 . (ảnh 1)

Câu 37:

Trong mặt phẳng tọa độ Oxy, cho hai đường thẳng $(Δ) : 2 x - y + 1 = 0$ và $(d) : 2 x - y - 1 = 0$ . Tìm tọa độ $\vec{v}$ có giá vuông góc với $(Δ)$ để $T_{\vec{v}} (Δ) = (d)$ .

Xem đáp án

Trong mặt phẳng tọa độ Oxy, cho hai đường thẳng đenta: 2x -y +1 = 0 và d: 2x - y - 1 = 0 . Tìm tọa độ vecto v có giá vuông góc với (ảnh 1)

Câu 38:

Cho tập $A = {0,1,2,3,4,5,6,7,8,9}$ . Từ các phần tử của tập A có thể lập được bao nhiêu số có 6 chữ số đôi một khác nhau mà trong đó hai số chẵn không được đứng cạnh nhau?

Xem đáp án

Cho tập A= 0;1;2;3;4;5;6;7;8;9 . Từ các phần tử của tập A có thể lập được bao nhiêu số có 6 chữ số đôi một khác nhau mà trong đó hai số chẵn không được đứng cạnh nhau? (ảnh 1)

Câu 39:

Một chiếc hộp đựng 20 viên bi giống nhau, mỗi viên bi được ghi một trong các số tự nhiên từ 1 đến 20 (không có hai viên bi ghi cùng một số). Tính số cách bốc được 4 viên bi từ chiếc hộp nói trên sao cho tổng các số ghi trên các viên bi chia hết cho 3.

Xem đáp án

Bộ 20 đề thi giữa học kì 1 Toán 11 năm 2022 - 2023 có đáp án

Bộ 20 đề thi giữa học kì 1 Toán 11 năm 2022 - 2023 có đáp án (Đề 2)

Danh sách câu hỏi

Bài thi liên quan

Có thể bạn quan tâm

Các bài thi hot trong chương