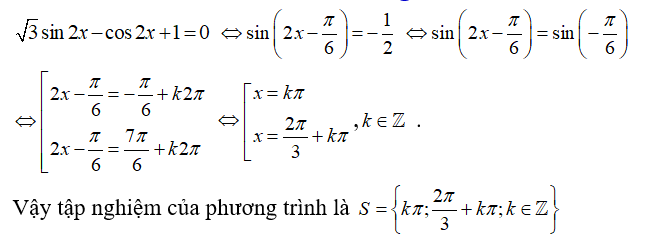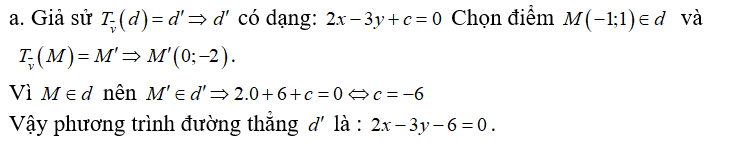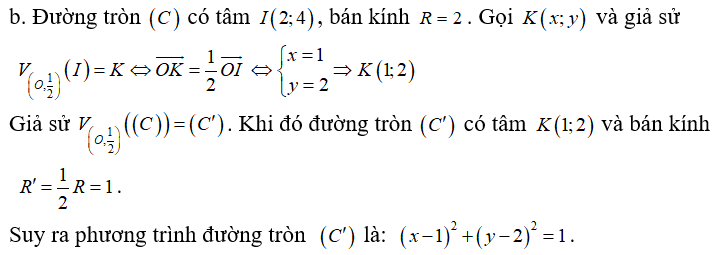44 câu hỏi trắc nghiệm thuộc Bộ 20 đề thi giữa học kì 1 Toán 11 năm 2022

Câu 1:

Giải phương trình $\sqrt{3} + 3 \tan x = 0$ .

A. $x = \frac{π}{2} + k π (k \in ℤ)$ .

B.

x = \frac{π}{3} + k π (k \in ℤ)

.

C.

x = \frac{π}{2} + k 2 π (k \in ℤ)

.

D.

x = - \frac{π}{6} + k π (k \in ℤ)

.

Xem đáp án

Chọn D

Ta có: $\tan x = - \frac{\sqrt{3}}{3} \Leftrightarrow \tan x = \tan (- \frac{π}{6}) \Leftrightarrow x = - \frac{π}{6} + k π, k \in ℤ$

Câu 2:

Công thức nào dưới đây là công thức nghiệm của phương trình $\sin x = \sin α$ ?

A. $x = \pm α + k 2 π, k \in ℤ$ .

B.

[\begin{array}{l} x = α + k 2 π \\ x = π - α + k 2 π \end{array}, k \in ℤ

.

C.

[\begin{array}{l} x = α + k π \\ x = π - α + k π \end{array}, k \in ℤ

.

D.

x = α + k π, k \in ℤ

.

Xem đáp án

Chọn B

$\sin x = \sin α \Leftrightarrow [\begin{array}{l} x = α + k 2 π \\ x = π - α + k 2 π \end{array}, k \in ℤ$

Câu 3:

Phương trình $2 \sin^{2} x - 5 \sin x \cos x - \cos^{2} x = - 2$ tương đương với phương trình nào sau đây?

A. $3 \cos 2 x - 5 \sin 2 x = 5$ .

B.

3 \cos 2 x + 5 \sin 2 x = - 5

.

C.

3 \cos 2 x - 5 \sin 2 x = - 5

.

D.

3 \cos 2 x + 5 \sin 2 x = 5

.

Xem đáp án

Chọn D

$2 \sin^{2} x - 5 \sin x \cos x - \cos^{2} x = - 2$

$\Leftrightarrow 2 (\frac{1 - \cos 2 x}{2}) - 5 (\frac{1}{2} \sin 2 x) - (\frac{1 + \cos 2 x}{2}) = - 2$

$\Leftrightarrow 3 \cos 2 x + 5 \sin 2 x = 5$

Câu 4:

Đường cong trong hình dưới đây là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn phương án A, B, C, D. Hỏi hàm số đó là hàm số nào?

A. y = 1 + sin 2x.

B. y = cos x.

C. y = -sin x.

D. y = -cos x.

Xem đáp án

Chọn B

Vì chu kì của hàm số là $2 π$ nên loại A

-sin 0 = 0 nên loại C

-cos 0 = -1 nên loại D

Câu 5:

Hàm số y = tan x đồng biến trên khoảng/ đoạn nào sau đây?

A. $(\frac{π}{2}; \frac{3 π}{2})$ .

B.

(π; 2 π)

.

C.

[- \frac{π}{2}; \frac{π}{2}]

.

D.

[0; π]

.

Xem đáp án

Chọn A

$\tan \frac{π}{2}$ không xác định nên loại C, D

$\tan \frac{3 π}{2}$ không xác định nên loại B

Câu 6:

Tìm tất cả các họ nghiệm của phương trình

\sin x - \sqrt{3} \cos x = 0

.

A. $x = \frac{π}{3} + k 2 π, k \in ℤ$ .

B.

x = \frac{π}{6} + k π, k \in ℤ

.

C.

x = \frac{π}{3} + k π, k \in ℤ

.

D.

x = \frac{π}{6} + k 2 π, k \in ℤ

.

Xem đáp án

Chọn C

Ta có $\sin x - \sqrt{3} \cos x = 0 \Leftrightarrow$ $\tan x = \sqrt{3} \Leftrightarrow$ $x = \frac{π}{3} + k π, k \in ℤ$ .

Câu 7:

Trong các phương trình được liệt kê ở các phương án dưới đây, phương trình nào vô nghiệm?

A. 2017 sin x + 2016 = 0.

B. sinx = cosx.

C. cot x = 2.

D. 3cosx - 4 = 0.

Xem đáp án

Chọn D

Ta có $3 \cos x - 4 = 0 \Leftrightarrow \cos x = \frac{4}{3}$ . Do $\frac{4}{3} > 1$ nên phương trình vô nghiệm.

Câu 8:

Tìm m để phương trình cosx - 2m+ 1 = 0 có nghiệm.

A. $m > - \frac{1}{2}$ .

B.

0 < m < 1

.

C.

0 \leq m \leq 1

.

D.

m \geq - \frac{1}{2}

.

Xem đáp án

Chọn C

Ta có $\cos x - 2 m + 1 = 0$ $\Leftrightarrow \cos x = 2 m - 1$ có nghiệm khi và chỉ khi

$- 1 \leq 2 m - 1 \leq 1 \Leftrightarrow$ $0 \leq 2 m \leq 2$ $0 \leq m \leq 1$ .

Câu 9:

Phương trình tan 5x - tan x = 0 có bao nhiêu nghiệm trên

[0; π)

?

A. 3

B. 4

C. 5

D. 2

Xem đáp án

Chọn A

Câu 10:

Gọi M và m lần lượt là giá trị lớn nhất và nhỏ nhất của hàm số

y = \frac{1}{2} \sin 2 x - 1

trên R. Tính giá trị của biểu thức P = M + m.

A. 1

B. -2

C. -1

D. 0

Xem đáp án

Chọn B

Câu 11:

Trong 3 phương trình được cho dưới đây, có bao nhiêu phương trình vô nghiệm?

$(I) \cos x = \sqrt{5} - \sqrt{3}$ ; $(I I) \sin x = 1 - \sqrt{2}$ ; $(I I I) \sin x + \cos x = 2$ .

A. 1

B. 2

C. 3

D. 0

Xem đáp án

Chọn A

Ta có $- \sqrt{2} \leq \sin x + \cos x \leq \sqrt{2}$ nên phương trình (III) vô nghiệm.

Câu 12:

Tìm tập xác định của hàm số $y = \frac{1}{\sin x - 1}$ .

A. $D = ℝ \ \{1\}$ .

B.

D = ℝ \ \{\frac{π}{2}\}

.

C.

D = ℝ \ \{\frac{π}{2} + k 2 π, k \in ℤ\}

.

D.

D = ℝ \ \{\frac{π}{2} + k π, k \in ℤ\}

.

Xem đáp án

Chọn C

ĐK: $\sin x - 1 \neq 0 \Leftrightarrow \sin x \neq 1$ $\Leftrightarrow x \neq \frac{π}{2} + k 2 π, k \in ℤ$ .

TXĐ: $D = ℝ \ \{\frac{π}{2} + k 2 π, k \in ℤ\}$ .

Câu 13:

Tìm tập giá trị của hàm số y = cos 2x.

A. [-1;1].

B. (-1;1).

C. [-2;2].

D.

[\frac{- 1}{2}; \frac{1}{2}]

.

Xem đáp án

Chọn A

Câu 14:

Điều kiện để phương trình $a \cos x + b \sin x = c (a^{2} + b^{2} \neq 0)$ vô nghiệm là

A. $a^{2} + b^{2} \leq c^{2}$ .

B.

a^{2} + b^{2} < c^{2}

.

C.

a^{2} + b^{2} = c^{2}

.

D.

a^{2} + b^{2} \geq c^{2}

.

Xem đáp án

Chọn B

Câu 15:

Biết rằng khi $m = m_{0}$ thì phương trình $2 \sin^{2} x - (5 m + 1) \sin x + 2 m^{2} + 2 m = 0$ có đúng 5 nghiệm thuộc khoảng $(- \frac{π}{2}; 3 π)$ . Mệnh đề nào sau đây đúng?

A. $m_{0} \in (- \frac{3}{5}; - \frac{2}{5})$ .

B.

m_{0} = \frac{1}{2}

.

C.

m_{0} \in (\frac{3}{5}; \frac{7}{10}]

.

D.

m_{0} = - 3

.

Xem đáp án

Chọn B

Câu 16:

Gọi $x_{0}$ là nghiệm dương nhỏ nhất của phương trình $\frac{2 \cos 2 x}{1 - \sin 2 x} = 0$ . Mệnh đề nào sau đây đúng?

A. $x_{0} \in [\frac{π}{4}; \frac{π}{2}]$ .

B.

x_{0} \in (\frac{π}{2}; \frac{3 π}{4})

.

C.

x_{0} \in [\frac{3 π}{4}; π]

.

D.

x_{0} \in (0; \frac{π}{4})

.

Xem đáp án

Chọn C

Điều kiện: $\sin 2 x \neq 1 \Leftrightarrow 2 x \neq \frac{π}{2} + k 2 π \Leftrightarrow x \neq \frac{π}{4} + k π$ .

Trong điều kiện đó phương trình suy ra $\cos 2 x = 0 \Leftrightarrow 2 x = \frac{π}{2} + k π \Leftrightarrow x = \frac{π}{4} + k \frac{π}{2}$

Kết hợp điều kiện suy ra $x = \frac{3 π}{4} + k π$ .

Vậy nghiệm dương nhỏ nhất của phương trình là: $x_{0} = \frac{3 π}{4} \in [\frac{3 π}{4}; π]$ .

Câu 17:

Gọi m,M lần lượt là giá trị nhỏ nhất và lớn nhất của hàm số $y = {(3 - 5 \sin x)}^{2018}$ trên R . Tính $S = 2018 m + M$ .

A. $S = 2^{2018} (1 + 2^{4036})$ .

B.

S = 2^{2018}

.

C.

S = 2^{4036}

.

D.

S = 2^{6054}

.

Xem đáp án

Chọn D

Ta thấy ${(3 - 5 \sin x)}^{2018} \geq 0$ và $3 - 5 \sin x = 0 \Leftrightarrow \sin x = \frac{3}{5}$ (có nghiệm) nên giá trị nhỏ nhất của hàm số là m = 0 .

Dễ thấy giá trị lớn nhất của hàm số đạt được khi sinx = -1, suy ra $M = 8^{2018}$ $= 2^{6054}$ .

Câu 18:

Tìm tập xác định D của hàm số $y = \frac{1 - \sin x}{1 + \cos x}$ .

A. $D = ℝ \ \{- \frac{π}{2} + k 2 π; \frac{π}{2} + k 2 π, k \in ℤ\}$ .

B.

D = ℝ \ \{- k π, k \in ℤ\}

.

C.

D = ℝ \ \{π + k 2 π, k \in ℤ\}

.

D.

D = ℝ \ \{\frac{π}{2} + k 2 π, k \in ℤ\}

.

Xem đáp án

Chọn C

Điều kiện xác định của hàm số: $\cos x \neq - 1 \Leftrightarrow x \neq π + k 2 π$ .

Câu 19:

Tính tổng T tất cả các nghiệm của phương trình $\cos^{2} x - \sin 2 x = \sqrt{2} + \sin^{2} x$ trên $(0; 2 π)$ .

A. $T = \frac{21 π}{8}$ .

B.

T = \frac{11 π}{4}

.

C.

T = \frac{3 π}{4}

.

D.

T = \frac{7 π}{8}

.

Xem đáp án

Chọn B

Câu 20:

Có bao nhiêu giá trị nguyên của tham số m thuộc đoạn $[- 10; 10]$ để phương trình $11 \sin^{2} x + (m - 2) \sin 2 x + 3 \cos^{2} x = 2$ có nghiệm?

A. 6

B. 21

C. 15

D. 16

Xem đáp án

Chọn D

Câu 21:

Trong mặt phẳng tọa độ Oxy cho điểm A(3;0) . Tìm tọa độ điểm A' là ảnh của điểm A qua phép quay tâm O(0;0) góc quay $\frac{π}{2}$ .

A. $A' (2 \sqrt{3}; 2 \sqrt{3})$ .

B. A'(0;-3).

C. A'(0;3).

D. A'(-3;0).

Xem đáp án

Chọn C

Ta có theo định nghĩa phép quay: $\{\begin{cases} O A = O A' \\ (O A'; O A) = + \frac{π}{2} \end{cases}$ $\Rightarrow A' (0; 3)$ .

Câu 22:

Trong mặt phẳng tọa độ Oxy nếu phép tịnh tiến biến điểm A(3;2) thànhđiểmA'(2;3) thì nó biến điểm B(2;5) thành điểm:

A. B'(1;6).

B. B'(5;5).

C. B'(1;1).

D. B'(5;2).

Xem đáp án

Chọn A

Câu 23:

Tính chất nào sau đây không phải là tính chất của phép dời hình?

A. Biến đường tròn thành đường tròn bằng nó.

B. Biến tam giác thành tam giác bằng nó, biến tia thành tia.

C. Biến đoạn thẳng thành đoạn thẳng có độ dài gấp k lần đoạn thẳng ban đầu

(k \neq 1)

D. Biến ba điểm thẳng hàng thành ba điểm thẳng hàng và bảo toàn thứ tự của ba điểm đó.

Xem đáp án

Chọn C

Câu 24:

Trong mặt phẳng tọa độ Oxy cho điểm $J (1; \sqrt{2})$ và đường tròn $(C) : x^{2} + y^{2} - 4 x + 10 y + 14 = 0$ . Phép vị tự tâm J tỷ số $k = - \sqrt{3}$ biến đường tròn (C) thành đường tròn (C'). Tìm bán kính R của (C')?

A. $R = \sqrt{129}$ .

B.

R = 3 \sqrt{5}

.

C.

R = 15 \sqrt{3}

.

D.

R = \sqrt{15}

.

Xem đáp án

Chọn B

Đường tròn (C) có bán kính $r = \sqrt{4 + 25 - 14} = \sqrt{15}$ .

Khi đó $R = |- \sqrt{3}| r = 3 \sqrt{5}$ .

Câu 25:

Cho hình bình hành ABCD . Phép tịnh tiến $T_{\vec{D A}}$ biến:

A. C thành A .

B. C thành B .

C. A thành D .

D. B thành C .

Xem đáp án

Chọn B

Câu 26:

Mọi phép dời hình cũng là phép đồng dạng với tỉ số k bằng

A. k = 2.

B. k = -1.

C. k = 0.

D. k = 1.

Xem đáp án

Chọn D.

Xét phéo dời hình F mà $F (A) = A', F (B) = B' \Rightarrow A' B' = A B \Rightarrow k = 1$ .

Câu 27:

Trong mặt phẳng tọa độ Oxy cho hai điểm $A (- 2; - 3), B (4; 1)$ . Phép đồng dạng tỉ số $k = \frac{1}{2}$ biến điểm A thành A', biến điểm B thành B'. Tính độ dài A'B'

A. $A' B' = \frac{\sqrt{50}}{2}$ .

B.

A' B' = \sqrt{50}

.

C.

A' B' = \frac{\sqrt{52}}{2}

.

D.

A' B' = \sqrt{52}

.

Xem đáp án

Chọn C.

Theo giả thiết ta có $A' B' = |k| A B = \frac{1}{2} . \sqrt{{(4 + 2)}^{2} + {(1 + 3)}^{2}} = \frac{\sqrt{52}}{2}$ .

Câu 28:

Mệnh đề nào sau đây là sai?

A. Hai đường thẳng bất kì luôn đồng dạng.

B. Hai đường tròn bất kì luôn đồng dạng.

C. Hai hình vuông bất kì luôn đồng dạng.

D. Hai hình chữ nhật bất kì luôn đồng dạng.

Xem đáp án

ChọnD.

D sai vì nếu chọn hai hình chữ nhật ABCD và A'B'C'D' có chiều dài chiều rộng tương ứng là AB,CD và A'B',C'D' mà $\frac{A B}{C D} \neq \frac{A' B'}{C' D'}$ thì không tồn tại phép đồng dạng nào biến hình nhày thành hình kia, hay hai hình chữ nhật này không đồng dạng nhau .

Câu 29:

Cho tam giác đều ABC tâm O. Có bao nhiêu phép quay tâm O góc $α$ với $0 \leq α < 2 π$ , biến tam giác ABC thành chính nó?

A. 2

B. 3

C. 4

D. 1

Xem đáp án

Chọn B.

Các phép quay tâm O góc $α$ , với $α \in \{0; \frac{2 π}{3}; \frac{4 π}{3}\}$ biến tam giác ABC thành chính nó.

Câu 30:

Cho phép biến hình F có quy tắc đặt tương ứng với mỗi điểm $M (x_{M}; y_{M})$ có ảnh là điểm $M^{'} (x^{'}; y^{'})$ theo công thức $F : \{\begin{cases} x^{'} = x_{M} \\ y^{'} = y_{M} + 1 \end{cases}$ . Tính độ dài đoạn thẳng PQ với P,Q tương ứng là ảnh của hai điểm $A (1; - 2), B (- 1; 0)$ qua phép biến hình F.

A. $P Q = 2 \sqrt{2}$ .

B.

P Q = 3 \sqrt{2}

.

C.

P Q = 4 \sqrt{2}

.

D.

P Q = \sqrt{2}

.

Xem đáp án

Chọn A.

Ta có: P(1;-1), Q( -1;1). Do đó $P Q = \sqrt{{(- 1 - 1)}^{2} + {(1 + 1)}^{2}} = 2 \sqrt{2}$ .

Câu 31:

Phép quay tâm O(0;0) góc quay

90^{o}

biến đường tròn

(C) : x^{2} + y^{2} - 4 x + 1 = 0

thành đường tròn có phương trình là:

A.

x^{2} + {(y + 2)}^{2} = 3

.

B.

x^{2} + {(y - 2)}^{2} = 3

.

C.

x^{2} + {(y + 2)}^{2} = 9

.

D.

x^{2} + {(y + 2)}^{2} = 5

.

Xem đáp án

Chọn B

Câu 32:

Trong mặt phẳng toạ độ Oxy, cho hai điểm A(3;2), B(1;1) và đường thẳng d: x - 2y - 3 = 0. Viết phương trình đường thẳng d' là ảnh của d qua phép tịnh tiến theo $\vec{A B}$

A.

d^{'} : 2 x + y - 11 = 0

.

B.

d^{'} : x - 2 y - 3 = 0

.

C.

d^{'} : x - 2 y + 1 = 0

.

D.

d^{'} : x - 2 y = 0

.

Xem đáp án

Chọn B

Câu 33:

Hãy tìm khẳng định sai?

A Phép tịnh tiến là phép dời hình.

B. Phép đồng nhất là phép dời hình.

C. Phép quay là phép dời hình .

D. Phép vị tự là phép dời hình.

Xem đáp án

Chọn D

Phép vị tự tâm O tỉ số k $(k \neq 0)$ là phép dời hình khi k = 1.

Câu 34:

Phép vị tự tâm O tỉ số k $(k \neq 0)$ biến mỗi điểm M thành M'. Mệnh đề nào sau đây đúng?

A

\vec{O M} = \frac{1}{k} \vec{O M^{'}}

.

B.

\vec{O M} = k \vec{O M^{'}}

.

C.

\vec{O M} = - k \vec{O M^{'}}

.

D.

\vec{O M} = - \vec{O M^{'}}

.

Xem đáp án

Chọn A

Câu 35:

Trong mặt phẳng toạ độ Oxy cho hai đường thẳng song song a và a' lần lượt có phương trình $2 x - 3 y - 1 = 0$ và $2 x - 3 y + 5 = 0$ . Phép tịnh tiến nào sau đây không biến đường thẳng a thành đường thẳng a'

A. $\vec{u} = (0; 2)$ .

B.

\vec{u} = (- 3; 0)

.

C.

\vec{u} = (3; 4)

.

D.

\vec{u} = (- 2; 1)

.

Xem đáp án

Chọn D

Câu 36:

Trong mặt phẳng tọa độ Oxy, cho đường tròn $(C) : x^{2} + {(y - 2)}^{2} = 9$ ; $(C') : {(x - 1)}^{2} + {(y + 1)}^{2} = 16$ . Gọi (C') là ảnh của (C) qua phép đồng dạng tỉ số k, khi đó giá trị của k là:

A. $k = \frac{4}{3}$ .

B.

k = \frac{3}{4}

.

C.

k = \frac{9}{16}

.

D.

k = \frac{16}{9}

.

Xem đáp án

Chọn A.

Ta có: $k = \frac{R'}{R} = \frac{4}{3}$ .

Câu 37:

Trong mặt phẳng tọa độ Oxy,Tìm ảnh của điểm M(2;2) qua phép quay $Q (O; 45^{0})$

A. $M' (2; - 2 \sqrt{2})$ .

B.

M' (2 \sqrt{2}; 2)

.

C.

M' (0; 2 \sqrt{2})

.

D.

M' (2 \sqrt{2}; 0)

.

Xem đáp án

Chọn C.

Câu 38:

Cho hai đường tròn (O;R)và (O',R') tiếp xúc trong tại A $(R' < R)$ . Đường kính qua A cắt (O;R)tại B và cắt (O',R') tại C. Một đường thẳng di động qua A cắt (O;R) tại M và cắt (O',R') tại N. Gọi $I = B N \cap C M$ . Mệnh đề nào sau đây đúng?

A. Tập hợp điểm I là đường tròn $(O'') = V (M, \frac{R'}{R + R'}) ((O; R))$ .

B. Tập hợp điểm I là đường tròn

(O'') = V (M, \frac{R}{R + R'}) ((O; R))

.

C. Tập hợp điểm I là đường tròn

(O'') = V (C, \frac{R'}{R + R'}) ((O; R))

D. Tập hợp điểm I là đường tròn

(O'') = V (C, \frac{R}{R + R'}) ((O; R))

.

Xem đáp án

Chọn C.

Câu 39:

Trong mặt phẳng tọa độ Oxy, cho tam giác ABC vuông tại A và có $A (1; - 1); B (0; 1); C (- 5; - 4)$ . Gọi A'B'C' là ảnh của tam giác ABC qua phép vị tự tâm O, tỉ số $- \frac{3}{2}$ . Tính diện tích tam giác A'B'C'.

A. $\frac{45}{2}$ .

B.

\frac{135}{8}

.

C.

\frac{45}{4}

.

D.

\frac{135}{4}

.

Xem đáp án

Chọn B.

Câu 40:

Cho tam giác ABC. Dựng về phía ngoài tam giác đó các tam giác BAE và CAF vuông cân tại A Gọi I,M,J theo thứ tự là trung điểm của $E B; B C; C F$ . Khẳng định nào sau đây đúng ?

A. Tam giác IMJ là tam giác tù

B. Tam giác IMJ là tam giác vuông cân tại I.

C. Tam giác IMJ là tam giác đều.

D. Tam giác IMJ là tam giác vuông tại M.

Xem đáp án

Chọn D.

Câu 41:

Tìm tập xác định của hàm số sau

y = \frac{\cot x}{2 \sin x - 1}

.

Xem đáp án

Điều kiện xác định của hàm số là: $\{\begin{cases} 2 \sin x - 1 \neq 0 \\ \sin x \neq 0 \end{cases} \Leftrightarrow \{\begin{cases} x \neq \frac{π}{6} + k 2 π \\ x \neq \frac{5 π}{6} + k 2 π \\ x \neq k π \end{cases}$

Vậy tập xác định của hàm số là $D = ℝ \ \{\frac{π}{6} + k 2 π; \frac{5 π}{6} + k 2 π; k π, k \in ℤ\}$ .

Câu 42:

Giải phương trình

\sqrt{3} \sin 2 x - \cos 2 x + 1 = 0

Xem đáp án

Giải phương trình căn 3 sin2x - cos 2x + 1 =0 (ảnh 1)

Câu 43:

Trong mặt phẳng tọa độ Oxy, cho $\vec{v} = (1; - 3)$ , đường thẳng $(d) : 2 x - 3 y + 5 = 0$ và đường tròn $(C) : {(x - 2)}^{2} + {(y - 4)}^{2} = 4$ .

a. Viết phương trình đường thẳng d' là ảnh của d qua phép tịnh tiến $T_{\vec{v}}$ .

Xem đáp án

Trong mặt phẳng tọa độ Oxy , cho vecto v = (1;-3) , đường thẳng d: 2x - 3y + 5 = 0 và đường tròn (C): (x-2)^2 + ( y -4)^2 = 4 (ảnh 1)

Câu 44:

b. Viết phương trình đường tròn (C') là ảnh của (C) qua phép vị tự tâm O, tỉ số $k = \frac{1}{2}$ .

Xem đáp án

Bộ 20 đề thi giữa học kì 1 Toán 11 năm 2022 - 2023 có đáp án

Bộ 20 đề thi giữa học kì 1 Toán 11 năm 2022 - 2023 có đáp án (Đề 8)

Danh sách câu hỏi

Bài thi liên quan

Có thể bạn quan tâm

Các bài thi hot trong chương