39 câu hỏi trắc nghiệm thuộc Bộ 20 đề thi giữa học kì 1 Toán 11 năm 2022

Câu 1:

y = \tan (x - \frac{π}{4})

.

A. $D = \{x \in ℝ| x \neq \frac{π}{2} + k π, k \in ℤ\}$ .

B.

D = \{x \in ℝ| x \neq \frac{π}{4} + k π, k \in ℤ\}

.

C.

D = \{x \in ℝ| x \neq \frac{3 π}{2} + k π, k \in ℤ\}

.

D.

D = \{x \in ℝ| x \neq \frac{3 π}{4} + k π, k \in ℤ\}

.

Xem đáp án

Chọn D

Hàm số $y = \tan (x - \frac{π}{4})$ xác định $\Leftrightarrow \cos (x - \frac{π}{4}) \neq 0$

$\Leftrightarrow x - \frac{π}{4} \neq \frac{π}{2} + k π \Leftrightarrow x \neq \frac{3 π}{4} + k π$ .

Câu 2:

Tập giá trị của hàm số y = 4sin3x là

A. [-1;1]

B. [-2;2]

C. [-6;6]

D. [-4;4]

Xem đáp án

Chọn D

Ta có

$\begin{array}{l} - 1 \leq \sin 3 x \leq 1, \forall x \in ℝ \\ \Leftrightarrow - 4 \leq 4 \sin 3 x \leq 4, \forall x \in ℝ \end{array}$

$\Leftrightarrow - 4 \leq y \leq 4, \forall x \in ℝ$

Vậy tập giá trị của hàm số y = 4sin3x là [-4;4].

Câu 3:

Trong các hàm số sau, hàm số nào là hàm số chẵn?

A. $y = \sin |2020 x| + \cos 2021 x$ .

B.

y = \cos |2020 x| + \sin 2021 x

.

C.

y = \cot 2020 x - 2021 \sin x

.

D.

y = \tan 2021 x + \cot 2020 x

.

Xem đáp án

Chọn A

Câu 4:

Hàm số y = sinx đồng biến trên mỗi khoảng nào trong các mỗi khoảng sau?

A. $(- \frac{π}{2} + k 2 π; \frac{π}{2} + k 2 π)$ với $k \in ℤ$ .

B.

(- \frac{3 π}{2} + k 2 π; \frac{5 π}{2} + k 2 π)

với

k \in ℤ

.

C.

(\frac{π}{2} + k 2 π; \frac{5 π}{2} + k 2 π)

với

k \in ℤ

.

D.

(\frac{π}{2} + k 2 π; π + k 2 π)

với

k \in ℤ

.

Xem đáp án

Chọn A

Câu 5:

Nghiệm của phương trình

\sin x = - \frac{1}{2}

là

A. $[\begin{array}{l} x = \frac{π}{6} + k 2 π \\ x = \frac{7 π}{6} + k 2 π \end{array} (k \in ℤ)$ .

B.

[\begin{array}{l} x = - \frac{π}{6} + k 2 π \\ x = \frac{5 π}{6} + k 2 π \end{array} (k \in ℤ)

.

C.

[\begin{array}{l} x = - \frac{π}{6} + k 2 π \\ x = \frac{7 π}{6} + k 2 π \end{array} (k \in ℤ)

.

D.

[\begin{array}{l} x = - \frac{π}{6} + k 2 π \\ x = - \frac{7 π}{6} + k 2 π \end{array} (k \in ℤ)

.

Xem đáp án

Chọn C

Ta có:

$\sin x = - \frac{1}{2} \Leftrightarrow \sin x = \sin (- \frac{π}{6}) \Leftrightarrow [\begin{array}{l} x = - \frac{π}{6} + k 2 π \\ x = \frac{7 π}{6} + k 2 π \end{array} (k \in ℤ) .$

Câu 6:

Tập nghiệm của phương trình tanx + 1 = 0 là

A. $S = \{- \frac{π}{4} + k 2 π, k \in ℤ\}$ .

B.

S = \{\frac{π}{4} + k π, k \in ℤ\}

.

C.

S = \{- \frac{π}{4} + k π, k \in ℤ\}

.

D.

S = \{\frac{π}{4} + k 2 π, k \in ℤ\}

.

Xem đáp án

Chọn C

Câu 7:

Tập nghiệm của phương trình $3 c o s (3 x - \frac{π}{3}) = 0$ là

A. $\{\frac{π}{2} + k π, k \in ℤ\}$ .

B.

\{\frac{5 π}{18} + \frac{k π}{3}, k \in ℤ\}

.

C.

\{\frac{5 π}{6} + k 2 π, k \in ℤ\}

.

D.

\{\frac{5 π}{18} + \frac{k 2 π}{3}, k \in ℤ\}

.

Xem đáp án

Chọn B

Ta có: $3 c o s (3 x - \frac{π}{3}) = 0 \Leftrightarrow c o s (3 x - \frac{π}{3}) = 0 \Leftrightarrow 3 x - \frac{π}{3} = \frac{π}{2} + k π \Leftrightarrow x = \frac{5 π}{18} + \frac{k π}{3} .$ .

Câu 8:

Số nghiệm của phương trình sin2x = 0 thỏa mãn

0 < x < 2 π

là?

A. 2

B. 1

C. 3

D. 0

Xem đáp án

Chọn C

$\sin 2 x = 0 \Leftrightarrow 2 x = k π; k \in ℤ \Leftrightarrow x = k \frac{π}{2}; k \in ℤ$ .

Do $0 < x < 2 π \Rightarrow 0 < k \frac{π}{2} < 2 π \Rightarrow 0 < k < 4 \overset{k \in Z}{\to} k = \{1; 2; 3\}$ .

Câu 9:

Phương trình nào trong các phương trình sau có nghiệm ?

A. $\sin x + \cos x + 3 = 0$ .

B.

\sin x - \cos x = 2

.

C.

2 \sin x - 3 \cos x = 1

.

D.

\sin x + 3 \cos x = 6

.

Xem đáp án

Chọn C

Vì $2 \sin x - 3 \cos x = 1$ có $a^{2} + b^{2} = 13 > 1 = c^{2} .$

Câu 10:

Lớp 12A có 18 học sinh nữ và 17 học sinh nam. Giáo viên chọn 1 học sinh trong lớp làm tình nguyện viên tham gia phong trào thanh niên của nhà trường. Hỏi có bao nhiêu cách chọn?

A. 306

B. 1

C. 35

D. 17

Xem đáp án

Chọn C

Tổng số học sinh của lớp là 18 + 17=35.

Số cách chọn 1 học sinh trong lớp là 35 cách.

Câu 11:

Có bao nhiêu cách chọn 2 số tự nhiên nhỏ hơn 7 , trong đó có 1 số lẻ và 1 số chẵn?

A. 20

B. 12

C. 9

D. 6

Xem đáp án

Chọn B

Tập các số tự nhiên nhỏ hơn 7 là $\{0,1,2,3,4,5,6\}$

Chọn 1 số lẻ trong 3 sốlẻ: có 3 cách

Chọn 1 số chẵn trong 4 số chẵn: Có 4 cách

Áp dụng quy tắc nhân, có 3.4 =12 cách.

Câu 12:

Cho A là tập hợp gồm 20 điểm phân biệt. Số đoạn thẳng có hai đầu mút phân biệt thuộc tập A là

A. 170

B. 160

C. 190

D. 360

Xem đáp án

Chọn C

Chọn ngẫu nhiên 2 điểm phân biệt sẽ tạo thành một đoạn thẳng.

Do đó số đoạn thẳng là $C_{20}^{2} = 190.$

Câu 13:

Số cách chọn ngẫu nhiên 1 học sinh làm lớp trưởng, 1học sinh làm bí thư từ tập thể lớp gồm 35 học sinh là

A. $A_{35}^{2}$ .

B.

C_{2}^{35}

.

C.

A_{2}^{35}

.

D.

C_{35}^{2}

.

Xem đáp án

Chọn A

Mỗi cách chọn hai học sinh vào hai chức danh lớp trưởng và bí thư là một chỉnh hợp chập 2 của 35 phần tử.

Do đó, số cách chọn ngẫu nhiên 1học sinh làm lớp trưởng, 1 học sinh làm bí thư từ tập thể lớp gồm 35 học sinh là $A_{35}^{2}$ .

Câu 14:

Có bao nhiêu cách sắp xếp 7 bạn học sinh thành một hàng ngang?

A. $P_{7}$ .

B.

C_{7}^{7}

.

C.

C_{7}^{1}

.

D.

A_{7}^{1}

.

Xem đáp án

Chọn A

Mỗi cách xếp 7 học sinh thành một hàng ngang là một hoán vị của 7 phần tử và ngược lại.

Vậy số cách xếp là $P_{7}$ .

Câu 15:

Ảnh của điểm M(0;1) qua phép tịnh tiến theo vectơ

\vec{u} = (1; 2)

là điểm nào?

A. $M^{'} (2; 3)$ .

B.

M^{'} (1; 3)

.

C.

M^{'} (1; 1)

.

D.

M^{'} (- 1; -1)

.

Xem đáp án

Chọn B

Ta có: $T_{\vec{u}} (M) = M^{'} \Leftrightarrow \vec{M M^{'}} = \vec{u}$ . $\to M^{'} = (1; 3)$

Câu 16:

Cho hình vuông ABCD tâm I. Ta có

A. $T_{\vec{A I}} (I) = B$ .

B.

T_{\vec{A I}} (I) = D

.

C.

T_{\vec{A I}} (I) = C

.

D.

T_{\vec{A I}} (I) = A

.

Xem đáp án

Chọn C

Câu 17:

Trong mặt phẳng tọa độ Oxy, Qua phép quay tâm O, góc quay

90 °

biến điểm M(-3;5) thành điểm nào?

A. (3;4)

B. (-5;-3)

C. (5;-3)

D. (-3;-5)

Xem đáp án

Đáp án B

Câu 18:

Giả sử

. Khi đó mệnh đề nào sau đây sai?

A. Giả sử Q( O, gama) (M) M',Q( O, gama) (N) (N'). Khi đó mệnh đề nào sau đây sai? (ảnh 2)

B.

Giả sử Q( O, gama) (M) M',Q( O, gama) (N) (N'). Khi đó mệnh đề nào sau đây sai? (ảnh 3)

C. MN = M'N'.

D.

Giả sử Q( O, gama) (M) M',Q( O, gama) (N) (N'). Khi đó mệnh đề nào sau đây sai? (ảnh 4)

Xem đáp án

Đáp án A.

Câu 19:

Cho hai đường thẳng cắt nhau d và d'. Có bao nhiêu phép vị tự biến d thành đường thằng d'?

A. 0

B. 1

C. 2

D. Vô số

Xem đáp án

Chọn B

Vì qua phép vị tự, đường thẳng biến thành đường thẳng song song hoặc trùng với nó.

Câu 20:

Tập xác định của hàm số

y = \frac{\tan x}{\cos x + 1}

là

A. $ℝ \ \{π + k 2 π, k \in ℤ\}$ .

B.

ℝ \ \{\frac{π}{2} + k π; k 2 π, k \in ℤ\}

.

C.

ℝ \ \{\frac{π}{2} + k π; π + k 2 π, k \in ℤ\}

.

D.

ℝ \ \{\frac{k π}{2}, k \in ℤ\}

.

Xem đáp án

Chọn C

Điều kiện xác định: $\{\begin{cases} \cos x \neq 0 \\ \cos x \neq - 1 \end{cases} \Leftrightarrow \{\begin{cases} x \neq \frac{π}{2} + k π \\ x \neq π + k 2 π \end{cases}, (k \in ℤ)$ .

Câu 21:

Phương trình mcosx - 1= 0 có nghiệm khi m thỏa mãn điều kiện

A. $\{\begin{cases} m \geq - 1 \\ m \leq 1 \end{cases}$ .

B.

[\begin{array}{l} m \leq - 1 \\ m \geq 1 \end{array}

.

C.

m \geq - 1

D.

m \geq 1

.

Xem đáp án

Chọn B

Câu 22:

Cho phương trình $2 \sin x - \sqrt{3} = 0$ . Tổng các nghiệm thuộc đoạn $[0; π]$ của phương trình là

A.

π

B.

\frac{π}{3} .

C.

\frac{2 π}{3} .

D.

\frac{4 π}{3} .

Xem đáp án

Chọn A

Câu 23:

Nghiệm của phương trình tanx + cotx = 2 là

A. $- \frac{π}{4} + k π$ .

B.

\frac{π}{4} + k π

.

C.

\frac{5 π}{4} + k 2 π

.

D.

- \frac{3 π}{4} + k 2 π

.

Xem đáp án

Chọn B

Câu 24:

Tất cả các nghiệm của phương trình cos2x + sinx + 2 = 0 là

A. $[\begin{array}{l} x = - \frac{π}{2} + k 2 π \\ x = \arcsin (\frac{2}{3}) + k 2 π \end{array} (k \in ℤ)$ .

B.

x = - \frac{π}{2} + k 2 π (k \in ℤ)

.

C.

[\begin{array}{l} x = - \frac{π}{2} + k 2 π \\ x = \arcsin (\frac{3}{2}) + k 2 π \end{array} (k \in ℤ)

.

D.

x = \frac{π}{2} + k 2 π (k \in ℤ)

.

Xem đáp án

Chọn B

Câu 25:

Từ các chữ số 0,1,2,3,4,5 có thể lập được bao nhiêu số tự nhiên có sáu chữ số khác nhau?

A. 600

B. 240

C. 720

D. 625

Xem đáp án

Chọn A

Câu 26:

Có 10 cặp vợ chồng đi dự tiệc. Tổng số cách chọn một người đàn ông và một người đàn bà trong bữa tiệc phát biểu ý kiến sao cho hai người đó không là vợ chồng.

A. 100

B. 90

C. 20

D. 19

Xem đáp án

Chọn B

Chọn 1 người đàn ông phát biểu có 10 cách.

Chọn 1 người đàn bà phát biểu có 10 cách.

Số cách chọn một người đàn ông và một người đàn bà trong bữa tiệc phát biểu ý kiến sao cho hai người đó không là vợ chồng là $10.10 - 10 = 90$ .

Câu 27:

Số đường chéo của đa giác đều có 20 cạnh là bao nhiêu?

A. 170

B. 190

C. 360

D. 380

Xem đáp án

Chọn A

Số đường chéo của đa giác đều là: $C_{20}^{2} - 20 = 170$ .

Câu 28:

Nhân dịp lễ sơ kết học kì I, để thưởng cho ba học sinh có thành tích tốt nhất lớp, cô An đã mua 10 cuốn sách khác nhau và chọn ngẫu nhiên 3 cuốn để phát thưởng cho 3 học sinh đó mỗi học sinh nhận 1 cuốn. Hỏi cô An có bao nhiêu cách phát thưởng?

A.

C_{10}^{3}

.

B.

A_{10}^{3}

.

C.

10^{3}

.

D.

3 C_{10}^{3}

.

Xem đáp án

Chọn B

Số cách chọn 3 cuốn sách để phát thưởng cho 3 học sinh là cách chọn 3 phần tử khác nhau trong 10 phần tử có phân biệt thứ tự, nên số cách chọn thỏa mãn yêu cầu là $A_{10}^{3}$ .

Vậy cô An có $A_{10}^{3}$ cách phát thưởng.

Câu 29:

Một nhóm học sinh gồm 4 học sinh nam và 5 học sinh nữ. Hỏi có bao nhiêu cách sắp xếp 9 học sinh trên thành 1 hàng dọc sao cho nam nữ đứng xen kẽ?

A. 5760

B. 2880

C. 120

D. 362880

Xem đáp án

Chọn B

Xếp 4 học sinh nam thành hàng dọc có $4!$ cách xếp.

Giữa 4 học sinh nam có 5 khoảng trống ta xếp các bạn nữ vào vị trí đó nên có $5!$ cách xếp.

Theo quy tắc nhân có $4! 5! = 2880$ cách xếp thoả mãn bài ra.

Câu 30:

Từ 20 bông hoa gồm có 8 bông màu đỏ, 7 bông màu vàng, 5 bông màu trắng; chọn ngẫu nhiên 4 bông để tạo thành một bó. Có bao nhiêu cách chọn để bó hoa có đủ cả ba màu?

A. 14280

B. 4760

C. 2381

D. 2380

Xem đáp án

Chọn D

Để chọn ra 4 bông có đủ 3 màu, ta có thể chọn:

2 bông đỏ, 1 bông vàng, 1 bông trắng.

1 bông đỏ, 2 bông vàng, 1 bông trắng.

1 bông đỏ, 1 bông vàng, 2 bông trắng.

Vậy số cách chọn là $C_{8}^{2} . C_{7}^{1} . C_{5}^{1} + C_{8}^{1} . C_{7}^{2} . C_{5}^{1} + C_{8}^{1} . C_{7}^{1} . C_{5}^{2} = 2380.$

Câu 31:

Cho

\vec{v} = (3; 3)

và đường tròn

(C) : x^{2} + y^{2} - 2 x + 4 y - 4 = 0

. Ảnh của (C) qua phép tịnh tiến theo véctơ

\vec{v}

là (C') có phương trình là

A. ${(x - 4)}^{2} + {(y - 1)}^{2} = 9$ .

B.

{(x + 4)}^{2} + {(y + 1)}^{2} = 9

.

C.

x^{2} + y^{2} + 8 x + 2 y - 4 = 0

.

D.

{(x - 4)}^{2} + {(y - 1)}^{2} = 4

.

Xem đáp án

Chọn A

Câu 32:

Trong mặt phẳng tọa độ Oxy, cho điểm M'(-4;2) , biết M' là ảnh của M qua phép tịnh tiến theo véctơ v = (1;-5). Tìm tọa độ điểm M.

A. M(-3;5).

B. M(3;7).

C. M(-5;7).

D. M(-5;-3).

Xem đáp án

Đáp án C.

Câu 33:

Trong mặt phẳng tọa độ Oxy, cho hai điểm A(-5;2), C(-1;0). Biết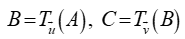. Tìm tọa độ của vectơ u + v để có thể thực hiện phép tịnh tiến T u + v biến điểm A thành điểm C

A. (-6;2)

B. (2;-4)

C. (4;-2)

D. (4;2)

Xem đáp án

Đáp án C.

Câu 34:

Cho lục giác đều ABCDEF tâm O như hình bên. Tam giác EOD là ảnh của tam giác AOF qua phép quay tâm O góc quay $α$ . Tìm $α$ biết $- 180 ° < α < 180 °$ .

A. $α = 60^{o}$ .

B.

α = - 60^{o}

.

C.

α = 120^{o}

.

D.

α = - 120^{o}

.

Xem đáp án

Chọn C

Câu 35:

Cho $∆ A B C$ có trọng tâm G. Gọi M,N,P lần lượt là trung điểm của các cạnh AB,BC,CA. Phép vị tự nào sau đây biến $∆ A B C$ thành $∆ N P M$ ?

A. Cho tam giác ABC có trọng tâm G . Gọi M,N,P lần lượt là trung điểm của các cạnh AB,BC,CA . Phép vị tự nào sau đây biến (ảnh 1)

B. Cho tam giác ABC có trọng tâm G . Gọi M,N,P lần lượt là trung điểm của các cạnh AB,BC,CA . Phép vị tự nào sau đây biến (ảnh 2)

C. Cho tam giác ABC có trọng tâm G . Gọi M,N,P lần lượt là trung điểm của các cạnh AB,BC,CA . Phép vị tự nào sau đây biến (ảnh 3)

D. Cho tam giác ABC có trọng tâm G . Gọi M,N,P lần lượt là trung điểm của các cạnh AB,BC,CA . Phép vị tự nào sau đây biến (ảnh 4)

Xem đáp án

Đáp án D.

Câu 36:

Giải phương trình sau $\frac{\cos x - \sqrt{3} \sin x}{2 \sin x - 1} = 0$ .

Xem đáp án

Điều kiện: $2 \sin x - 1 \neq 0 \Leftrightarrow \sin x \neq \frac{1}{2} \Leftrightarrow \{\begin{cases} x \neq \frac{π}{6} + k 2 π \\ x \neq \frac{5 π}{6} + k 2 π \end{cases} (k \in ℤ) (1)$ .

Ta có $\frac{\cos x - \sqrt{3} \sin x}{2 \sin x - 1} = 0 \Leftrightarrow \cos x - \sqrt{3} \sin x = 0 \Leftrightarrow \frac{1}{2} \cos x - \frac{\sqrt{3}}{2} \sin x = 0$

$\Leftrightarrow \cos x \cos \frac{π}{3} - \sin x . \sin \frac{π}{3} = 0 \Leftrightarrow \cos (x + \frac{π}{3}) = 0 \Leftrightarrow x + \frac{π}{3} = \frac{π}{2} + k π \Leftrightarrow x = \frac{π}{6} + k π, k \in ℤ$ .

Kết hợp với điều kiện (1), nghiệm của phương trình là $x = - \frac{5 π}{6} + k 2 π, k \in ℤ$ .

Câu 37:

Trong mặt phẳng Oxy, cho đường thẳng d: $x + 2 y - 3 = 0$ . Phép đồng dạng có được bằng cách thực hiện liên tiếp phép vị tự tâm O tỉ số k = 2 và phép tịnh tiến theo vectơ $\vec{v} = (1; 2)$ biến đường thẳng d thành đường thẳng d' . Viết phương trình đường thẳng d'.

Xem đáp án

Trong mặt phẳng Oxy, cho đường thẳng d : x + 2y - 3 = 0. Phép đồng dạng có được bằng cách thực hiện liên tiếp phép vị tự tâm O (ảnh 1)

Câu 38:

Có bao nhiêu số tự nhiên gồm 5 chữ số phân biệt sao cho 1, 2, 3 luôn đứng cạnh nhau.

Xem đáp án

Có bao nhiêu số tự nhiên gồm 5 chữ số phân biệt sao cho 1, 2, 3 luôn đứng cạnh nhau. (ảnh 1)

Câu 39:

Có hai học sinh lớp A ba học sinh lớp B và bốn học sinh lớp C xếp thành một hàng ngang sao cho giữa hai học sinh lớp A không có học sinh nào lớp B Hỏi có bao nhiêu cách xếp hàng như vậy ?

Xem đáp án

Bộ 20 đề thi giữa học kì 1 Toán 11 năm 2022 - 2023 có đáp án

Bộ 20 đề thi giữa học kì 1 Toán 11 năm 2022 - 2023 có đáp án (Đề 15)

Danh sách câu hỏi

Bài thi liên quan

Có thể bạn quan tâm

Các bài thi hot trong chương