10 câu hỏi trắc nghiệm thuộc Dạng 4: Tính độ dài của tổng và hiệu hai hay nhiều vectơ có đáp án

Câu 1:

Cho hình vuông ABCD tâm I, có cạnh bằng a. Tính $|\vec{A B} + \vec{A D}|$ .

A.

a \sqrt{2}

;

B. a;

C. 2a;

D.

\frac{a}{2}

.

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: A.

Cho hình vuông ABCD tâm I, có cạnh bằng a. Tính | AB+AD|. (ảnh 1)

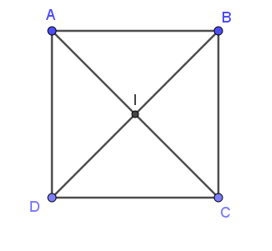
Áp dụng quy tắc hình bình hành, ta có: $\vec{A B} + \vec{A D} = \vec{A C} \Rightarrow |\vec{A B} + \vec{A D}| = |\vec{A C}| = A C$ .

Xét tam giác ADC vuông tại D (do ABCD là hình vuông) có:

Áp dụng định lý Pythagore cho tam giác vuông ACD, ta có:

AC² = AD² + CD² = a² + a² = 2a² ⇔ AC = $a \sqrt{2}$

Vậy $|\vec{A B} + \vec{A D}| = a \sqrt{2}$ .

Câu 2:

Cho tam giác ABC vuông cân tại A có AB = a. Độ dài của vectơ $\vec{a} = \vec{A B} + \vec{A C}$ là:

A.

a \sqrt{2}

;

B.

\frac{a \sqrt{2}}{2}

;

C. 2a;

D. a

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: A.

Cho tam giác ABC vuông cân tại A có AB = a. Độ dài của vectơ a= vecto AB+AC là: (ảnh 1)

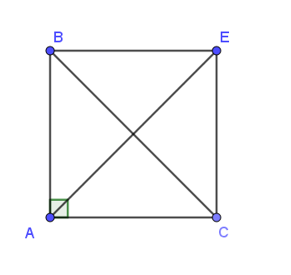
Vẽ hình bình hành ABEC, theo quy tắc hình bình hành, ta có: $\vec{A B} + \vec{A C} = \vec{A E}$ .

Do ABC là tam giác vuông cân cạnh AB = a nên ABEC là hình vuông cạnh a.

Xét tam giác ABE vuông tại B

Áp dụng định lý Pythagore ta có:

AE² = AB² + BE² = a² + a² = 2a² ⇔ AE = $a \sqrt{2}$

Vậy $|\vec{a}| = |\vec{A B} + \vec{A C}| = a \sqrt{2}$ .

Câu 3:

Cho tam giác ABC vuông cân tại C và AB = $\sqrt{2}$ . Tính $|\vec{A B} - \vec{A C}|$ .

A. 3

B. 1

C. 2

D. 4

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: B.

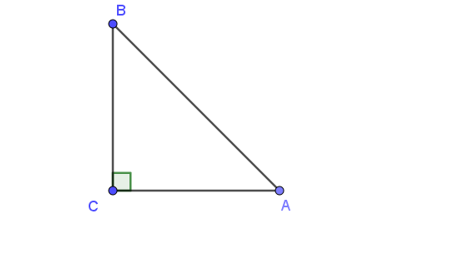
Cho tam giác ABC vuông cân tại C và AB = căn bậc hai 2. Tính | vecto AB-AC|. (ảnh 1)

Ta có: $\vec{A B} - \vec{A C} = \vec{C B} \Rightarrow |\vec{A B} - \vec{A C}| = |\vec{C B}| = C B$ .

Xét tam giác ABC vuông tại C

Áp dụng định lý Pythagore ta có:

AB² = BC² + CA²

Mà BC = CA nên BC² = CA² = $\frac{A B^{2}}{2}$ = $\frac{{(\sqrt{2})}^{2}}{2}$ =1

⇔ CB = CA = 1

Vậy $|\vec{A B} - \vec{A C}|$ = 1.

Câu 4:

Cho tam giác ABC vuông tại A có AB = 3, AC = 4. Độ dài của vectơ $\vec{u} = \vec{C A} + \vec{A B}$ bằng:

A. 2

B.

2 \sqrt{13}

;

C. 5

D.

\sqrt{13}

.

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: C.

Cho tam giác ABC vuông tại A có AB = 3, AC = 4. Độ dài của vectơ u=vecto CA+AB bằng: (ảnh 1)

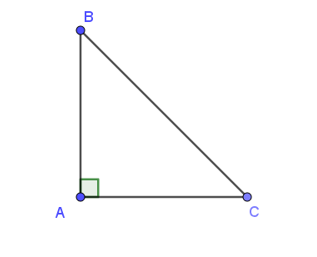
Xét tam giác ABC vuông tại A

Áp dụng định lý Pythagore ta có:

BC² = AB² + AC² = 4² + 3² = 25 ⇔ BC = 5

Ta có: $\vec{C A} + \vec{A B} = \vec{C B} \Rightarrow |\vec{C A} + \vec{A B}| = |\vec{C B}| = C B = 5$ .

Vậy $|\vec{u}| = 5$ .

Câu 5:

Cho tam giác ABC có: AB = AC = a và $\hat{B A C} = 120 °$ . Ta có $|\vec{A B} + \vec{A C}|$ = ?

A.

a \sqrt{3}

;

B. a;

C.

\frac{a}{2}

;

D. 2a.

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: B.

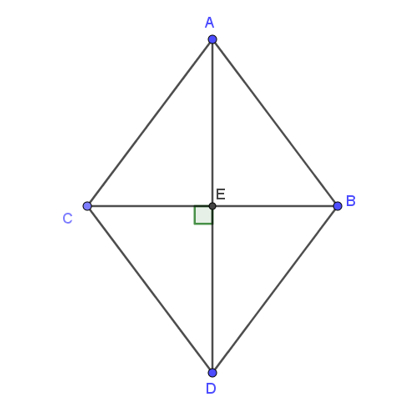
Cho tam giác ABC có: AB = AC = a và góc BAC=120 độ. Ta có | vecto AB+AC| = ? (ảnh 1)

Dựng hình bình hành ABDC.

Do tam giác ABC cân có: AB = AC = a nên ABDC là hình thoi cạnh a.

Gọi E là giao điểm hai đường chéo AD và BC của hình thoi.

Có $\hat{B A C} = 120 ° \Rightarrow \hat{C A E} = 60 °$ (đường chéo của hình thoi cũng là tia phân giác của các góc ở đỉnh).

Xét tam giác AEC vuông tại E (do trong hình thoi, hai đường chéo vuông góc với nhau) có:

$\cos \hat{C A E} = \frac{A E}{A C} \Rightarrow A E = A C . \cos \hat{C A E} = a . c o s 60 ° = \frac{a}{2}$ .

Lại có: AD = 2AE = $2. \frac{a}{2} = a$ .

Theo quy tắc hình bình hành ta có: $\vec{A B} + \vec{A C} = \vec{A D} \Rightarrow |\vec{A B} + \vec{A C}| = |\vec{A D}| = A D = a$ .

Câu 6:

Cho tam giác ABC đều cạnh a, H là trung điểm của BC. Tính $|\vec{C A} - \vec{H C}|$ .

A. $\frac{a}{2}$

B. $\frac{3 a}{2}$

C. $\frac{2 \sqrt{3} a}{3}$

D. $\frac{a \sqrt{7}}{2}$

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: D.

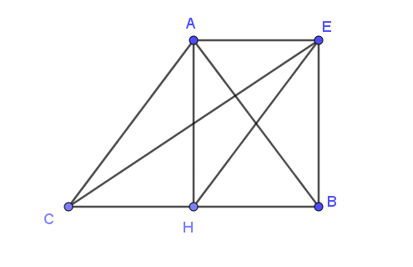
Cho tam giác ABC đều cạnh a, H là trung điểm của BC. Tính | vecto CA- vecto HC| . (ảnh 1)

Ta có: $\vec{C A} - \vec{H C} = \vec{C A} + \vec{C H}$

Dựng hình bình hành CAEH.

Do tam giác ABC đều nên AH vừa là trung tuyến vừa là đường cao.

Do đó, AH vuông góc với BC $\Rightarrow \hat{A H B} = 90 °$ .

Mà AE // CH (do CAEH là hình bình hành)

Do đó, AH vuông góc với AE $\Rightarrow \hat{H A E} = 90 °$ .

Vậy AEBH là hình chữ nhật.

Ta có: CH = BH = $\frac{B C}{2} = \frac{a}{2}$ .

Xét tam giác CHA vuông tại H

Áp dụng định lý Pythagore ta có:

AC² = AH² + CH² ⇔ AH² = AC² – CH² = $a^{2} - {(\frac{a}{2})}^{2} = \frac{3 a^{2}}{4}$ ⇒ $A H = \frac{a \sqrt{3}}{2}$ .

⇒ $E B = A H = \frac{a \sqrt{3}}{2}$ (do AEBH là hình chữ nhật)

Xét tam giác CBE vuông tại B

Áp dụng định lý Pythagore ta có:

CE² = BC² + BE²= $a^{2} + {(\frac{a \sqrt{3}}{2})}^{2} = \frac{7}{4} a^{2}$ ⇒ $C E = \frac{a \sqrt{7}}{2}$ .

Theo quy tắc hình bình hành: $\vec{C A} + \vec{C H} = \vec{C E}$ .

$\Rightarrow |\vec{C A} - \vec{H C}| = |\vec{C A} + \vec{C H}| = |\vec{C E}| = C E = \frac{a \sqrt{7}}{2}$ .

Câu 7:

Độ dài của vectơ $\vec{x} = \vec{I A} - \vec{I B}$ với I là trung điểm của đoạn thẳng AB = 4 là:

A. 2

B. 4

C. 3

D. 6

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: B

Ta có: $\vec{I A} - \vec{I B} = \vec{I A} + \vec{B I} = \vec{B I} + \vec{I A} = \vec{B A}$

$\Rightarrow |\vec{I A} - \vec{I B}| = |\vec{B A}| = A B = 4$ .

Vậy $|\vec{x}| = 4$ .

Câu 8:

Cho hình vuông ABCD cạnh 2a. Tính $|\vec{A B} - \vec{D A}|$ .

A.

a \sqrt{2}

;

B. a;

C.

2 a \sqrt{2}

;

D. 2a.

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: C.

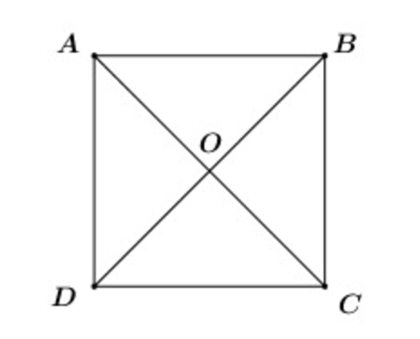
Cho hình vuông ABCD cạnh 2a. Tính | vecto AB- vecto DA| (ảnh 1)

Ta có: $\vec{A B} - \vec{D A} = \vec{A B} + \vec{A D} = \vec{A C}$ (áp dụng quy tắc hình bình hành cho hình vuông ABCD).

Xét tam giác ADC vuông tại D

Áp dụng định lý Pythagore ta có:

AC² = AD² + DC² = (2a)² + (2a)² = 8a² ⇒ AC = $2 a \sqrt{2}$

Vậy $|\vec{A B} - \vec{D A}| = 2 a \sqrt{2}$ .

Câu 9:

Cho hình vuông ABCD cạnh bằng 2, có tâm O. Khi đó ta tính được $|\vec{B O} - \vec{B C}| = a \sqrt{2} .$ Tính giá trị biểu thức A = 2a² – 5a.

A. 2;

B.

2 \sqrt{2}

;

C. – 3;

D. 0

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: C.

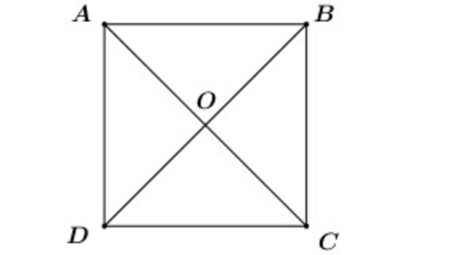
Cho hình vuông ABCD cạnh bằng 2, có tâm O. Khi đó ta tính được | vecto BO- veco BC| = a căn bậc hai 2 (ảnh 1)

Ta có: $\vec{B O} - \vec{B C} = \vec{C O}$ .

Xét tam giác ADC vuông tại D

Áp dụng định lý Pythagore ta có:

AC² = AD² + DC² = 2² + 2² = 8 ⇒ AC = $2 \sqrt{2}$

Do ABCD là hình vuông nên ta có: OA = OB = OC = OD = $\frac{A C}{2} = \frac{2 \sqrt{2}}{2} = \sqrt{2}$

$\Rightarrow |\vec{B O} - \vec{B C}| = |\vec{C O}| = C O = \sqrt{2}$ .

Theo bài ra ta có $|\vec{B O} - \vec{B C}| = a \sqrt{2} .$

Do đó, $a \sqrt{2} = \sqrt{2} \Leftrightarrow a = 1$ .

Vậy A = 2a² – 5a = 2 . 1² – 5 . 1 = 2 – 5 = – 3.

Câu 10:

Cho hình vuông ABCD cạnh 2, tâm O. Tính độ dài của vectơ $\vec{y}$ với $\vec{y} = \vec{B O} - \vec{B C} + \vec{O C}$ . Khẳng định nào sau đây là đúng?

A. $|\vec{y}|$ = 2;

B.

|\vec{y}|

=

2 \sqrt{2}

;

C.

|\vec{y}|

=

\sqrt{2}

;

D.

|\vec{y}|

= 0.

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: D.

Cho hình vuông ABCD cạnh 2, tâm O. Tính độ dài của vectơ y với (ảnh 1)

Ta có: $\vec{B O} - \vec{B C} + \vec{O C} = \vec{B O} + \vec{C B} + \vec{O C} = \vec{B O} + (\vec{O C} + \vec{C B}) = \vec{B O} + \vec{O B} = \vec{0}$ .

Do đó, $|\vec{B O} - \vec{B C} + \vec{O C}|$ = 0.

Vậy $|\vec{y}|$ = 0.

Trắc nghiệm Toán 10 CTST Bài 2: Tìm tổng của hai hay nhiều vectơ có đáp án

Dạng 4: Tính độ dài của tổng và hiệu hai hay nhiều vectơ có đáp án

Danh sách câu hỏi

Bài thi liên quan

Có thể bạn quan tâm

Các bài thi hot trong chương