10 câu hỏi trắc nghiệm thuộc Dạng 1: Xác định góc giữa hai vectơ có đáp án

Trắc nghiệm Toán 10 CTST Bài 4. Tích vô hướng của hai vectơ có đáp án

Dạng 1: Xác định góc giữa hai vectơ có đáp án

680 lượt thi
10 câu hỏi
0 phút

BẮT ĐẦU LÀM BÀI

Danh sách câu hỏi

Câu 1:

Cho tam giác ABC vuông cân tại A. Tính góc giữa hai vectơ $\vec{C A}$ và $\vec{B C}$ .

A. 45°;

B. 135°;

C. 90°;

D. 120°.

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: B.

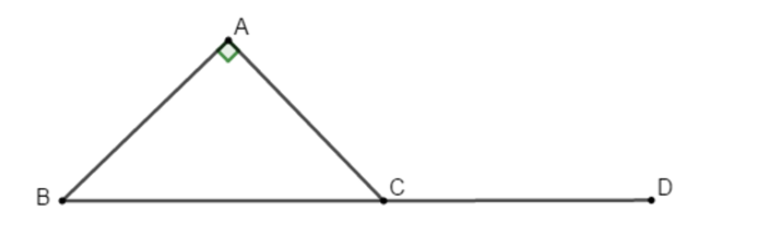
Cho tam giác ABC vuông cân tại A. Tính góc giữa hai vectơ CA và vecto BC. (ảnh 1)

Trên tia đối của CB lấy D sao cho CB = CD

Ta có: $\vec{C D} = \vec{B C}$

Khi đó: $(\vec{C A}, \vec{B C}) = (\vec{C A}, \vec{C D}) = \hat{A C D}$

Do tam giác ABC vuông cân tại A nên $\hat{A C B} = 45 °$ .

Ta có: $\hat{A C D} + \hat{A C B} = 180 °$ (hai góc kề bù)

$\Rightarrow \hat{A C D} = 180 ° - \hat{A C B} = 180 ° - 45 ° = 135 °$

Vậy $(\vec{C A}, \vec{B C}) = 135 °$ .

Câu 2:

Cho tam giác ABC đều. Tính góc $(\vec{A B}, \vec{A C})$ .

A. 90°;

B. 135°;

C. 90°;

D. 60°.

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: D.

Xét tam giác ABC đều có: $\hat{B A C} = 60 °$

$\Rightarrow (\vec{A B}, \vec{A C}) = \hat{B A C} = 60 °$ .

Câu 3:

Cho tam giác ABC vuông tại A có: AB = 4, BC = 8. Tính $(\vec{C B}, \vec{C A})$ .

A. 90°;

B. 60°;

C. 30°;

D. 45°.

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: C.

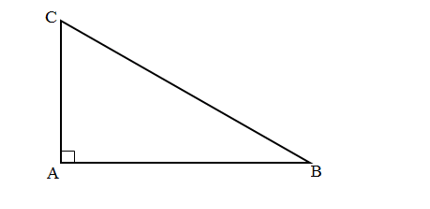
Cho tam giác ABC vuông tại A có: AB = 4, BC = 8. Tính ( vecto CB, vecto CA) (ảnh 1)

Xét tam giác ABC vuông tại A có:

$\sin \hat{A C B} = \frac{A B}{B C} = \frac{4}{8} = \frac{1}{2} \Rightarrow \hat{A C B} = 30 °$

Vậy

(\vec{C B}, \vec{C A}) = \hat{A C B} = 30 °

Câu 4:

Cho tam giác ABC vuông tại B. Có AB = 3, AC = 6. Tính $(\vec{A B}, \vec{A C})$ .

A. 90°;

B. 60°;

C. 30°;

D. 45°.

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: B.

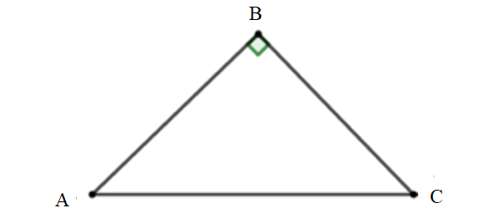
Cho tam giác ABC vuông tại B. Có AB = 3, AC = 6. Tính (vecto AB, vecto AC) (ảnh 1)

Xét tam giác ABC vuông tại A có:

$c o s \hat{B A C} = \frac{A B}{A C} = \frac{3}{6} = \frac{1}{2} \Rightarrow \hat{C A B} = 60 °$

Vậy $(\vec{A B}, \vec{A C}) = \hat{C A B} = 60 °$ .

Câu 5:

Cho tam giác ABC có AB = 5, AC = 6, BC = 4. Tính côsin của góc $(\vec{B A}, \vec{B C})$ .

A. $\frac{1}{8}$

B. $\frac{3}{8}$

C. $\frac{7}{8}$

D. $\frac{1}{2}$

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: A.

Ta có: $(\vec{B A}, \vec{B C}) = \hat{A B C}$

Xét tam giác ABC

Áp dụng định lí côsin ta có:

$\cos \hat{A B C} = \frac{B A^{2} + B C^{2} - A C^{2}}{2 B A . B C} = \frac{5^{2} + 4^{2} - 6^{2}}{2.5.4} = \frac{1}{8}$

Vậy $c o s (\vec{B A}, \vec{B C}) = c o s \hat{A B C} = \frac{1}{8}$ .

Câu 6:

Cho tam giác ABC có AB = 12, BC = 15, AC = 13. Tính $c o s (\vec{A B}, \vec{A C})$ .

A. $\frac{1}{39}$

B. $\frac{1}{3}$

C. $\frac{1}{9}$

D. $\frac{11}{39}$

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: D.

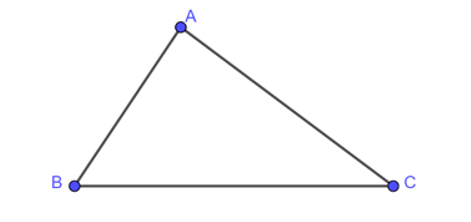
Cho tam giác ABC có AB = 12, BC = 15, AC = 13. Tính cos (vecto AB, vecto AC) (ảnh 1)

Ta có: $(\vec{A B}, \vec{A C}) = \hat{B A C}$

Xét tam giác ABC

Áp dụng định lí côsin ta có:

$\cos \hat{B A C} = \frac{A B^{2} + A C^{2} - B C^{2}}{2 A B . A C} = \frac{12^{2} + 13^{2} - 15^{2}}{2.12.13} = \frac{11}{39}$

Vậy $c o s (\vec{A B}, \vec{A C}) = \frac{11}{39}$ .

Câu 7:

Cho hình vuông ABCD tâm O. Tính $(\vec{C A}, \vec{B A})$ .

A. 90°;

B. 60°;

C. 30°;

D. 45°.

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: D.

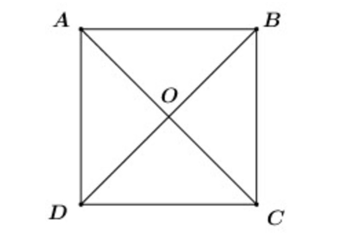
Cho hình vuông ABCD tâm O. Tính (vecto BA, vecto CA) (ảnh 1)

Xét hình vuông ABCD có: $\vec{B A} = \vec{C D}$

Do đó, $(\vec{C A}, \vec{B A}) = (\vec{C A}, \vec{C D}) = \hat{A C D}$

Xét tam giác ACD có:

DA = DC (do ABCD là hình vuông)

$\hat{A D C} = 90 °$

Do đó, tam giác ACD vuông cân tại D.

$\Rightarrow \hat{A C D} = 45 °$

Vậy $(\vec{C A}, \vec{B A}) = 45 °$ .

Câu 8:

Cho hình vuông ABCD tâm O. Tính $(\vec{O A}, \vec{O C})$ .

A. 180°;

B. 0°;

C. 30°;

D. 45°.

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: A.

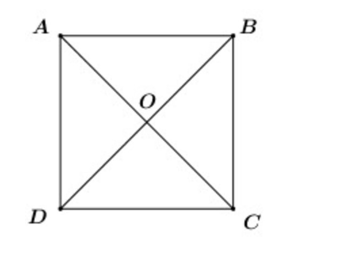
Cho hình vuông ABCD tâm O. Tính (vecto OA, vecto OC) (ảnh 1)

Ta có: $\vec{O A}$ và $\vec{O C}$ là hai vectơ cùng phương, ngược hướng.

Vậy $(\vec{O A}, \vec{O C}) = 180 °$ .

Câu 9:

Cho hình chữ nhật ABCD. Tính góc $(\vec{A B}, \vec{D C})$ .

A. 180°;

B. 0°;

C. 30°;

D. 45°.

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: B.

Do ABCD là hình chữ nhật nên $\vec{A B}, \vec{D C}$ cùng hướng.

Vậy $(\vec{A B}, \vec{D C}) = 0 °$ .

Câu 10:

Cho hình thoi ABCD tâm O. Biết BD = $2 \sqrt{3}$ , AC = 6. Tính $(\vec{B A}, \vec{B C})$ .

A. 180°;

B. 120°;

C. 30°;

D. 65°.

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: B.

Hình thoi ABCD có tâm O nên O là trung điểm của hai đường chéo AC và BD, hơn nữa hai đường chéo này vuông góc với nhau tại O.

Do đó, ta có:

BD = $2 \sqrt{3} \Rightarrow O B = \sqrt{3}$

AC = 6 ⇒ AO = 3.

Xét tam giác AOB vuông tại O có: $\tan \hat{A B O} = \frac{A O}{O B} = \frac{3}{\sqrt{3}} \Rightarrow \hat{A B O} = 60 °$ .

Do ABCD là hình thoi nên BD là tia phân giác góc $\hat{A B C}$ , do đó ta có:

$\hat{A B C} = 2 \hat{A B O} = 2.60 ° = 120 °$ .

Vậy $(\vec{B A}, \vec{B C}) = \hat{A B C} = 120 °$ .

Bắt đầu thi ngay

Trắc nghiệm Toán 10 CTST Bài 4. Tích vô hướng của hai vectơ có đáp án

Dạng 1: Xác định góc giữa hai vectơ có đáp án

Danh sách câu hỏi

Bài thi liên quan

Có thể bạn quan tâm

Các bài thi hot trong chương